fréquence Cumulative
Contenu archivé
L’Information identifiée comme archivée est fournie à des fins de référence, de recherche ou de tenue de documents. Il n’est pas assujetti aux normes Web du gouvernement du Canada et n’a pas été modifié ou mis à jour depuis son archivage. Veuillez nous contacter pour demander un autre format que ceux disponibles.,
- exemple 1 – variables discrètes
- exemple 2 – variables continues
- autres calculs de fréquence cumulative
la fréquence Cumulative est utilisée pour déterminer le nombre d’observations situées au-dessus (ou en dessous) d’une valeur particulière dans un ensemble de données. La fréquence cumulative est calculée à l’aide d’un tableau de répartition des fréquences, qui peut être construit à partir de parcelles de tiges et de feuilles ou directement à partir des données.
la fréquence cumulative est calculée en ajoutant chaque fréquence d’une table de distribution de fréquence à la somme de ses prédécesseurs., La dernière valeur sera toujours égale au total pour toutes les observations, car toutes les fréquences auront déjà été ajoutées au total précédent.
variables discrètes ou continues
Les Variables de tout calcul peuvent être caractérisées par la valeur qui leur est assignée. Une variable discrète est constituée de catégories distinctes et indivisibles. Aucune valeur ne peut exister entre une variable et son voisin. Par exemple, si vous observiez une présence en classe enregistrée au jour le jour, vous découvrirez peut-être que la classe compte 29 étudiants un jour et 30 étudiants un autre., Cependant, il est impossible que la fréquentation des étudiants soit comprise entre 29 et 30. (Il n’y a tout simplement pas de place pour observer des valeurs entre ces deux valeurs, car il n’y a aucun moyen d’avoir 29 étudiants et demi.)
Toutes les variables ne sont pas caractérisées comme discrètes. Certaines variables (telles que le temps, la taille et le poids) ne sont pas limitées à un ensemble fixe de catégories indivisibles. Ces variables sont appelées variables continues, et elles sont divisibles en un nombre infini de valeurs possibles. Par exemple, le temps peut être mesuré en fractions d’heures, minutes, secondes et millisecondes., Donc, au lieu de finir une course en 11 ou 12 minutes, un jockey et son cheval peuvent franchir la ligne d’arrivée en 11 minutes et 43 secondes.
Il est essentiel de connaître la différence entre les deux types de variables afin de calculer correctement leur fréquence cumulée.
exemple 1 – variables discrètes
Le nombre total de grimpeurs de Lake Louise, en Alberta, a été enregistré sur une période de 30 jours. Les résultats sont comme suit:
31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56, 4, 54, 39, 52, 35, 51, 63, 42.,e variables discrètes pour:
- mettre en place un tracé tige et feuille, (voir la section sur les tracés tige et feuille) avec des colonnes supplémentaires étiquetées fréquence, valeur supérieure et Fréquence Cumulative
- déterminer la fréquence des observations pour chaque tige
- trouver la valeur supérieure pour chaque tige
- calculer la fréquence cumulative en ajoutant les nombres dans la colonne Fréquence
- enregistrer tous les résultats dans le tracé
réponses:
- Le nombre d’alpinistes varie de 4 à 65. Afin de produire un tracé de la tige et de la feuille, il est préférable de regrouper les données par intervalles de classe de 10.
chaque intervalle peut être situé dans la colonne de tige. Les nombres dans cette colonne représentent le premier nombre de l’intervalle de classe. (Par exemple, la tige 0 représente l’intervalle 0-9, la tige 1 représente l’intervalle de 10-19, et ainsi de suite.)
la colonne feuille répertorie le nombre d’observations qui se trouvent dans chaque intervalle de classe., Par exemple, dans la tige 2 (intervalle 20-29), les trois observations, 23, 24 et 26, sont représentées par 3, 4 et 6.
la colonne Fréquence répertorie le nombre d’observations trouvées dans un intervalle de classe. Par exemple, dans la tige 5, neuf feuilles (ou observations) ont été trouvées; dans la tige 1, Il n’y en a que deux.
Utilisez la colonne Fréquence pour calculer la fréquence cumulée.
- tout d’abord, ajoutez le numéro de la colonne de fréquence à son prédécesseur. Par exemple, dans la Tige 0, nous n’avons qu’une seule observation et aucun prédécesseurs. La fréquence cumulée est un.,
1 + 0 = 1 - Cependant dans la Tige 1, il y a deux observations. Ajoutez ces deux à la fréquence cumulative précédente (une), et le résultat est trois.
1 + 2 = 3 - Dans la tige 2, Il y a trois observations. Ajoutez ces trois à la fréquence cumulative précédente (trois) et le total (six) est la fréquence cumulative pour le Stim 2.
3 + 3 = 6 - continuez ces calculs jusqu’à ce que vous ayez additionné tous les nombres dans la colonne de fréquence.
- Enregistrez les résultats dans la colonne fréquence Cumulée.,
la colonne Valeur supérieure répertorie l’observation (variable) avec la valeur la plus élevée dans chacun des intervalles de classe. Par exemple, dans le Stim 1, les deux observations 8 et 9 représentent les variables 18 et 19. La valeur supérieure de ces deux variables est 19.
Tableau 1.,>8 9 2 19 1 + 2 = 3 2 3 4 6 3 26 3 + 3 = 6 3 1 5 5 7 9 5 39 6 + 5 = 11 4 0 1 2 3 5 9 6 49 11 + 6 = 17 5 0 1 1 2 4 4 5 6 7 9 57 17 + 9 = 26 6 0 2 3 5 4 65 26 + 4 = 30 - tout d’abord, ajoutez le numéro de la colonne de fréquence à son prédécesseur. Par exemple, dans la Tige 0, nous n’avons qu’une seule observation et aucun prédécesseurs. La fréquence cumulée est un.,
- Since these variables are discrete, use the upper values in plotting the graph., Tracez les points pour former une courbe continue appelée ogive.
Toujours l’étiquette du graphique avec la fréquence cumulée, correspondant au nombre d’observations effectuées sur l’axe vertical.,
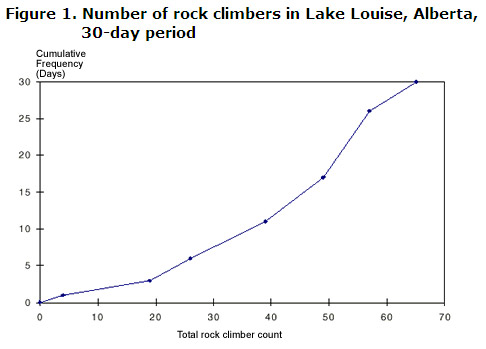
les informations suivantes peuvent être obtenues à partir d’un graphique ou d’un tableau:
- sur 11 des 30 jours, 39 personnes ou moins ont escaladé les rochers autour du Lac Louise
- sur 13 des 30 jours, 50 personnes ou plus ont escaladé les rochers autour de Lake Louise
lorsqu’une variable continue est utilisée, le calcul de la fréquence cumulative et le tracé du graphique nécessitent une approche légèrement différente de celle utilisée pour une variable discrète.,
exemple 2-variables continues
pendant 25 jours, la profondeur de la neige à Whistler Mountain (C.-B.) a été mesurée (au centimètre près) et enregistrée comme suit:
242, 228, 217, 209, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257.,
- utilisez les variables continues ci-dessus pour:
- mettre en place une table de distribution de fréquence
- trouver la fréquence pour chaque intervalle de classe
- localiser le point final pour chaque intervalle de classe
- calculer la fréquence cumulée en ajoutant les nombres dans la colonne de fréquence
- enregistrer tous les résultats dans la table
- utiliser les informations recueillies à partir de la table de distribution de fréquence pour tracer un graphique de fréquence cumulée.
réponses:
- Les mesures de profondeur de neige vont de 209 cm à 266 cm., Afin de produire le tableau de répartition des fréquences, il est préférable de regrouper les données par intervalles de classe de 10 cm chacun.
dans la colonne de profondeur de neige, chaque intervalle de classe de 10 cm de 200 cm à 270 cm est répertorié.
La colonne « Fréquence » enregistre le nombre d’observations qui se situent dans un intervalle particulier. Cette colonne représente les observations dans la colonne Tally, uniquement sous forme numérique.,
la colonne de point de terminaison fonctionne comme la colonne de valeur supérieure de L’Exercice 1, à l’exception que le point de terminaison est le nombre le plus élevé de l’intervalle, quelle que soit la valeur réelle de chaque observation. Par exemple, dans l’intervalle de classe 210-220, la valeur réelle des deux observations est 217 et 219. Mais, au lieu d’utiliser 219, l’extrémité 220 est utilisé.
la colonne Fréquence Cumulative indique le total de chaque fréquence ajoutée à son prédécesseur.
Tableau 2. Profondeur de neige mesurée à Whistler Mountain (C.-B.),e2cd5a9″> 5 240 11 240 to < 250 
7 250 18 250 to < 260 
5 260 23 260 to < 270 
2 270 25 - Because the variable is continuous, the endpoints of each class interval are used in plotting the graph., Les points tracés sont réunis pour former une ogive.
rappelez-vous que la fréquence cumulative (nombre d’observations effectuées) est indiquée sur l’axe y vertical et que toute autre variable (profondeur de neige) est indiquée sur l’axe X horizontal, comme le montre la Figure 2.,

les informations suivantes peuvent être obtenues à partir d’un graphique ou d’un tableau:
- aucun des 25 jours n’avait une profondeur de neige inférieure à 200 cm
- Un des 25 jours de neige avait une profondeur inférieure à 210 cm
- deux des 25 jours de neige avaient une profondeur de 260 cm ou plus
autres calculs de fréquence cumulatifs
un autre calcul qui peut être obtenu à l’aide d’une table de distribution de fréquence est la distribution de fréquence relative. Cette méthode est définie comme le pourcentage d’observations tombant dans chaque intervalle de classe., Fréquence Relative cumulée peut être trouvé en divisant la fréquence de chaque intervalle par le nombre total d’observations. (Pour plus d’informations, voir distribution des fréquences dans le chapitre intitulé Organisation des données.)
une table de répartition des fréquences peut également être utilisée pour calculer le pourcentage cumulatif. Cette méthode de distribution de fréquence nous donne le pourcentage de la fréquence cumulative, par opposition au pourcentage de la fréquence.