The colors of the body of the table illustrate the number of ways to throw each total., La probabilité de lancer un total donné est le nombre de façons de lancer ce total divisé par le nombre total de combinaisons (36). Dans le tableau suivant, le nombre spécifique de façons de lancer chaque total et la probabilité de lancer ce total sont indiqués.

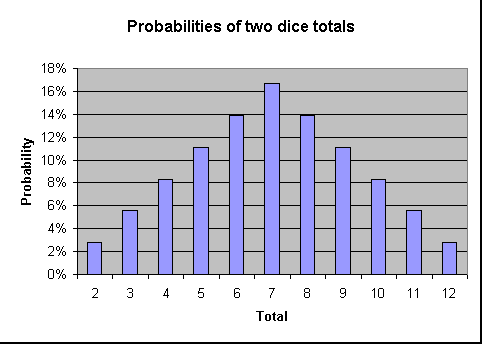
ce qui suit montre la probabilité de lancer chaque total dans un format graphique. Comme le montre le graphique, plus le total est proche de 7, Plus la probabilité qu’il soit jeté est grande.,

L’exemple de pari sur le terrain

maintenant que nous comprenons la probabilité de lancer chaque total, nous pouvons appliquer cette information aux jeux de dés dans les casinos pour calculer le bord de la maison. Par exemple, considérons le pari sur le terrain dans le craps. Ce pari rapporte 1:1 (Argent pair) si le prochain lancer est un 3, 4, 9, 10 ou 11, 2:1 (doubler la mise) sur le 2, et 3:1 (tripler la mise) sur le 12. Notez qu’il y a 7 totaux qui gagnent et seulement 4 qui perdent, ce qui pourrait amener quelqu’un qui ne savait pas mieux à penser que c’était un bon pari.,

le rendement du Joueur peut être défini comme la somme des produits de la probabilité de chaque événement et du rendement net de cet événement. Le tableau suivant montre chaque total possible, le rendement net, la probabilité de lancer ce total et le rendement moyen. Le rendement moyen est le produit du rendement net et la probabilité. Le rendement du Joueur est la somme des rendements moyens.

la dernière ligne montre le retour du joueur à être -.0278, en d’autres termes, pour chaque Pari de 1 bet, le Joueur peut s’attendre à perdre 2,78 cents., La perte du Joueur est le gain de la maison donc l’avantage de la maison est le produit de -1 et le retour du joueur, dans ce cas 0.0278 ou 2.78%.

Pour les probabilités dans la somme de plus de deux dés, veuillez consulter mon probabilités de 1 à 25 dés section.

écrit par: Michael Shackleford