- contexte historique
- Magnitude apparente, m
- Magnitude absolue, m
- trouver la Distance aux étoiles – module de Distance
- calculs de Magnitude/Distance
- nommage& identification des étoiles
étudiez la photographie du champ stellaire ci-dessous. Il montre une région du ciel autour de la constellation Crux, communément appelée La Croix du Sud. Déplacez votre curseur sur la photo pour identifier certaines étoiles.
quelle étoile est la plus brillante?,

Si vous avez répondu Alpha (α) du centaure, l’étoile en bas à gauche de la photo, vous avez raison. Comme vous pouvez le voir, une image photographique comme celle-ci montre beaucoup plus d’étoiles que vous ne pouvez voir avec votre œil nu. Néanmoins, certaines étoiles sont plus proéminentes que d’autres. En choisissant α Centauri, vous avez fait quelques hypothèses. Quels étaient-ils?
Une telle photographie montre des étoiles brillantes comme des disques plus grands que des étoiles plus faibles., Cela signifie-t-il que ces étoiles sont physiquement plus grandes que les étoiles plus faibles sur la photo? Rappelez-vous, dans la section sur l’astrométrie, nous avons appris que toutes les étoiles autres que notre Soleil sont si éloignés qu’ils sont effectivement des sources ponctuelles. Pourquoi alors certains apparaissent-ils plus brillants (à nos yeux) ou plus grands (sur les photographies) que d’autres? Ce qui, en fait, de la luminosité et comment pouvons-nous mesurer? Les réponses à ces questions sont au centre de cette section.,
Contexte Historique

Le concept de mesure et de comparaison de la luminosité des étoiles remonte à L’astronome et mathématicien grec Hipparque (190 – 120 avant JC). L’un des plus grands astronomes de l’antiquité, il est crédité d’avoir produit un catalogue de 850 étoiles avec des positions et des luminosités comparatives., Dans son système, les étoiles les plus brillantes ont reçu une magnitude de 1, la magnitude la plus brillante suivante 2 et ainsi de suite aux étoiles les plus faibles, juste visibles à l’œil nu qui étaient de magnitude 6. Cette échelle de six points peut être considérée comme un classement, les étoiles de premier ordre, les plus brillantes, étaient de première magnitude et les étoiles de faible intensité étaient de sixième magnitude.
la découverte d’étoiles plus faibles avec des télescopes au début des années 1600 a nécessité une extension de l’échelle au-delà de la magnitude 6., Le développement des photomètres visuels, instruments de mesure des intensités stellaires, au XIXe siècle par John Herschel et d’autres a incité les astronomes à adopter une norme internationale. Le fait que les yeux détectent les différences d’intensité logarithmiquement plutôt que linéairement a été découvert dans les années 1830. en 1856 Norman Pogson a proposé qu’une étoile de magnitude 1 était 100 × plus brillante qu’une étoile de magnitude 6. Une différence d’une magnitude était donc égale à 5√100 = 2,512 fois en luminosité.,
Magnitude Apparente m
La magnitude apparente m, d’une étoile, c’est l’ampleur qu’il a vu par un observateur sur la Terre.
un objet très lumineux, comme le soleil ou la Lune, peut avoir une magnitude apparente négative. Bien Qu’Hipparque ait initialement attribué aux étoiles les plus brillantes une magnitude de 1, une comparaison plus minutieuse montre que L’Étoile la plus brillante du ciel nocturne, Sirius ou α Canis Majoris (CMa) a en fait une magnitude apparente de m = -1,44. Avec le recalibrage des valeurs originales D’Hipparque, L’étoile brillante Véga est maintenant définie pour avoir une magnitude apparente de 0,0.,
suite à la découverte télescopique d’étoiles faibles au début des années 1600, l’échelle de magnitude a également dû être étendue aux objets plus faibles que la magnitude 6. Le tableau ci-dessous montre la gamme des magnitudes apparentes pour les objets célestes.
| Objet | Apparentes Grandeur |
|---|---|
| Soleil |
-26.5
|
| Pleine Lune |
-12.5
|
| Vénus |
-4.,3
|
| Mars or Jupiter |
-2
|
| Sirius (α CMa) |
-1.44
|
| Vega (α Lyr) |
0.0
|
| Alnair (α Gru) |
1.73
|
| Naked-eye limit |
6.5
|
| Binocular limit |
10
|
| Proxima Cen |
11.,09
|
| Visual limit through 20 cm telescope |
14
|
| QSO at redshift z = 2 |
≈ 20
|
| Cepheid in galaxy M100 observed with HST |
26
|
| Galaxy at z = 6 observed with Gemini 8.1 m telescope |
28
|
| Limit for James Webb Space Telescope |
≥ 30
|
If a star of magnitude 1 is 2.,512 × plus lumineuse qu’une étoile de magnitude 2 et 100 &fois plus lumineux qu’une sixième étoile de magnitude comment beaucoup plus brillant est-il qu’une étoile de magnitude 3? Vous devez être prudent ici. Ce n’est pas simplement 2 × 2.512 différent. Vous devez vous rappeler qu’une différence d’une ampleur égale à 5√100 = 2.512. Une différence de 2 magnitudes donc = 2.5122 = 6.31 × différence de luminosité.
deux objets de magnitudes différentes varient donc en luminosité de 2,512 élevés à la puissance de la différence de magnitude., Si nous écrivons ceci comme une équation, le rapport de luminosité ou d’intensité, IA / IB entre deux objets, A et B, de magnitudes mA et mB est donné par l’équation suivante:
regardons un exemple.
Exemple 1: Comparaison de deux étoiles.
combien plus lumineux est Alnair, magnitude apparente de +1,73 que Proxima Cen avec une magnitude de 11,09?
en Utilisant l’équation 4.1, nous avons:
donc les remplacer par:
exemple 2: Combien plus lumineux est le Soleil Que La Pleine Lune?
pour cela, nous rappelons dans le tableau ci – dessus que le soleil a une magnitude apparente de -26,5 et La Pleine Lune, – 12,5.
Donc, en utilisant l’équation 4.1, on obtient:
substituant dans nous donne:
Il est important de se rappeler que la magnitude est simplement un nombre, il n’a pas d’unités. Le symbole de la magnitude apparente est un m minuscule; vous devez le préciser dans tout problème.
Magnitude absolue, M
Qu’est-ce que le fait que Sirius ait une magnitude apparente de -1,44 et Bételgeuse une magnitude apparente de 0,45 nous dit de ces deux étoiles? Une autre façon de penser à cela est de demander pourquoi Sirius est-il l’Étoile la plus brillante du ciel nocturne?, Une étoile peut sembler prometteur pour deux raisons principales:
- Il peut être intrinsèquement lumineux, qui est, il peut être un puissant émetteur de rayonnement électromagnétique, ou
- Il peut être très proche de nous, ou les deux.
la magnitude apparente d’une étoile dépend donc en partie de sa distance de nous. En fait Sirius semble plus lumineux que Bételgeuse précisément parce que Sirius est très proche de nous, à seulement 2,6 pc alors que Bételgeuse est distante d’environ 160 pc., La prise de conscience que les étoiles n’ont pas toutes à peu près la même luminosité signifiait que la magnitude apparente seule n’était pas suffisante pour comparer les étoiles. Un nouveau système qui permettrait aux astronomes de comparer directement les étoiles a été développé. Ce système est appelé la magnitude absolue, M.
La magnitude absolue, M, d’une étoile est la magnitude de l’étoile si elle était à une distance de 10 parsecs de nous. Une distance de 10 pc est purement arbitraire mais maintenant internationalement convenue par les astronomes., L’échelle de magnitude absolue est la même que pour la magnitude apparente, c’est une différence de 1 magnitude = 2.512 fois la différence de luminosité. Cette échelle logarithmique est également ouverte et sans unité. Encore une fois, plus la valeur de M est basse ou négative, plus l’étoile est brillante. Magnitude absolue est une façon commode d’exprimer la luminosité d’une étoile. Une fois que la magnitude absolue d’une étoile est connue, vous pouvez également la comparer à d’autres étoiles. Bételgeuse, M = -5,6 est intrinsèquement plus lumineuse que Sirius avec un M = 1,41.
notre Soleil a une magnitude visuelle absolue de 4,8.,
trouver la Distance aux étoiles – module de Distance
comme vous vous en souvenez peut-être dans la section sur l’astrométrie, la plupart des étoiles sont trop éloignées pour que leur parallaxe soit mesurée directement. Néanmoins, si vous connaissez à la fois les magnitudes apparentes et absolues d’une étoile, vous pouvez déterminer sa distance. Regardons à nouveau Sirius et Bételgeuse plus une autre étoile appelée GJ 75.
à quelle distance se trouve GJ 75? C’est une étoile inhabituelle en ce que ses grandeurs apparentes et absolues sont les mêmes. Pourquoi? La raison en est qu’il est en réalité de 10 parsecs de nous, donc, par définition, ses deux grandeurs doivent être les mêmes.,
Qu’en est-il de Sirius? Sa magnitude apparente est plus faible (donc plus brillante) que sa magnitude absolue. Cela signifie qu’il est plus proche de 10 parsecs de nous. La magnitude apparente de Bételgeuse est plus élevée (donc plus faible) que sa magnitude absolue, de sorte qu’elle apparaîtrait encore plus brillante dans le ciel nocturne si elle n’était distante que de 10 parsecs.
Les astronomes utilisent la différence entre la magnitude apparente et la magnitude absolue, le module de distance, comme moyen de dénommer la distance à une étoile.
- module de Distance = m – M.
- le module de Distance est négatif pour les étoiles plus proches de 10 parsecs.,
- Le module de Distance est positif pour les étoiles situées plus loin que 10 parsecs.
- La Taille du module de distance détermine la valeur réelle de la distance, de sorte qu’une étoile de module de distance 1.5 est plus proche d’une étoile avec un module de distance de 8.7.
calculs de Magnitude/Distance
le module de distance peut être utilisé pour déterminer la distance à une étoile en utilisant l’équation:
où d est en parsecs. Notez que si d = 10 pc alors m et M sont les mêmes. (Une dérivation formelle de cette équation est donnée dans la page suivante sur la luminosité)., La feuille de formule du programme NSW HSC fournit l’équation comme suit:
mais il s’agit simplement d’un remaniement de l’équation 4.2. Vous devriez être à l’aise dans la résolution de cette équation étant donné deux des trois variables. Faites – nous savoir regardez comment vous pouvez résoudre quelques exemples.
exemple 3: étant donné m et d, il faut trouver M.
β Crucis (ou Mimosa) a une magnitude apparente de 1,25 et est distante de 108 parsecs. Quelle est sa magnitude absolue?
en Utilisant l’équation 4.3, nous avons:
donc β Crucis a une magnitude absolue de -3.92
Note Ce calcul a montré un fonctionnement complet de sorte que chaque étape est explicite. (Rappelez-vous dans la résolution des équations de magnitude log se réfère aux logarithmes à la base 10 et non aux logarithmes naturels ou ln.)
exemple 4: étant donné m et M, trouver D.
Bételgeuse a une magnitude apparente de 0,45 et une magnitude absolue de -5,14. À quelle distance est-il?
Ce problème nous oblige à réécrire l’équation 4.2 pour nous donner d comme l’inconnu., Ceci est illustré ci-dessous:
ce qui peut être écrit comme:
maintenant remplacer par:
donc, Bételgeuse est d’environ 130 pc distant.
encore une fois, cet exemple montre un travail complet alors qu’en réalité, vous ne pouvez pas montrer chaque étape., Il est important, cependant, que vous définissez votre travail sur de tels problèmes clairement afin que vous puissiez vérifier votre manipulation algébrique et vos substitutions. Travailler avec des journaux et des index peut être délicat, alors assurez-vous de savoir comment les faire sur votre calculatrice.
exemple 5: étant donné M et d, Trouver M.
en pratique ce type de problème est moins réaliste pour les objets réels car nous pouvons normalement mesurer directement leurs magnitudes apparentes mais il se peut que nous souhaitions calculer quelle magnitude apparente une classe ou un type d’objet peut avoir donné les autres paramètres. Encore une fois, en commençant par l’équation 4.,3 déterminons à quel point une supergéante telle que Deneb avec une magnitude absolue de -8,73 apparaîtrait si elle était à 230 parsecs.
donc les remplacer par:
donc Deneb aurait une magnitude apparente de -1.89. Cela le rendrait plus lumineux dans notre ciel nocturne que Sirius (m = -1,44)., En réalité Deneb est distant d’environ 990 pc bien que cette valeur ait une grande incertitude.
exemple 6: et si d n’est pas donné mais parallaxe, p est donné?
C’est en fait très simple. Rappelez-vous de la section sur l’astrométrie qu’il existe une relation directe entre la distance et la parallaxe.
il vous suffit d’insérer cela dans l’équation 4.2 ou 4.3.
nommage& identification des étoiles
laissez-nous savoir revisiter cette photo de Crux et les pointeurs en haut de cette page., La photo ci-dessous montre la même région avec les étoiles proéminentes étiquetées. Ils ont également leurs magnitudes apparentes montrées. Crux est une constellation, l’une des 88 régions dans lesquelles la sphère céleste a été divisée et convenue internationalement par les astronomes. Crux est en fait la plus petite des constellations et est facilement identifiée dans le ciel du Sud. Les étoiles proéminentes à proximité communément appelées les pointeurs font en fait partie d’une grande constellation appelée Centaure.

Maintenant, vous remarquerez peut-être que les étoiles sont nommées en utilisant des lettres de l’alphabet grec; α, β, γ δ Et ε (alpha, bêta, gamma, delta, epsilon étant les cinq premières) suivies de l’abréviation standard de trois lettres pour chaque constellation (Cru pour Crucis ou Crux et Cen pour Centaurus). Si vous regardez attentivement les magnitudes apparentes des cinq étoiles nommées dans Crux, vous verrez que l’Étoile la plus brillante est étiquetée α, la prochaine β et ainsi de suite., Ce système est appelé le système Bayer, d’après Johann Bayer qui l’a introduit en 1603. L’Étoile la plus brillante d’une constellation se voit attribuer la lettre α, la prochaine β et ainsi de suite. Une exception à cette règle est & alpha Orionis ou Betelgeuse. Il est en fait plus faible que β Ori, Rigel par une petite quantité. C’est un cas historique intéressant résolu par la réalisation que Bételgeuse a légèrement diminué en luminosité depuis qu’il a été nommé sous le système Bayer.,
un point à retenir sur les constellations est que les étoiles dans une constellation ne sont généralement pas physiquement associées les unes aux autres, contrairement aux étoiles dans les amas. Le fait que apparaissent rapprochés est purement un effet d’alignement le long de la ligne de visée du tour. En fait, les étoiles dans la région ci-dessus sont largement séparées en distance de nous comme indiqué dans l’image suivante.
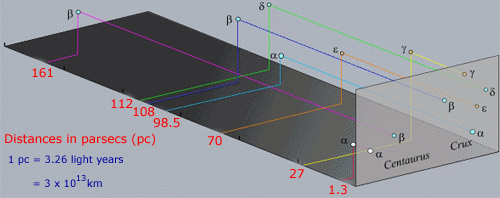
certaines des étoiles brillantes telles que α Cen ont également leur propre nom spécifique. SIRIUS (α Sco) est l’un de ces exemples tandis que α Cen est également appelé Rigel Kentaurus. De nombreux noms d’étoiles sont d’origine arabe à partir de l’époque où les enregistrements Grecs ont été préservés et développés par les astronomes islamiques. Le problème avec le système Bayer de nommer les étoiles est qu’il n’y a que 24 lettres dans l’alphabet grec, mais il y a beaucoup plus d’étoiles que dans chaque constellation.
en fait, la plupart des étoiles n’ont pas de nom spécifique ni de classification Bayer., De nos jours, les astronomes ont compilé de vastes catalogues d’étoiles, certains avec plus de 10 millions d’objets, de sorte que la plupart des étoiles n’ont qu’un numéro de catalogue. Les étoiles peuvent avoir plus d’un nom d’identification ou d’un numéro de catalogue, selon le nombre de catalogues dans lesquels elles se trouvent. L’étoile variable, δ Cep par exemple est également connue sous le nom de HIP 110991, SAO 34508, ou l’un des plus de 30 autres identifiants! De nombreux catalogues utilisent des coordonnées célestes telles que L’Ascension droite et la déclinaison pour identifier les objets. Ainsi δ Cep est connu comme ira 22273+5809, CCDM J22292+5825a et AAVSO 2225 + 57., Les légères variations de RA et de dec pour les catalogues sont dues au mouvement propre des étoiles et à la précession du référentiel.