The colors of the body of the table illustrate the number of ways to throw each total., La probabilidad de lanzar un total dado es el número de formas de lanzar ese total dividido por el número total de combinaciones (36). En la siguiente tabla se muestra el número específico de formas de lanzar cada total y la probabilidad de lanzar ese total.

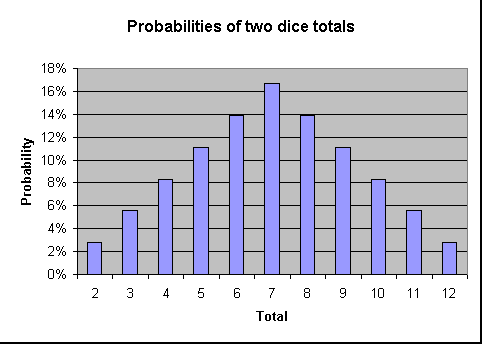
lo siguiente muestra la probabilidad de lanzar cada total en un formato de gráfico. Como muestra el gráfico, cuanto más cerca esté el total de 7, mayor será la probabilidad de que se lance.,

El Ejemplo de Apuesta de campo

ahora que entendemos la probabilidad de lanzar cada total podemos aplicar esta información a los juegos de dados en los casinos para calcular la ventaja de la casa. Por ejemplo, considere la apuesta de campo en el juego de dados. Esta apuesta paga 1:1 (Dinero par) si el siguiente lanzamiento es un 3, 4, 9, 10 o 11, 2:1 (el doble de la apuesta) en el 2, y 3:1 (el triple de la apuesta) en el 12. Tenga en cuenta que hay 7 totales que ganan y solo 4 que pierden, lo que podría hacer que alguien que no sabía mejor que pensar que era una buena apuesta.,

El retorno del jugador se puede definir como la suma de los productos de la probabilidad de cada evento y el retorno neto de ese evento. La siguiente tabla muestra cada total posible, el retorno neto, la probabilidad de lanzar ese total y el retorno promedio. El retorno promedio es el producto del retorno neto y la probabilidad. El retorno del jugador es la suma de los retornos promedio.

la última fila muestra el retorno del jugador a ser -.0278, en otras palabras, por cada bet 1 Apuesta el Jugador puede esperar perder 2,78 centavos., La pérdida del jugador es la ganancia de la casa por lo que la ventaja de la casa es el producto de -1 y el retorno del jugador, en este caso 0.0278 o 2.78%.

para las probabilidades en la suma de más de dos dados por favor vea mi probabilidades para 1 a 25 dados sección.escrito por: Michael Shackleford