la Prueba de Hipótesis
 El objetivo principal de la estadística es la prueba de una hipótesis. Por ejemplo, puede realizar un experimento y descubrir que cierto medicamento es efectivo para tratar los dolores de cabeza. Pero si no puedes repetir ese experimento, nadie tomará en serio tus resultados. Un buen ejemplo de esto fue el descubrimiento de la fusión fría, que quedó en la oscuridad porque nadie fue capaz de duplicar los resultados.,
El objetivo principal de la estadística es la prueba de una hipótesis. Por ejemplo, puede realizar un experimento y descubrir que cierto medicamento es efectivo para tratar los dolores de cabeza. Pero si no puedes repetir ese experimento, nadie tomará en serio tus resultados. Un buen ejemplo de esto fue el descubrimiento de la fusión fría, que quedó en la oscuridad porque nadie fue capaz de duplicar los resultados.,
vea el video para una breve descripción de las pruebas de hipótesis, o siga leyendo a continuación:
contenido (clic para saltar a la sección):
- ¿Qué es una hipótesis?
- ¿Qué es la Prueba de Hipótesis?
- Ejemplos de pruebas de hipótesis (una prueba Z de muestra).
- prueba de hipótesis sobre una media (TI 83).
- prueba de hipótesis Bayesiana.
- Más Artículos de prueba de hipótesis
Ver también:
- pruebas de hipótesis en una imagen
- valores críticos
- ¿Qué es la hipótesis nula?,
¿necesita ayuda con un problema con la tarea? Echa un vistazo a nuestra página de tutoría!
¿Qué es una Hipótesis?

Andreas Cellarius hipótesis, mostrando los movimientos planetarios.
Una hipótesis es una suposición educada sobre algo en el mundo que te rodea. Debe ser comprobable, ya sea por experimento u observación. Por ejemplo:
- Un nuevo medicamento que usted cree que podría funcionar.
- Una forma de enseñar que crees que podría ser mejor.,
- Una posible localización de nuevas especies.
- Una forma más justa de administrar pruebas estandarizadas.
realmente puede ser cualquier cosa, siempre y cuando se puede poner a prueba.
¿qué es una declaración de hipótesis?
si vas a proponer una hipótesis, es costumbre escribir una declaración. Su declaración se verá así:
«Si yo do(hacer esto a una variable independiente)….entonces (esto le sucederá a la variable dependiente).»
por ejemplo:
- Si I (disminuye la cantidad de agua dada a las hierbas) entonces (las hierbas aumentarán de tamaño).,
- Si yo (dar asesoramiento a los pacientes, además de la medicación) entonces (su escala general de depresión disminuirá).
- Si yo (doy exámenes al mediodía en lugar de 7) Entonces (los resultados de las pruebas de los estudiantes mejorarán).
- Si yo (miro en esta cierta ubicación) entonces (tengo más probabilidades de encontrar nuevas especies).
una buena declaración de hipótesis debe:
- incluir una declaración «si» y «entonces» (de acuerdo con la Universidad de California).
- Incluye tanto las variables independientes y dependientes.
- ser comprobable por experimento, encuesta u otra técnica científicamente sólida.,
- basarse en información de investigaciones previas (ya sea suya o de otra persona).
- Tener criterios de diseño (para proyectos de ingeniería o programación).
¿qué es la prueba de hipótesis?

La prueba de hipótesis en estadísticas es una forma de probar los resultados de una encuesta o experimento para ver si tiene resultados significativos. Básicamente estás probando si tus resultados son válidos al averiguar las probabilidades de que tus resultados hayan ocurrido por casualidad., Si sus resultados pueden haber ocurrido por casualidad, el experimento no será repetible y por lo tanto tiene poco uso.
la prueba de hipótesis puede ser uno de los aspectos más confusos para los estudiantes, principalmente porque antes de que pueda realizar una prueba, debe saber cuál es su hipótesis nula. A menudo, esos problemas verbales difíciles con los que se enfrenta pueden ser difíciles de descifrar., Pero es más fácil de lo que crees; todo lo que necesitas hacer es:
- averiguar tu hipótesis nula,
- declarar tu hipótesis nula,
- Elegir qué tipo de prueba necesitas realizar,
- apoyar o rechazar la hipótesis nula.
¿qué es la hipótesis nula?
Si se remonta la historia de la ciencia, la hipótesis nula es siempre el hecho aceptado. Ejemplos simples de hipótesis nulas que son generalmente aceptadas como verdaderas son:
- El ADN tiene la forma de una doble hélice.
- Hay 8 planetas en el sistema solar (excluyendo Plutón).,
- Tomar Vioxx puede aumentar su riesgo de problemas cardíacos (un medicamento que ahora se retira del mercado).
¿cómo declaro la hipótesis nula?
usted no tendrá que realizar realmente un experimento real o encuesta en las estadísticas elementales (o incluso refutar un hecho como «Plutón es un planeta»!), por lo que se le dará problemas de palabras de situaciones de la vida real. Tendrás que averiguar cuál es tu hipótesis a partir del problema. Esto puede ser un poco más complicado que simplemente averiguar cuál es el hecho aceptado. Con problemas de palabras, usted está buscando encontrar un hecho que es nulificable (i. e., algo que puedes rechazar).
ejemplos de prueba de hipótesis #1: Ejemplo básico
Un investigador piensa que si los pacientes de cirugía de rodilla van a fisioterapia dos veces por semana (en lugar de 3 veces), su período de recuperación será más largo. El tiempo promedio de recuperación para los pacientes de cirugía de rodilla es de 8,2 semanas.
la afirmación de hipótesis en esta pregunta es que el investigador cree que el tiempo promedio de recuperación es superior a 8,2 semanas. Se puede escribir en términos matemáticos como:
H1: μ > 8.,2
a continuación, tendrás que declarar la hipótesis nula (ver: cómo declarar la hipótesis nula). Eso es lo que sucederá si el investigador se equivoca. En el ejemplo anterior, si el investigador está equivocado, entonces el tiempo de recuperación es menor o igual a 8.2 semanas. En matemáticas, eso es:
H0 μ ≤ 8.2
rechazando la hipótesis nula
hace unos diez años, creíamos que había 9 planetas en el sistema solar. Plutón fue degradado como planeta en 2006. La hipótesis nula de «Plutón es un planeta» fue reemplazado por «Plutón no es un planeta.,»Por supuesto, rechazar la hipótesis nula no siempre es tan fácil – la parte difícil suele ser averiguar cuál es tu hipótesis nula en primer lugar.
ejemplos de pruebas de hipótesis (una prueba Z de muestra)
la prueba Z de una muestra no se usa muy a menudo (porque rara vez conocemos la desviación estándar real de la población). Sin embargo, es una buena idea entender cómo funciona, ya que es una de las pruebas más simples que puede realizar en las pruebas de hipótesis., En la clase de Inglés tienes que aprender los conceptos básicos (como gramática y ortografía) antes de poder escribir una historia; piensa en un ejemplo de pruebas z como la base para comprender pruebas de hipótesis más complejas. Esta página contiene dos ejemplos de pruebas de hipótesis para una prueba Z de muestra.
una muestra de ejemplos de pruebas de hipótesis: #2
Un director de cierta escuela afirma que los estudiantes de su escuela están por encima de la inteligencia promedio. Una muestra aleatoria de treinta estudiantes puntajes de CI tienen una puntuación media de 112., ¿Hay suficiente evidencia para apoyar la reclamación del principal? El coeficiente intelectual medio de la población es de 100 con una desviación estándar de 15.
Paso 1: declare la hipótesis nula. El hecho aceptado es que la media de la población es de 100, por lo que: H0: μ=100.
Paso 2: indique la hipótesis alternativa. La afirmación es que los estudiantes tienen puntajes de CI superiores al Promedio, por lo que:
H1: μ > 100.
el hecho de que estamos buscando puntuaciones «mayores que» un cierto punto significa que esta es una prueba de una sola cola.
Paso 3: dibuja un dibujo para ayudarte a visualizar el problema.,
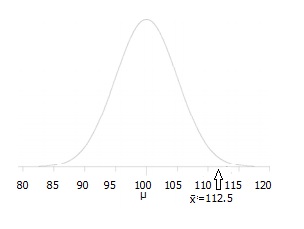
Paso 4: indique el nivel alfa. Si no se le da un nivel alfa, use 5% (0.05).
Paso 5: Buscar el rechazo de la región (dado por su nivel alfa arriba) de la z-tabla. Un área de .05 es igual a una puntuación z de 1.645.
Paso 6: encuentre la estadística de prueba usando esta fórmula: 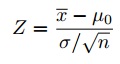
para este conjunto de datos: z= (112.5 – 100) / (15/√30) = 4.56.
Paso 6: Si El Paso 6 es mayor que el paso 5, rechace la hipótesis nula., Si es menor que el paso 5, no puede rechazar la hipótesis nula. En este caso, es mayor (4.56 > 1.645), por lo que puede rechazar el null.
una muestra de ejemplos de pruebas de hipótesis: #3
los niveles de glucosa en sangre para pacientes obesos tienen una media de 100 con una desviación estándar de 15. Un investigador piensa que una dieta alta en almidón de maíz crudo tendrá un efecto positivo o negativo en los niveles de glucosa en sangre., Una muestra de 30 pacientes que han probado la dieta de almidón de maíz crudo tiene un nivel medio de glucosa de 140. Pruebe la hipótesis de que la maicena cruda tuvo un efecto.
*este proceso se hace mucho más fácil si utiliza un TI – 83 o Excel para calcular la puntuación z (el»valor crítico»).,
ver:
- valor crítico Z TI 83
- puntuación Z en Excel
prueba de hipótesis ejemplos: Media (usando TI 83)
puede usar la calculadora TI 83 para la prueba de hipótesis, pero la calculadora no averiguará las hipótesis nulas y alternativas; depende de usted leer la pregunta e ingresarla en la calculadora.
problema de ejemplo: una muestra de 200 personas tiene una edad media de 21 años con una desviación estándar poblacional (σ) de 5. Pruebe la hipótesis de que la media de la población es de 18,9 a α = 0,05.
Paso 1: declare la hipótesis nula., En este caso, la hipótesis nula es que la media de la población es 18.9, por lo que escribimos:
H0: μ = 18.9
Paso 2: Establecer la hipótesis alternativa. Queremos saber si nuestra muestra, que tiene una media de 21 en lugar de 18.9, es realmente diferente de la población, por lo tanto nuestra hipótesis alternativa:
h1: μ ≠ 18.9
Paso 3: Presione Stat y luego presione la flecha derecha dos veces para seleccionar las pruebas.
Paso 4: Pulse 1 para seleccionar 1: Z-Test…. Pulse Intro.
Paso 5: Usa la flecha derecha para seleccionar estadísticas.
Paso 6: Introduzca los datos del problema:
μ0: 18.,9
σ: 5
x: 21
n: 200
μ: ≠μ0
Paso 7: flecha hacia abajo para calcular y pulse Intro. La calculadora muestra el valor de p:
p = 2.87 × 10-9
esto es más pequeño que nuestro valor alfa de.05. Eso significa que debemos rechazar la hipótesis nula.
prueba de hipótesis Bayesiana: ¿Qué es?
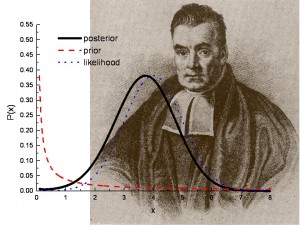
imagen: Los Alamos National Lab.
Las pruebas de hipótesis Bayesianas ayudan a responder la pregunta: ¿se pueden repetir los resultados de una prueba o encuesta? ¿por qué nos importa si una prueba se puede repetir?, Digamos que veinte personas en el mismo pueblo enfermaron de leucemia. Un grupo de investigadores encuentra que las torres de telefonía celular son las culpables. Sin embargo, un segundo estudio encontró que las torres de telefonía celular no tenían nada que ver con el cúmulo de cáncer en el pueblo. De hecho, encontraron que los cánceres eran completamente aleatorios. Si eso suena imposible, ¡realmente puede suceder! Los grupos de cáncer pueden ocurrir simplemente por casualidad. Podría haber muchas razones por las que el primer estudio fue defectuoso., Una de las razones principales podría ser que simplemente no tuvieron en cuenta que a veces las cosas suceden al azar y simplemente no sabemos por qué.
valores de P.
es una buena ciencia informar a las personas si los resultados de tu estudio son sólidos o si podrían haber ocurrido por casualidad. La forma habitual de hacer esto es probar sus resultados con un valor p. Un valor p es un número que se obtiene ejecutando una prueba de hipótesis en sus datos. Un valor de P de 0.05 (5%) o menos suele ser suficiente para afirmar que sus resultados son repetibles., Sin embargo, hay otra manera de probar la validez de sus resultados: pruebas de hipótesis Bayesianas. Este tipo de pruebas le da otra manera de probar la fuerza de sus resultados.
prueba de hipótesis Bayesiana.
las pruebas tradicionales (el tipo que probablemente encontró en elementary stats o AP stats) se llaman No Bayesianas. Se trata de la frecuencia con la que ocurre un resultado durante las repeticiones del experimento. Es una visión objetiva de si un experimento es repetible.la prueba de hipótesis Bayesiana es una visión subjetiva de la misma cosa., Toma en cuenta cuánta fe tienes en tus resultados. En otras palabras, ¿apostaría dinero en el resultado de su experimento?
diferencias entre las pruebas de hipótesis tradicionales y Bayesianas.
la prueba tradicional (no Bayesiana) requiere repetir el muestreo una y otra vez, mientras que la prueba Bayesiana no lo hace. La principal diferencia entre los dos está en el primer paso de la prueba: indicando un modelo de probabilidad. En Bayesian testing agregas conocimientos previos a este paso., También requiere el uso de una probabilidad posterior, que es la probabilidad condicional dada a un evento aleatorio después de que se considere toda la evidencia.
argumentos para pruebas Bayesianas.
muchos investigadores piensan que es una mejor alternativa a las pruebas tradicionales, porque:
- Incluye conocimiento previo sobre los datos.
- Tiene en cuenta las creencias personales sobre los resultados.
Argumentos en contra.
- incluir datos o conocimientos previos no es justificable.
- Es difícil de calcular en comparación con las pruebas no Bayesianas.,
volver al principio
artículos de prueba de hipótesis
Fundamentos:
- ¿Qué es la prueba Ad Hoc?
- prueba de hipótesis compuesta
- ¿Qué es una región de rechazo?
- ¿Qué es una prueba de dos colas?
- ¿Cómo Decidir si una Prueba de Hipótesis es una Cola o de Dos Colas Prueba.
- Cómo decidir si una hipótesis es una prueba de cola izquierda o una prueba de cola derecha.
- Cómo establecer la hipótesis nula en las estadísticas.
- ¿Cómo Encontrar un Valor Crítico.
- Cómo Apoyar o Rechazar una Hipótesis Nula.,
pruebas específicas:
- ANOVA.
- prueba de Brunner Munzel (prueba generalizada de Wilcoxon)
- prueba de Chi cuadrado para la normalidad
- prueba de Cochran-Mantel-Haenszel
- prueba F
- prueba de causalidad de Granger.
- T-Squared de Hotelling
- prueba KPSS.
- ¿Qué es una prueba de Relación de verosimilitud?
- Log rank test.
- MANCOVA
- Secuencial Ratio de Probabilidad de la Prueba
- Cómo Ejecutar una Prueba del Signo.
- T Test: una muestra.
- T-Test: dos muestras.
- Welch’s ANOVA.
- prueba de Welch para varianzas desiguales.,
- Z-Test: una muestra.
- prueba Z: dos proporciones
- prueba Wald.
- ¿Qué es una Aceptación de la Región?
- Cómo calcular el Teorema de Chebyshev.
- Regla de Decisión.
- Grados de Libertad.
- Direccional de Prueba
- False Discovery Rate
- Cómo calcular la Diferencia mínima Significativa.
- niveles en Estadísticas.
- Cómo Calcular el Margen de Error.
- Diferencia de medias (Diferencia de medias)
- Las Múltiples Pruebas Problema.
- ¿Qué es el lema Neyman-Pearson?
- Una prueba de mediana de muestra.,
- REGWF
- Cómo encontrar un tamaño de muestra (Instrucciones generales).
- sig 2(Cola) significado en los resultados
- ¿Qué es una estadística de prueba estandarizada?
- Cómo encontrar el Error estándar
- Valores estandarizados: ejemplo.
- Cómo calcular un T-Score.
- T-Score Vs. A Z. Score.
- probando una media única.
- tamaños de muestra desiguales.
- uniformemente las pruebas más potentes.
- Cómo calcular una puntuación Z.
——————————————————————————
Necesito ayuda con una tarea o cuestión de prueba?, Con Chegg Study, puede obtener soluciones paso a paso a sus preguntas de un experto en el campo. ¡Tus primeros 30 minutos con un tutor de Chegg son GRATIS!