Einführung
Bevor Sie ein Würfelspiel spielen, ist es gut, die Wahrscheinlichkeit einer bestimmten Summe zu kennen. Schauen wir uns zunächst die Möglichkeiten der insgesamt zwei Würfel an. Die folgende Tabelle zeigt die sechs Möglichkeiten für Würfel 1 entlang der linken Spalte und die sechs Möglichkeiten für Würfel 2 entlang der oberen Spalte. Der Körper der Tabelle zeigt die Summe von sterben 1 und sterben 2.,0
The colors of the body of the table illustrate the number of ways to throw each total., Die Wahrscheinlichkeit, eine bestimmte Summe zu werfen, ist die Anzahl der Möglichkeiten, diese Summe dividiert durch die Gesamtzahl der Kombinationen (36) zu werfen. In der folgenden Tabelle wird die spezifische Anzahl der Möglichkeiten, jede Summe zu werfen, und die Wahrscheinlichkeit, diese Summe zu werfen, angezeigt.
Das Folgende zeigt die Wahrscheinlichkeit, jede Summe in einem Diagrammformat zu werfen. Wie das Diagramm zeigt, ist die Wahrscheinlichkeit, dass es geworfen wird, umso größer, je näher die Summe an 7 ist.,
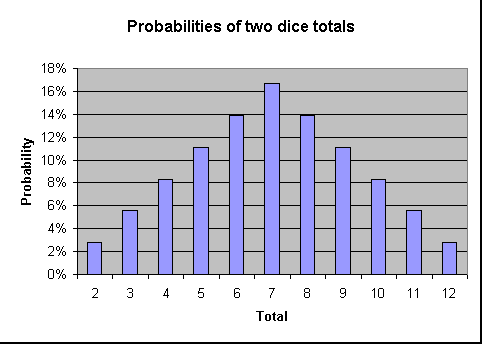
Das Feld Wette Beispiel
Nun, da wir die Wahrscheinlichkeit verstehen, jede Summe zu werfen, können wir diese Informationen auf die Würfelspiele in den Casinos anwenden, um den Hausvorteil zu berechnen. Zum Beispiel betrachten Sie das Feld Wette in Craps. Diese Wette zahlt 1:1 (auch Geld), wenn der nächste Wurf ist ein 3, 4, 9, 10, oder 11, 2:1 (verdoppeln Sie den Einsatz) auf dem 2, und 3:1 (verdreifachen Sie den Einsatz) auf dem 12. Beachten Sie, dass es 7 Summen gibt, die gewinnen und nur 4, die verlieren, was dazu führen kann, dass jemand, der es nicht besser wusste, denkt, dass es ein gutes Glücksspiel war.,
Die Rendite des Spielers kann als Summe der Produkte der Wahrscheinlichkeit jedes Ereignisses und der Nettorendite dieses Ereignisses definiert werden. Die folgende Tabelle zeigt jede mögliche Summe, die Nettorendite, die Wahrscheinlichkeit, diese Summe zu werfen, und die durchschnittliche Rendite. Die durchschnittliche Rendite ist das Produkt der Nettorendite und der Wahrscheinlichkeit. Die Rendite des Spielers ist die Summe der durchschnittlichen Renditen.
Die letzte Zeile zeigt die Rückkehr des Spielers zu sein -.0278, mit anderen Worten, für jede $1 Wette kann der Spieler erwarten 2.78 Cent zu verlieren., Der Verlust des Spielers ist der Gewinn des Hauses, also ist der Hausvorteil das Produkt von -1 und die Rückkehr des Spielers, in diesem Fall 0.0278 oder 2.78%.
Für die Wahrscheinlichkeiten in der Summe von mehr als zwei Würfeln siehe meine Wahrscheinlichkeiten für 1 bis 25 Würfel Abschnitt.
Geschrieben von: Michael Shackleford