Hypothesentests

Der Hauptzweck der Statistik besteht darin, eine Hypothese zu testen. Zum Beispiel könnten Sie ein Experiment durchführen und feststellen, dass ein bestimmtes Medikament bei der Behandlung von Kopfschmerzen wirksam ist. Aber wenn Sie dieses Experiment nicht wiederholen können, wird niemand Ihre Ergebnisse ernst nehmen. Ein gutes Beispiel dafür war die Entdeckung der kalten Fusion, die ins Unklare geriet, weil niemand die Ergebnisse duplizieren konnte.,

Sehen Sie sich das Video an, um einen kurzen Überblick über Hypothesentests zu erhalten, oder lesen Sie weiter unten:

Inhalt (Klicken Sie auf den Abschnitt zu überspringen):

1. Was ist eine Hypothese?
2. Was ist Hypothesentests?
3. Beispiele für Hypothesentests (eine Probe Z-Test).
4. Hypothesentest an einem Mittelwert (TI 83).
5. Bayes-Hypothese zu Testen.
6. Weitere Artikel zum Testen von Hypothesen

Siehe auch:

• Hypothesentests in einem Bild
• Kritische Werte
• Was ist die Nullhypothese?,

Benötigen Sie Hilfe bei Hausaufgaben? Schauen Sie sich unsere Nachhilfe-Seite!

Was ist eine Hypothese?

Eine Hypothese ist eine fundierte Vermutung über etwas in der Welt um dich herum. Es sollte testbar sein, entweder durch Experiment oder Beobachtung. Zum Beispiel:

• Ein neues Medikament, von dem Sie denken, dass es funktionieren könnte.
• Eine Art zu lehren, die Sie denken, könnte besser sein.,
• Ein möglicher Standort neuer Arten.
• Eine gerechtere Art, standardisierte Tests durchzuführen.

Es kann wirklich alles sein, solange Sie es auf die Probe stellen können.

Was ist eine Hypothese Aussage?

Wenn Sie eine Hypothese vorschlagen, ist es üblich, eine Aussage zu schreiben. Ihre Aussage wird wie folgt aussehen:
“ Wenn ich…(tun Sie dies zu einer unabhängigen Variablen)….dann (dies geschieht mit der abhängigen Variablen).“
Zum Beispiel:

• Wenn ich (verringere die Menge an Wasser, die Kräutern gegeben wird)dann (die Kräuter werden größer).,
• Wenn ich (Patienten zusätzlich zu Medikamenten beraten) dann (ihre Gesamtdepressionsskala wird abnehmen).
• Wenn ich (geben Prüfungen am Mittag statt 7) dann (Student Testergebnisse verbessern).
• Wenn ich (schau an diesem bestimmten Ort) dann (ich finde eher neue Arten).

Eine gute Hypothesenaussage sollte:

• eine „if“ – und „then“ – Anweisung enthalten (laut der University of California).
• Enthält sowohl die unabhängigen als auch die abhängigen Variablen.
• testbar durch Experiment, Umfrage oder andere wissenschaftlich fundierte Technik.,
• basiert auf Informationen, die in der Forschung vor (entweder Ihre eigenen oder jemand anderes).
• Haben design kriterien (für engineering oder programmierung projekte).

Was ist Hypothesentests?

Hypothesentests in Statistiken sind eine Möglichkeit für Sie, die Ergebnisse einer Umfrage oder eines Experiments zu testen, um festzustellen, ob Sie aussagekräftige Ergebnisse haben. Sie testen im Grunde, ob Ihre Ergebnisse gültig sind, indem Sie die Wahrscheinlichkeit herausfinden, dass Ihre Ergebnisse zufällig aufgetreten sind., Wenn Ihre Ergebnisse zufällig aufgetreten sind, ist das Experiment nicht wiederholbar und hat daher wenig Nutzen.

Hypothesentests können für Schüler einer der verwirrendsten Aspekte sein, vor allem, weil Sie wissen müssen, was Ihre Nullhypothese ist, bevor Sie überhaupt einen Test durchführen können. Oft können diese kniffligen Wortprobleme, mit denen Sie konfrontiert sind, schwer zu entziffern sein., Aber es ist einfacher als Sie denken; Alles, was Sie tun müssen, ist:

1. Finden Sie Ihre Nullhypothese heraus,
2. Geben Sie Ihre Nullhypothese an,
3. Wählen Sie aus, welche Art von Test Sie durchführen müssen,
4. Unterstützen oder lehnen Sie die Nullhypothese ab.

Was ist die Nullhypothese?

Wenn Sie die Geschichte der Wissenschaft zurückverfolgen, ist die Nullhypothese immer die akzeptierte Tatsache. Einfache Beispiele für Nullhypothesen, die allgemein als wahr akzeptiert werden, sind:

1. DNA ist wie eine Doppelhelix geformt.
2. Es gibt 8 Planeten im Sonnensystem (außer Pluto).,
3. Die Einnahme von Vioxx kann das Risiko von Herzproblemen erhöhen (ein Medikament, das jetzt vom Markt genommen wird).

Wie gebe ich die Nullhypothese an?

Sie sind nicht verpflichtet, tatsächlich führen Sie ein echtes experiment oder eine Umfrage in der elementaren Statistik (oder auch zu widerlegen, eine Tatsache wie „Pluto ist ein planet“!), so dass Sie Wortprobleme aus realen Situationen erhalten. Sie müssen herausfinden, was Ihre Hypothese von dem Problem ist. Dies kann etwas schwieriger sein, als nur herauszufinden, was die akzeptierte Tatsache ist. Bei Wortproblemen suchen Sie nach einer Tatsache, die für nichtig erklärt werden kann (dh, etwas, das Sie ablehnen können).

Hypothesentestbeispiele # 1: Basisbeispiel

Ein Forscher ist der Meinung, dass Patienten mit Knieoperationen zweimal pro Woche (statt dreimal) zur Physiotherapie gehen, Ihre Erholungsphase wird länger sein. Die durchschnittliche Erholungszeit für Patienten mit Knieoperationen beträgt 8,2 Wochen.

Die Hypothese in dieser Frage ist, dass der Forscher glaubt, dass die durchschnittliche Erholungszeit mehr als 8,2 Wochen beträgt. Es kann mathematisch geschrieben werden als:
H1: μ > 8.,2

Als nächstes müssen Sie die Nullhypothese angeben (Siehe: Wie man die Nullhypothese angibt). Das wird passieren, wenn der Forscher falsch liegt. Wenn der Forscher im obigen Beispiel falsch liegt, beträgt die Erholungszeit weniger als oder gleich 8,2 Wochen. In der Mathematik, das ist:
H0 μ ≤ 8.2

Ablehnung der Nullhypothese

Vor etwa zehn Jahren glaubten wir, dass es 9 Planeten im Sonnensystem gab. Pluto wurde 2006 als Planet degradiert. Die Nullhypothese von “ Pluto ist ein Planet „wurde ersetzt durch“ Pluto ist kein Planet.,“Natürlich ist es nicht immer so einfach, die Nullhypothese abzulehnen—der schwierige Teil besteht normalerweise darin, herauszufinden, was Ihre Nullhypothese überhaupt ist.

Beispiele für Hypothesentests (Ein Sample Z-Test)

Der One Sample z-Test wird nicht sehr häufig verwendet (da wir selten die tatsächliche Standardabweichung der Population kennen). Es ist jedoch eine gute Idee zu verstehen, wie es funktioniert, da es einer der einfachsten Tests ist, die Sie in Hypothesentests durchführen können., Im Englischunterricht musst du die Grundlagen (wie Grammatik und Rechtschreibung) lernen, bevor du eine Geschichte schreiben kannst; Stellen Sie sich einen Beispiel-z-Test als Grundlage für das Verständnis komplexerer Hypothesentests vor. Diese Seite enthält zwei Hypothesentestbeispiele für eine Probe z-Tests.

Eine Beispielhypothese Testbeispiele: #2

Ein Schulleiter an einer bestimmten Schule behauptet, dass die Schüler in seiner Schule überdurchschnittliche Intelligenz sind. Eine Zufallsstichprobe von dreißig Studenten IQ-Scores haben eine mittlere Punktzahl von 112., Gibt es genügend Beweise, um die Behauptung des Auftraggebers zu stützen? Der mittlere Populations-IQ beträgt 100 mit einer Standardabweichung von 15.

Schritt 1: Geben Sie die Nullhypothese an. Die akzeptierte Tatsache ist, dass der Populationsmittelwert 100 ist, also: H0: μ=100.

Schritt 2: Geben Sie die alternative Hypothese an. Die Behauptung ist, dass die Schüler überdurchschnittliche IQ-Werte haben, also:
H1: μ > 100.
Die Tatsache, dass wir für Partituren suchen „größer als“ ein bestimmter Punkt bedeutet, dass dies ein One-Tailed-Test.

Schritt 3: Zeichnen Sie ein Bild, um das Problem zu visualisieren.,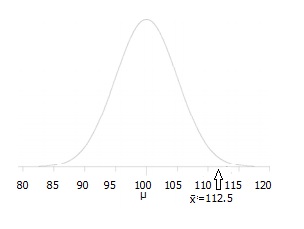

Schritt 4: Zustand der alpha-Ebene. Wenn Sie kein Alpha-Level erhalten, verwenden Sie 5% (0,05).

Schritt 5: Finden Sie die Ablehnung region (von der alpha-Ebene oben) aus der z-Tabelle. Ein Bereich von .05 entspricht einem z-score von 1.645.

Schritt 6: Finden Sie die Teststatistik mit dieser Formel: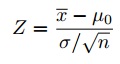
Für diesen Datensatz: z= (112.5 – 100) / (15/√30) = 4.56.

Schritt 6: Wenn Schritt 6 größer als Schritt 5 ist, lehnen Sie die Nullhypothese ab., Wenn es weniger als Schritt 5 ist, können Sie die Nullhypothese nicht ablehnen. In diesem Fall ist es größer (4.56 > 1.645), sodass Sie die null ablehnen können.

Ein Beispiel Hypothese zu Testen Beispiele: #3

Der Blutzuckerspiegel bei adipösen Patienten hat einen Mittelwert von 100 mit einer Standardabweichung von 15. Ein Forscher glaubt, dass sich eine Diät mit hohem Gehalt an roher Maisstärke positiv oder negativ auf den Blutzuckerspiegel auswirkt., Eine Stichprobe von 30 Patienten, die die rohe Maisstärke-Diät ausprobiert haben, hat einen mittleren Glukosespiegel von 140. Testen Sie die Hypothese, dass die rohe Maisstärke eine Wirkung hatte.

*Dieser Vorgang wird wesentlich erleichtert, wenn Sie mit einem TI-83 oder Excel den Z-Score (den „kritischen Wert“) berechnen.,
Siehe:

• Kritischer Z-Wert TI 83
• Z-Score in Excel

Beispiele für Hypothesentests: Mittelwert (Mit TI 83)

Sie können den TI 83-Rechner für Hypothesentests verwenden,aber der Rechner wird die Null-und Alternativhypothesen nicht herausfinden.

Beispielproblem: Eine Stichprobe von 200 Personen hat ein Durchschnittsalter von 21 Jahren mit einer Bevölkerungsstandardabweichung (σ) von 5. Testen Sie die Hypothese, dass der Populationsmittelwert 18,9 bei α = 0,05 beträgt.

Schritt 1: Geben Sie die Nullhypothese an., In diesem Fall ist die Nullhypothese, dass der Populationsmittelwert 18,9 ist, also schreiben wir:
H0: μ = 18,9

Schritt 2: Geben Sie die alternative Hypothese an. Wir möchten wissen, ob sich unsere Stichprobe mit einem Mittelwert von 21 anstelle von 18.9 wirklich von der Population unterscheidet, daher unsere alternative Hypothese:
H1: μ ≠ 18.9

Schritt 3: Drücken Sie Stat und drücken Sie dann zweimal den rechten Pfeil, um TESTS auszuwählen.

Schritt 4: Drücken Sie 1 zu wählen 1: Z-Test…. EINGABETASTE.

Schritt 5: Verwenden Sie den rechten Pfeil, um Statistiken auszuwählen.

Schritt 6: Geben Sie nun die Daten aus dem problem:
μ0: 18.,9
σ: 5
x: 21
n: 200
μ: ≠μ0

Schritt 7: Pfeil nach unten, um zu Berechnen, und drücken Sie die EINGABETASTE. Der Rechner zeigt den p-Wert:
p = 2.87 × 10-9

Dieser ist kleiner als unser alpha-Wert von .05. Das heißt, wir sollten die Nullhypothese ablehnen.

Bayesian Hypothesis Testing: Was ist das?

Bayesian hypothesis testing hilft, die Frage zu beantworten: Können die Ergebnisse eines Tests oder einer Umfrage wiederholt werden?
Warum kümmern wir uns, wenn ein Test wiederholt werden kann?, Nehmen wir an, zwanzig Menschen im selben Dorf erkrankten an Leukämie. Eine Gruppe von Forschern findet, dass Handy-Türme schuld sind. Eine zweite Studie ergab jedoch, dass Handy-Türme nichts mit dem Krebscluster im Dorf zu tun hatten. Tatsächlich stellten sie fest, dass die Krebsarten völlig zufällig waren. Wenn das unmöglich klingt, kann es tatsächlich passieren! Cluster von Krebs können einfach zufällig passieren. Es könnte viele Gründe geben, warum die erste Studie fehlerhaft war., Einer der Hauptgründe könnte sein, dass sie einfach nicht berücksichtigt haben, dass manchmal Dinge zufällig passieren und wir einfach nicht wissen warum.

P-Werte.

Es ist eine gute Wissenschaft, Leute wissen zu lassen, wenn Ihr die Ergebnisse der Studie sind solide, oder wenn Sie könnte haben passiert durch Zufall. Die übliche Methode besteht darin, Ihre Ergebnisse mit einem p-Wert zu testen. Ein p-Wert ist eine Zahl, die Sie durch Ausführen eines Hypothesentests für Ihre Daten erhalten. Ein P-Wert von 0,05 (5%) oder weniger reicht normalerweise aus, um zu behaupten, dass Ihre Ergebnisse wiederholbar sind., Es gibt jedoch eine andere Möglichkeit, die Gültigkeit Ihrer Ergebnisse zu testen: Bayesian Hypothesis testing. Diese Art von Tests gibt Ihnen eine andere Möglichkeit, die Stärke Ihrer Ergebnisse zu testen.

Bayes-Hypothese zu Testen.

Traditionelle Tests (der Typ, auf den Sie wahrscheinlich in elementaren Statistiken oder AP-Statistiken gestoßen sind) werden als Nicht-bayesisch bezeichnet. Es ist, wie oft ein Ergebnis über wiederholte Läufe des Experiments passiert. Es ist eine objektive Sicht darauf, ob ein Experiment wiederholbar ist.
Bayesian hypothesis testing ist eine subjektive Sicht auf die gleiche Sache., Es berücksichtigt, wie viel Vertrauen Sie in Ihre Ergebnisse haben. Mit anderen Worten, würden Sie Geld auf das Ergebnis Ihres Experiments setzen?

Unterschiede Zwischen der klassischen und der Bayes ‚ schen Hypothese zu Testen.

Traditionelle Tests (Nicht Bayesian) erfordern, dass Sie die Probenahme immer wieder wiederholen, während Bayesian-Tests dies nicht tun. Der Hauptunterschied zwischen den beiden besteht im ersten Testschritt: Angabe eines Wahrscheinlichkeitsmodells. In Bayesian Testing fügen Sie diesem Schritt Vorkenntnisse hinzu., Es erfordert auch die Verwendung einer hinteren Wahrscheinlichkeit, die die bedingte Wahrscheinlichkeit ist, die einem zufälligen Ereignis gegeben wird, nachdem alle Beweise berücksichtigt wurden.

Argumente für Bayes-Tests.

Viele Forscher denken, dass es eine bessere Alternative zu herkömmlichen Tests ist, weil es:

1. Vorkenntnisse über die Daten enthält.
2. berücksichtigt persönliche überzeugungen über die Ergebnisse.

Argumente gegen.

1. Das Einbeziehen von Vordaten oder Kenntnissen ist nicht zu rechtfertigen.
2. Im Vergleich zu nicht-bayesschen Tests ist es schwierig zu berechnen.,

Zurück nach oben

Artikel zum Testen von Hypothesen

Grundlagen:

1. Was ist Ad-hoc-Tests?
2. Zusammengesetzter Hypothesentest
3. Was ist eine Abstoßungsregion?
4. Was ist ein Test mit zwei Schwänzen?
5. So entscheiden Sie, ob ein Hypothesentest ein One-Tailed-Test oder ein Two-Tailed-Test ist.
6. So entscheiden Sie, ob eine Hypothese ein Test mit Linksschwanz oder ein Test mit Rechtsschwanz ist.
7. So geben Sie die Nullhypothese in der Statistik an.
8. So finden Sie einen kritischen Wert.
9. Wie man eine Nullhypothese unterstützt oder ablehnt.,

Spezifische Tests:

1. ANOVA.
2. Brunner-Munzel-Test (Generalized Wilcoxon-Test)
3. Chi-Quadrat-Test für Normalität
4. Cochran-Mantel-Haenszel-Test
5. F-Test
6. Granger-Kausalität-Test.
7. Hotellerie T-Squared
8. KPSS-Test.
9. Was ist ein Likelihood-Ratio-Test?
10. Log-rank-test.
11. MANCOVA
12. Sequentieller Wahrscheinlichkeitstest
13. So führen Sie einen Vorzeichentest aus.
14. T-Tests: one sample.
15. T-Test: Zwei probe.
16. Welchs ANOVA.
17. Welchs Test auf ungleiche Varianzen.,
18. Z-Test: ein Beispiel.
19. Z Test: Zwei Anteil
20. Wald Test.

1. Was ist eine Annahme-Region?
2. Wie berechnet man den Satz von Chebyshev?
3. entscheidungsregel.
4. Freiheitsgrade.
5. Richtungstest
6. Falsche Erkennungsrate
7. Wie berechnet man den geringsten signifikanten Unterschied?
8. Ebenen in der Statistik.
9. So berechnen Sie die Fehlerquote.
10. Mittlere Differenz (Unterschied in den Mitteln)
11. Das mehrfache Testproblem.
12. Was ist das Neyman-Pearson-Lemma?
13. Eine Probe Median-Test.,
14. REGWF
15. So finden Sie eine Beispielgröße (allgemeine Anweisungen).
16. Sig 2 (Tailed) Bedeutung in results
17. Was ist eine standardisierte Teststatistik?
18. So finden Sie Standardfehler
19. Standardisierte Werte: Beispiel.
20. Wie berechnet man einen T-Score?
21. T-Score Vs. ein Z-Score.
22. Testen eines einzelnen Mittels.
23. Ungleiche Stichprobengrößen.
24. Einheitlich Leistungsstärkste Tests.
25. Wie berechnet man einen Z-Score?

——————————————————————————

Benötigen Sie Hilfe bei Hausaufgaben oder Testfragen?, Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf diesem Gebiet. Ihre ersten 30 Minuten mit einem Chegg Tutor ist kostenlos!