Kumulative Frequenz
Archivierter Inhalt
Als archiviert identifizierte Informationen werden zu Referenz -, Forschungs-oder Aufzeichnungszwecken bereitgestellt. Es unterliegt nicht den Webstandards der Regierung von Kanada und wurde seit seiner Archivierung nicht geändert oder aktualisiert. Bitte kontaktieren Sie uns, um ein anderes als das verfügbare Format anzufordern.,
- Beispiel 1-Diskrete Variablen
- Beispiel 2-Kontinuierliche Variablen
- Andere kumulative Frequenzberechnungen
Die kumulative Frequenz wird verwendet, um die Anzahl der Beobachtungen zu bestimmen, die über (oder unter) einem bestimmten Wert in einem Datensatz liegen. Die kumulative Frequenz wird anhand einer Frequenzverteilungstabelle berechnet, die aus Stamm-und Blattdiagrammen oder direkt aus den Daten erstellt werden kann.
Die kumulative Frequenz wird berechnet, indem jede Frequenz aus einer Frequenzverteilungstabelle zur Summe ihrer Vorgänger addiert wird., Der letzte Wert ist immer gleich der Summe für alle Beobachtungen, da alle Frequenzen bereits zur vorherigen Summe hinzugefügt wurden.
Diskrete oder kontinuierliche Variablen
Variablen in jeder Berechnung können durch den ihnen zugewiesenen Wert charakterisiert werden. Eine diskrete Variable besteht aus separaten, unteilbaren Kategorien. Zwischen einer Variablen und ihrem Nachbarn können keine Werte existieren. Wenn Sie beispielsweise eine von Tag zu Tag registrierte Klassenbesuch beobachten, können Sie feststellen, dass die Klasse 29 Schüler an einem Tag und 30 Schüler an einem anderen Tag hat., Es ist jedoch unmöglich, dass die Teilnehmerzahl zwischen 29 und 30 liegt. (Es gibt einfach keinen Raum, Werte zwischen diesen beiden Werten zu beobachten, da es keine Möglichkeit gibt, 29einhalb Schüler zu haben.)
Nicht alle Variablen werden als diskret charakterisiert. Einige Variablen (wie Zeit, Größe und Gewicht) sind nicht auf einen festen Satz unteilbarer Kategorien beschränkt. Diese Variablen werden als kontinuierliche Variablen bezeichnet und sind in eine unendliche Anzahl möglicher Werte teilbar. Beispielsweise kann die Zeit in Bruchteilen von Stunden, Minuten, Sekunden und Millisekunden gemessen werden., Anstatt ein Rennen in 11 oder 12 Minuten zu beenden, können ein Jockey und sein Pferd die Ziellinie in 11 Minuten und 43 Sekunden überqueren.
Es ist wichtig, den Unterschied zwischen den beiden Variablentypen zu kennen, um ihre kumulative Häufigkeit richtig zu berechnen.
Beispiel 1-Diskrete Variablen
Die Gesamtzahl der Kletterer in Lake Louise, Alberta, wurde über einen Zeitraum von 30 Tagen aufgezeichnet. Die Ergebnisse sind wie folgt:
31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56, 4, 54, 39, 52, 35, 51, 63, 42.,e diskrete Variablen für:
- Richten Sie ein Stamm-und Blattdiagramm ein (siehe Abschnitt über Stamm-und Blattdiagramme) mit zusätzlichen Spalten mit der Bezeichnung Frequenz, oberer Wert und kumulative Häufigkeit
- Ermitteln Sie die Häufigkeit der Beobachtungen für jeden Stamm
- Ermitteln Sie den oberen Wert für jeden Stamm
- Berechnen Sie die kumulative Häufigkeit, indem Sie die Zahlen in der Spalte Frequenz
- Notieren Sie alle Ergebnisse im Diagramm
Antworten:
- Die Anzahl der Kletterer reicht von 4 bis 65. Um ein Stamm-und Blattdiagramm zu erstellen, werden die Daten am besten in Klassenintervallen von 10 gruppiert.
Jedes Intervall kann sich in der Stammsäule befinden. Die Zahlen in dieser Spalte stellen die erste Zahl innerhalb des Klassenintervalls dar. (Beispielsweise stellt Stamm 0 das Intervall 0-9, Stamm 1 das Intervall 10-19 usw. dar.)
Die Blattspalte listet die Anzahl der Beobachtungen auf, die innerhalb jedes Klassenintervalls liegen., Zum Beispiel werden in Stamm 2 (Intervall 20-29) die drei Beobachtungen 23, 24 und 26 als 3, 4 und 6 dargestellt.
Die Spalte Häufigkeit listet die Anzahl der Beobachtungen auf, die innerhalb eines Klassenintervalls gefunden wurden. Zum Beispiel wurden in Stamm 5 neun Blätter (oder Beobachtungen) gefunden; In Stamm 1 gibt es nur zwei.
Verwenden Sie die Spalte Frequenz, um die kumulative Frequenz zu berechnen.
- Fügen Sie zunächst die Nummer aus der Spalte Frequenz zu ihrem Vorgänger hinzu. Zum Beispiel haben wir in Stamm 0 nur eine Beobachtung und keine Vorgänger. Die kumulative Frequenz ist eins.,
1 + 0 = 1 - In Stamm 1 gibt es jedoch zwei Beobachtungen. Addieren Sie diese beiden zur vorherigen kumulativen Frequenz (eins), und das Ergebnis ist drei.
1 + 2 = 3 - Im Stamm 2, es gibt drei Beobachtungen. Addieren Sie diese drei zur vorherigen kumulativen Frequenz (drei) und die Summe (sechs) ist die kumulative Frequenz für Stamm 2.
3 + 3 = 6 - Setzen Sie diese Berechnungen fort, bis Sie alle Zahlen in der Spalte Frequenz addiert haben.
- Notieren Sie die Ergebnisse in der Spalte Kumulative Frequenz.,
In der Spalte Oberer Wert ist die Beobachtung (Variable) mit dem höchsten Wert in jedem Klassenintervall aufgeführt. Beispielsweise repräsentieren in Stamm 1 die beiden Beobachtungen 8 und 9 die Variablen 18 und 19. Der obere Wert dieser beiden Variablen ist 19.
Tabelle 1.,>8 9 2 19 1 + 2 = 3 2 3 4 6 3 26 3 + 3 = 6 3 1 5 5 7 9 5 39 6 + 5 = 11 4 0 1 2 3 5 9 6 49 11 + 6 = 17 5 0 1 1 2 4 4 5 6 7 9 57 17 + 9 = 26 6 0 2 3 5 4 65 26 + 4 = 30 - Fügen Sie zunächst die Nummer aus der Spalte Frequenz zu ihrem Vorgänger hinzu. Zum Beispiel haben wir in Stamm 0 nur eine Beobachtung und keine Vorgänger. Die kumulative Frequenz ist eins.,
- Since these variables are discrete, use the upper values in plotting the graph., Zeichnen Sie die Punkte zu einer kontinuierlichen Kurve, die als Ogive bezeichnet wird.
Beschriften Sie das Diagramm immer mit der kumulativen Häufigkeit-entsprechend der Anzahl der Beobachtungen-auf der vertikalen Achse.,vergleichen Sie die horizontale Achse mit der anderen Variablen (in diesem Fall zählt der gesamte Kletterer) wie unten gezeigt:
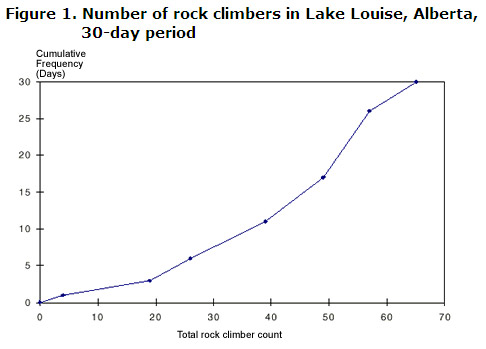
Die folgenden Informationen können entweder aus der Grafik oder Tabelle gewonnen werden:
- An 11 der 30 Tage kletterten 39 Personen oder weniger auf die Felsen um Lake Louise
- an 13 der 30 Tage kletterten 50 oder mehr Personen auf die Felsen um Lake Louise
Wenn eine kontinuierliche Variable verwendet wird, erfordern sowohl die Berechnung der kumulativen Frequenz als auch das Zeichnen des Diagramms einen etwas anderen Ansatz als bei einer diskreten Variablen.,
Beispiel 2 – Kontinuierliche Variablen
Für 25 Tage, die Schneehöhe am Whistler Mountain, B. C. gemessen wurde (die zentimetergenaue) und notiert, wie folgt:
242, 228, 217, 209, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257.,
- Verwenden Sie die obigen kontinuierlichen Variablen, um:
- Richten Sie eine Frequenzverteilungstabelle ein
- Suchen Sie die Frequenz für jedes Klassenintervall
- Suchen Sie den Endpunkt für jedes Klassenintervall
- Berechnen Sie die kumulative Frequenz, indem Sie die Zahlen in der Frequenzspalte
- Notieren Sie alle Ergebnisse in der Tabelle
- Verwenden Sie die Informationen aus der Frequenzverteilungstabelle, um ein kumulatives Frequenzdiagramm zu zeichnen.
Antworten:
- Die Schneetiefenmessungen reichen von 209 cm bis 266 cm., Um die Frequenzverteilungstabelle zu erstellen, werden die Daten am besten in Klassenintervallen von jeweils 10 cm gruppiert.
In der Schneetiefenspalte ist jedes 10-cm-Klassenintervall von 200 cm bis 270 cm aufgeführt.
Die Spalte Häufigkeit zeichnet die Anzahl der Beobachtungen auf, die in ein bestimmtes Intervall fallen. Diese Spalte stellt die Beobachtungen in der Spalte Tally nur in numerischer Form dar.,
Die Endpunktspalte funktioniert ähnlich wie die obere Wertespalte von Übung 1, mit der Ausnahme, dass der Endpunkt die höchste Zahl im Intervall ist, unabhängig vom tatsächlichen Wert jeder Beobachtung. Im Klassenintervall von 210-220 beträgt der tatsächliche Wert der beiden Beobachtungen beispielsweise 217 und 219. Anstelle von 219 wird jedoch der Endpunkt 220 verwendet.
Die Spalte Kumulative Frequenz listet die Summe jeder Frequenz auf, die zu ihrem Vorgänger hinzugefügt wurde.
Tabelle 2. Schneehöhe gemessen am Whistler Mountain, B. C.,e2cd5a9″> 5 240 11 240 to < 250 
7 250 18 250 to < 260 
5 260 23 260 to < 270 
2 270 25 - Because the variable is continuous, the endpoints of each class interval are used in plotting the graph., Die gezeichneten Punkte sind zu einem Ogiv verbunden.
Denken Sie daran, dass die kumulative Häufigkeit (Anzahl der Beobachtungen) auf der vertikalen y-Achse und jede andere Variable (Schneetiefe) auf der horizontalen x-Achse wie in Abbildung 2 dargestellt gekennzeichnet ist.,

Die folgenden Informationen können entweder aus einer Grafik oder einer Tabelle gewonnen werden:
- Keiner der 25 Tage hatte eine Schneehöhe von weniger als 200 cm
- Einer der 25 Tage Schnee hatte eine Tiefe von weniger als 210 cm
- zwei der 25 Tage Schnee hatten eine Tiefe von 260 cm oder mehr
Andere kumulative Häufigkeit berechnungen
Eine weitere Berechnung, die mit einer Frequenzverteilungstabelle erhalten werden kann, ist die relative Frequenzverteilung. Diese Methode ist definiert als der Prozentsatz der Beobachtungen, die in jedem Klassenintervall fallen., Die relative kumulative Häufigkeit kann ermittelt werden, indem die Häufigkeit jedes Intervalls durch die Gesamtzahl der Beobachtungen dividiert wird. (Weitere Informationen finden Sie unter Frequenzverteilung im Kapitel Organisieren von Daten.)
Zur Berechnung des kumulativen Prozentsatzes kann auch eine Frequenzverteilungstabelle verwendet werden. Diese Methode der Frequenzverteilung gibt uns den Prozentsatz der kumulativen Frequenz an, im Gegensatz zu dem Prozentsatz nur der Frequenz.