- Historischer Hintergrund
- Scheinbare Magnitude, m
- Absolute Magnitude, M
- Ermitteln der Entfernung zu Sternen-Entfernungsmodul
- Magnitude / Entfernungsberechnungen
- Benennung & Sterne identifizieren
Untersuchen Sie das unten gezeigte Sternfeldfoto. Es zeigt eine Region des Himmels um das Sternbild Crux, allgemein als südliches Kreuz bezeichnet. Bewegen Sie den Cursor über das Foto, um einige Sterne zu identifizieren.
Welcher Stern ist am hellsten?,

Wenn Sie Alpha (α) Centauri beantwortet haben, ist der Stern unten links auf dem Foto rechts. Wie Sie sehen, zeigt ein fotografisches Bild wie dieses viel mehr Sterne, als Sie mit bloßem Auge sehen können. Dennoch sind einige Stars prominenter als andere. Bei der Auswahl von α Centauri haben Sie einige Annahmen getroffen. Was waren Sie?
Ein Foto wie dieses zeigt helle Sterne als größere Scheiben als schwächere Sterne., Bedeutet dies, dass diese Sterne physisch größer sind als die schwächeren Sterne auf dem Foto? Denken Sie daran, im Abschnitt über Astrometrie haben wir gelernt, dass alle Sterne außer unserer Sonne so weit entfernt sind, dass sie effektiv Punktquellen sind. Warum erscheinen einige dann heller (für unsere Augen) oder größer (auf Fotos) als andere? Was ist eigentlich Helligkeit und wie können wir sie messen? Die Antworten auf diese Fragen bilden den Schwerpunkt dieses Abschnitts.,
Historischer Hintergrund

Das Konzept der Messung und des Vergleichs der Helligkeit von Sternen lässt sich auf den griechischen Astronomen und Mathematiker Hipparchus (190-120 v. Chr.) zurückführen. Als einer der größten Astronomen der Antike wird ihm die Erstellung eines Katalogs von 850 Sternen mit Positionen und vergleichenden Hellheiten zugeschrieben., In seinem System, Den hellsten Sternen wurde eine Größe von zugewiesen 1, die nächste hellste Größe 2 und so weiter zu den schwächsten Sternen, nur sichtbar für das bloße Auge, die Größe waren 6. Diese Sechs-Punkte-Skala kann als Ranking gedacht werden, erstklassige Sterne, die hellsten, waren erste Größenordnung und die niederfrequenten Sterne waren sechste Größenordnung.
Die Entdeckung schwacherer Sterne mit Teleskopen in den frühen 1600er Jahren erforderte eine Ausdehnung der Skala über die Größe 6 hinaus., Die Entwicklung von visuellen Photometern, Instrumenten zur Messung der Sternintensitäten, im neunzehnten Jahrhundert von John Herschel und anderen veranlasste die Astronomen, einen internationalen Standard einzuführen. Die Tatsache, dass Augen Intensitätsunterschiede eher logarithmisch als linear erkennen, wurde in den 1830er Jahren entdeckt. 1856 schlug Norman Pogson vor, dass ein Stern der Magnitude 1 100 × heller als ein Stern der Magnitude 6 sei. Ein Unterschied von einer Größe war daher gleich 5√100 = 2.512 mal in der Helligkeit.,
Scheinbare Größe, m
Die scheinbare Größe, m, eines Sterns ist die Größe, die er hat, wie er von einem Beobachter auf der Erde gesehen wird.
Ein sehr helles Objekt wie die Sonne oder der Mond kann eine negative scheinbare Größe haben. Obwohl Hipparchus ursprünglich den hellsten Sternen eine Größe von 1 zugewiesen hatte, zeigt ein sorgfältigerer Vergleich, dass der hellste Stern am Nachthimmel, Sirius oder α Canis Majoris (CMa), tatsächlich eine scheinbare Größe von m = -1.44 hat. Mit der Neukalibrierung der ursprünglichen Werte von Hipparchus hat der helle Stern Vega nun eine scheinbare Größe von 0,0.,
Nach der teleskopischen Entdeckung schwacher Sterne in den frühen 1600er Jahren musste die Magnitudenskala auch auf Objekte ausgedehnt werden, die schwächer als die Magnitude 6 waren. Die folgende Tabelle zeigt den Bereich der scheinbaren Größen für Himmelsobjekte.
| Objekt | Objekt |
|---|---|
| Sonne |
-26.5
|
| Vollmond |
-12.5
|
| Venus |
-4.,3
|
| Mars or Jupiter |
-2
|
| Sirius (α CMa) |
-1.44
|
| Vega (α Lyr) |
0.0
|
| Alnair (α Gru) |
1.73
|
| Naked-eye limit |
6.5
|
| Binocular limit |
10
|
| Proxima Cen |
11.,09
|
| Visual limit through 20 cm telescope |
14
|
| QSO at redshift z = 2 |
≈ 20
|
| Cepheid in galaxy M100 observed with HST |
26
|
| Galaxy at z = 6 observed with Gemini 8.1 m telescope |
28
|
| Limit for James Webb Space Telescope |
≥ 30
|
If a star of magnitude 1 is 2.,512 × heller als ein Stern der Magnitude 2 und 100 &mal heller als ein Stern der sechsten Magnitude wie viel heller ist es als ein Stern der Magnitude 3? Sie müssen hier vorsichtig sein. Es ist nicht einfach 2 × 2.512 anders. Sie müssen sich daran erinnern, dass eine Differenz von einer Größe gleich 5√100 = 2,512 ist. Ein Unterschied von 2 Größen ist daher = 2,5122 = 6,31 × Helligkeitsunterschied.
Zwei Objekte unterschiedlicher Größe variieren daher in der Helligkeit um 2,512 bis zur Stärke der Größendifferenz., Wenn wir dies als Gleichung schreiben, wird das Verhältnis von Helligkeit oder Intensität IA/IB zwischen zwei Objekten A und B mit den Größen mA und mB durch die folgende Gleichung gegeben:
Schauen wir uns ein Beispiel an.
Beispiel 1: Vergleich zweier Sterne.
Wie viel heller ist Alnair, scheinbare Größe von + 1,73 als Proxima Cen mit einer Größe von 11,09?
Mit Gleichung 4.1 haben wir:
also ersetzt durch:
Beispiel 2: Wie viel heller ist die Sonne als der Vollmond?
Dafür erinnern wir uns aus der obigen Tabelle, dass die Sonne eine scheinbare Größe von -26,5 und der Vollmond, – 12,5 hat.
So mit Gleichung 4.1 erhalten wir:
das in uns gibt:
Es ist wichtig, sich daran zu erinnern, dass Größe einfach eine Zahl ist, sie hat keine Einheiten. Das Symbol für die scheinbare Größe ist ein Kleinbuchstabe m; Sie müssen dies bei jedem Problem klarstellen.
Absolute Magnitude, M
Was sagt uns die Tatsache, dass Sirius eine scheinbare Magnitude von -1.44 und Betelgeuse eine scheinbare Magnitude von 0.45 hat, über diese beiden Sterne? Eine andere Art, darüber nachzudenken, ist zu fragen, warum Sirius der hellste Stern am Nachthimmel ist., Ein Stern kann aus zwei Hauptgründen hell erscheinen:
- Er kann eigenleuchtend sein, dh er kann ein starker Emitter elektromagnetischer Strahlung sein, oder
- Er kann uns sehr nahe sein oder beides.
Die scheinbare Größe eines Sterns hängt daher teilweise von seiner Entfernung von uns ab. Tatsächlich erscheint Sirius heller als Betelgeuse, gerade weil Sirius uns sehr nahe steht, nur 2.6 PC entfernt, während Betelgeuse etwa 160 PC entfernt ist., Die Erkenntnis, dass Sterne nicht alle die gleiche Leuchtkraft haben, bedeutete, dass die scheinbare Größe allein nicht ausreichte, um Sterne zu vergleichen. Ein neues System, mit dem Astronomen Sterne direkt vergleichen können, wurde entwickelt. Dieses System wird als absolute Magnitude bezeichnet, M.
Die absolute Magnitude M eines Sterns ist die Magnitude, die ein Stern in einer Entfernung von 10 Parsec von uns hätte. Eine Entfernung von 10 pc ist rein willkürlich, aber jetzt international von Astronomen vereinbart., Die skala für absolute größe ist die gleiche wie die für scheinbare größe, das ist eine differenz von 1 größe = 2,512 mal unterschied in helligkeit. Diese logarithmische Skala ist auch offen und einheitenlos. Je niedriger oder negativer der Wert von M ist, desto heller ist der Stern. Absolute Größe ist eine bequeme Möglichkeit, die Leuchtkraft eines Sterns auszudrücken. Sobald die absolute Größe eines Sterns bekannt ist, können Sie ihn auch mit anderen Sternen vergleichen. Betelgeuse, M = -5.6 ist intrinsisch leuchtender als Sirius mit einem M = 1.41.
Unsere Sonne hat eine absolute visuelle Größe von 4,8.,
Ermitteln der Entfernung zu Sternen-Entfernungsmodul
Wie Sie sich vielleicht aus dem Abschnitt über Astrometrie erinnern, sind die meisten Sterne zu weit entfernt, um ihre Parallaxe direkt messen zu lassen. Wenn Sie jedoch sowohl die scheinbare als auch die absolute Größe eines Sterns kennen, können Sie dessen Entfernung bestimmen. Schauen wir uns noch einmal Sirius und Betelgeuse sowie einen weiteren Stern namens GJ 75 an.
Wie weit ist GJ 75? Es ist ein ungewöhnlicher Stern, da seine scheinbaren und absoluten Größen gleich sind. Warum? Der Grund dafür ist, dass es tatsächlich 10 Parsecs von uns entfernt ist, so dass per Definition seine beiden Größen gleich sein müssen.,
Was ist mit Sirius? Seine scheinbare Größe ist niedriger (daher heller) als seine absolute Größe. Dies bedeutet, dass es näher als 10 Parsecs zu uns ist. Die scheinbare Größe von Betelgeuse ist höher (daher dimmer) als ihre absolute Größe, so dass sie am Nachthimmel noch heller erscheint, wenn sie nur 10 Parsec entfernt wäre.
Astronomen verwenden den Unterschied zwischen scheinbarer und absoluter Größe, den Abstandsmodul, um die Entfernung zu einem Stern zu de terminieren.
- Distanzmodul = m-M.
- Distanzmodul ist negativ für Sterne näher als 10 parsecs.,
- Distanzmodul ist positiv für Sterne weiter weg als 10 parsecs.
- Die Größe des Abstandsmoduls bestimmt den tatsächlichen Wert der Entfernung, so dass ein Stern des Abstandsmoduls 1,5 näher als einer mit einem Abstandsmodul von 8,7 ist.
Magnitude / Distanzberechnungen
Mit dem Distanzmodul kann der Abstand zu einem Stern anhand der Gleichung bestimmt werden:
wobei d in parsecs enthalten ist. Beachten Sie, dass, wenn d = 10 pc dann m und M gleich sind. (Eine formale Ableitung dieser Gleichung ist auf der nächsten Seite zur Leuchtkraft angegeben)., NSW HSC Syllabus Formel Blatt stellt die Gleichung als:
aber das ist einfach nur eine überarbeitung von Gleichung 4.2. Sie sollten diese Gleichung bei zwei der drei Variablen bequem lösen können. Lassen Sie uns wissen, wie Sie einige Beispiele lösen können.
Beispiel 3: Gegeben m und d, finden müssen M.
β Crucis (oder Mimose) hat eine scheinbare Größe von 1,25 und ist 108 parsecs entfernt. Was ist seine absolute Größe?
Mit Gleichung 4.3 haben wir:
β Crucis hat also eine absolute Größe von -3.92
Beachten Sie, dass diese Berechnung voll funktioniert hat, sodass jeder Schritt explizit ist. (Denken Sie daran, bei der Lösung von Magnitudengleichungen log bezieht sich auf Logarithmen auf Basis 10 und nicht natürliche Logarithmen oder ln.)
Beispiel 4: Gegeben m und M, finden d.
Betelgeuse hat eine scheinbare Größe von 0,45 und eine absolute Größe von -5,14. Wie weit ist es entfernt?
Dieses Problem erfordert, dass wir Gleichung 4.2 neu schreiben, um uns d als das Unbekannte zu geben., Dies ist unten dargestellt:
jetzt ersetzen in:
Betelgeuse ist also ca.
Dieses Beispiel zeigt erneut die vollständige Arbeit, während Sie in Wirklichkeit möglicherweise nicht jeden Schritt anzeigen., Es ist jedoch wichtig, dass Sie Ihre Arbeit für solche Probleme klar festlegen, damit Sie Ihre algebraische Manipulation und Ihre Substitutionen überprüfen können. Die Arbeit mit Protokollen und Indizes kann schwierig sein, damit Sie wissen, wie diese auf Ihrem Rechner zu tun.
Beispiel 5: Gegeben M und d, finden m.
In der Praxis ist diese Art von Problem für tatsächliche Objekte weniger realistisch, da wir normalerweise ihre scheinbaren Größen direkt messen können, es kann jedoch sein, dass wir berechnen möchten, welche scheinbare Größe eine Klasse oder ein Objekttyp die anderen Parameter angegeben hat. Wieder, beginnend mit Gleichung 4.,3 lassen Sie uns bestimmen, wie hell ein Überriese wie Deneb mit einer absoluten Größe von -8,73 erscheinen würde, wenn er 230 Parsec entfernt wäre.
also Ersetzen in:
Deneb hätte also eine scheinbare Größe von -1.89. Dies würde es in unserem Nachthimmel heller machen als Sirius (m = -1.44)., In Wirklichkeit ist Deneb etwa 990 pc entfernt, obwohl dieser Wert eine große Unsicherheit aufweist.
Beispiel 6: Was ist, wenn d nicht gegeben ist, aber Parallaxe, p gegeben ist?
Das ist eigentlich sehr geradlinig. Aus dem Abschnitt über Astrometrie geht hervor, dass eine direkte Beziehung zwischen Entfernung und Parallaxe besteht.
Sie müssen dies also einfach in Gleichung 4.2 oder 4.3 einfügen.
Namensgebung & Erkennen Stars
Lassen Sie uns wissen, überdenken, das Foto von Crux und die Zeiger aus, die oben auf dieser Seite., Das Foto unten zeigt dieselbe Region mit den markanten Sternen. Sie haben auch ihre scheinbaren Größen gezeigt. Crux ist eine Konstellation, eine von 88 Regionen, in die die Himmelssphäre zerlegt und international von Astronomen vereinbart wurde. Crux ist eigentlich das kleinste der Konstellationen und ist am südlichen Himmel leicht zu erkennen. Die prominenten Sterne in der Nähe, die üblicherweise als Zeiger bezeichnet werden, sind tatsächlich Teil einer großen Konstellation namens Centaurus.

Jetzt können Sie feststellen, dass die Sterne mit Buchstaben aus dem griechischen Alphabet benannt werden; α, β, γ δ und ε (alpha, beta, Gamma, Delta, Epsilon sind die ersten fünf), gefolgt von der Standard-Abkürzung mit drei Buchstaben für jede Konstellation (Cru für Crucis oder Crux und Cen für Centaurus). Wenn Sie sich die scheinbaren Größen der fünf genannten Sterne in Crux genau ansehen, werden Sie feststellen, dass der hellste Stern mit α, der nächste β usw. gekennzeichnet ist., Dieses System wird nach Johann Bayer, der es 1603 einführte, Bayer-System genannt. Dem hellsten Stern in einer Konstellation wird der Buchstabe α, der nächste β usw. zugewiesen. Eine Ausnahme von dieser Regel ist &alpha Orionis oder Beteigeuze. Es ist in der Tat schwächer als β Ori, Rigel durch eine kleine Menge. Dies ist ein interessanter historischer Fall, der durch die Erkenntnis gelöst wurde, dass Betelgeuse seit seiner Benennung nach dem Bayer-System leicht an Helligkeit eingebüßt hat.,
Ein Punkt, an den man sich bei Sternbildern erinnern sollte, ist, dass die Sterne innerhalb einer Konstellation im Gegensatz zu Sternen in Clustern normalerweise nicht physisch miteinander verbunden sind. Die Tatsache, dass nahe beieinander erscheinen, ist ein reiner Ausrichtungseffekt entlang der Sichtlinie. Tatsächlich sind die Sterne in der obigen Region weit voneinander entfernt, wie im nächsten Bild gezeigt.
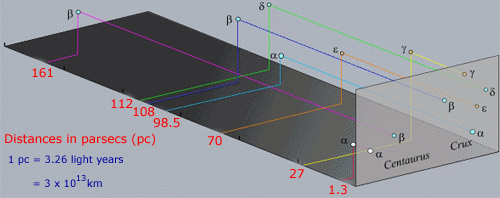
Einige der hellen Sterne wie α Cen haben auch ihren eigenen spezifischen Namen. Sirius (α Sco) ist ein solches Beispiel, während α Cen auch Rigel Kentaurus genannt wird. Viele Sternnamen sind arabischen Ursprungs aus der Zeit, als griechische Aufzeichnungen von islamischen Astronomen aufbewahrt und entwickelt wurden. Das Problem mit dem neuen System der Benennung von Sternen ist, dass es nur 24 Buchstaben im griechischen Alphabet gibt, aber es gibt viel mehr Sterne als in jeder Konstellation.
Die meisten Sterne haben tatsächlich keinen bestimmten Namen oder eine bestimmte Klassifizierung., Heutzutage haben Astronomen riesige Kataloge von Sternen zusammengestellt, einige mit über 10 Millionen Objekten, so dass die meisten Sterne nur eine Katalognummer haben. Sterne können viel mehr als einen Identifikationsnamen oder eine Katalognummer haben, abhängig von der Anzahl der Kataloge, in denen sie sich befinden. Der variable Stern δ Cep wird beispielsweise auch als HIP 110991, SAO 34508 oder einer von mehr als 30 anderen Kennungen bezeichnet! Viele Kataloge verwenden Himmelskoordinaten wie den rechten Aufstieg und die Deklination, um Objekte zu identifizieren. Somit ist δ Cep als IRAS 22273+5809, CCDM J22292+5825A und AAVSO 2225+57 bekannt., Die leichten Schwankungen in RA und dec für die Kataloge entstehen durch die richtige Bewegung der Sterne und die Präzession des Referenzrahmens.