- Antecedentes históricos
- magnitud aparente, M
- magnitud absoluta, M
- encontrar la distancia a las estrellas – Módulo de distancia
- cálculos de magnitud/distancia
- Naming& identificar estrellas
estudie la fotografía de campo estelar que se muestra a continuación. Muestra una región del cielo alrededor de la constelación Crux, comúnmente llamada La Cruz Del Sur. Mueve el cursor por la foto para identificar algunas estrellas.
¿Qué estrella es más brillante?,

si respondiste Alfa (α) Centauri, La estrella en la parte inferior izquierda de la fotografía estás a la derecha. Como puedes ver, una imagen fotográfica como esta muestra muchas más estrellas de las que puedes ver a simple vista. Sin embargo, algunas estrellas son más prominentes que otras. Al elegir α Centauri hiciste algunas suposiciones. ¿Qué eran?
una fotografía como esta muestra estrellas brillantes como discos más grandes que estrellas más débiles., ¿Significa esto que estas estrellas son físicamente más grandes que las estrellas más débiles de la foto? Recuerde, en la sección Sobre astrometría aprendimos que todas las estrellas que no sean nuestro Sol están tan distantes que son efectivamente fuentes puntuales. ¿Por qué entonces algunos parecen más brillantes (a nuestros ojos) o más grandes (en fotografías) que otros? ¿Qué es, de hecho, el brillo y cómo podemos medirlo? Las respuestas a estas preguntas forman el foco de esta sección.,
antecedentes históricos

el concepto de medir y comparar el brillo de las estrellas se remonta al astrónomo y matemático griego Hiparco (190-120 AC). Uno de los más grandes astrónomos de la antigüedad, se le atribuye la producción de un catálogo de 850 estrellas con posiciones y brillos comparativos., En su sistema, a las estrellas más brillantes se les asignó una magnitud de 1, la siguiente magnitud más brillante 2 y así sucesivamente a las estrellas más débiles, solo visibles a simple vista, que eran de magnitud 6. Esta escala de seis puntos puede considerarse como una clasificación, Las estrellas de primera categoría, las más brillantes, eran de primera magnitud y las estrellas de baja intensidad tenues eran de sexta magnitud.
el descubrimiento de estrellas más débiles con telescopios a principios de 1600 requirió que la escala se extendiera más allá de la magnitud 6., El desarrollo de fotómetros visuales, instrumentos para medir intensidades estelares, en el siglo XIX por John Herschel y otros impulsó la necesidad de que los astrónomos adopten un estándar internacional. El hecho de que los ojos detecten diferencias en la intensidad logarítmicamente en lugar de linealmente fue descubierto en la década de 1830. en 1856 Norman Pogson propuso que una estrella de magnitud 1 era 100 × más brillante que una estrella de magnitud 6. Una diferencia de una magnitud era por lo tanto igual a 5√100 = 2.512 veces en brillo.,
Magnitud Aparente m
La magnitud aparente, m, de una estrella es la magnitud que tiene como visto por un observador en la Tierra.
un objeto muy brillante, como el sol o la Luna, puede tener una magnitud aparente negativa. A pesar de que Hipparchus originalmente asignó a las estrellas más brillantes una magnitud de 1, una comparación más cuidadosa muestra que la estrella más brillante en el cielo nocturno, sirio o α Canis Majoris (CMA) en realidad tiene una magnitud aparente de m = -1.44. Con la recalibración de los valores originales de Hipparchus, la estrella brillante Vega ahora se define como una magnitud aparente de 0.0.,
tras el descubrimiento telescópico de estrellas débiles a principios de 1600, la escala de magnitud también ha tenido que extenderse a objetos más débiles que la magnitud 6. La siguiente tabla muestra el rango de magnitudes aparentes de los objetos celestes.
| Objeto | Aparente Magnitud |
|---|---|
| Sol |
-26.5
|
| Luna Llena |
-12.5
|
| Venus |
-4.,3
|
| Mars or Jupiter |
-2
|
| Sirius (α CMa) |
-1.44
|
| Vega (α Lyr) |
0.0
|
| Alnair (α Gru) |
1.73
|
| Naked-eye limit |
6.5
|
| Binocular limit |
10
|
| Proxima Cen |
11.,09
|
| Visual limit through 20 cm telescope |
14
|
| QSO at redshift z = 2 |
≈ 20
|
| Cepheid in galaxy M100 observed with HST |
26
|
| Galaxy at z = 6 observed with Gemini 8.1 m telescope |
28
|
| Limit for James Webb Space Telescope |
≥ 30
|
If a star of magnitude 1 is 2.,512 × más brillante que una estrella de magnitud 2 y 100 & veces más brillante que una estrella de sexta magnitud ¿cuánto más brillante es que una estrella de magnitud 3? Tienes que tener cuidado aquí. No es simplemente 2 × 2.512 diferente. Es necesario recordar que una diferencia de una magnitud es igual a 5√100 = 2.512. Una diferencia de 2 magnitudes por lo tanto = 2.5122 = 6.31 × diferencia en brillo.
dos objetos de diferentes magnitudes por lo tanto varían en brillo por 2.512 elevado a la potencia de la diferencia de magnitud thee., Si escribimos esto como una ecuación, la relación de brillo o intensidad, IA/IB entre dos objetos, A y B, con magnitudes mA y mB está dada por la siguiente ecuación:
echemos un vistazo a un ejemplo.
Ejemplo 1: Comparación de dos estrellas.¿cuánto más brillante es Alnair, magnitud aparente de +1.73 que Proxima Cen con una magnitud de 11.09?
Utilizando la ecuación 4.1, tenemos:
por lo que, sustituyendo en:
Ejemplo 2: ¿cuánto más brillante es el sol que la luna llena?
Para esto recordamos de la tabla anterior que el Sol tiene una magnitud aparente de -26.5 y la luna llena, – 12.5.
Entonces, utilizando la ecuación 4.1, se obtiene:
sustituyendo en la que nos da:
es importante recordar que la magnitud es simplemente un número, no tiene ninguna unidad. El símbolo de magnitud aparente es una m minúscula; debe dejar esto claro en cualquier problema.
magnitud absoluta, M
¿Qué nos dice el hecho de que Sirio tenga una magnitud aparente de -1,44 y Betelgeuse una magnitud aparente de 0,45 sobre estas dos estrellas? Otra forma de pensar sobre esto es preguntar ¿por qué es sirio la estrella más brillante en el cielo nocturno?, Una estrella puede aparecer brillante por dos razones principales:
- Puede ser intrínsecamente luminosa, es decir, puede ser un potente emisor de radiación electromagnética, o
- Puede estar muy cerca de nosotros, o ambas.
la magnitud aparente de una estrella depende en parte de su distancia de Nosotros. De hecho, Sirius parece más brillante que Betelgeuse precisamente porque Sirius está muy cerca de nosotros, a solo 2.6 pc de distancia, mientras que Betelgeuse está a unos 160 PC de distancia., La comprensión de que las estrellas no tienen todas la misma luminosidad significaba que la magnitud aparente por sí sola no era suficiente para comparar estrellas. Se desarrolló un nuevo sistema que permitiría a los astrónomos comparar directamente las estrellas. Este sistema se llama la magnitud absoluta, M.
la magnitud absoluta, M, de una estrella es la magnitud que la estrella tendría si estuviera a una distancia de 10 pársecs de Nosotros. Una distancia de 10 pc es puramente arbitraria, pero ahora acordada internacionalmente por los astrónomos., La escala de magnitud absoluta es la misma que para la magnitud aparente, que es una diferencia de 1 magnitud = 2.512 veces la diferencia en el brillo. Esta escala logarítmica también es abierta y sin unidades. De nuevo, cuanto más bajo o más negativo es el valor de M, más brillante es la estrella. La magnitud absoluta es una forma conveniente de expresar la luminosidad de una estrella. Una vez que se conoce la magnitud absoluta de una estrella, también se puede comparar con otras estrellas. Betelgeuse, M = -5.6 es intrínsecamente más luminoso que Sirio con un M = 1.41.
nuestro Sol tiene una magnitud visual absoluta de 4.8.,
encontrar la distancia a las estrellas – Módulo de distancia
como puede recordar de la sección Sobre astrometría, la mayoría de las estrellas están demasiado distantes para que su paralaje se mida directamente. Sin embargo, si conoces las magnitudes aparentes y absolutas de una estrella, puedes determinar su distancia. Miremos de nuevo a Sirio y Betelgeuse más otra estrella llamada GJ 75.
¿A qué distancia está GJ 75? Es una estrella inusual en que sus magnitudes aparentes y absolutas son las mismas. ¿Por qué? La razón es que en realidad está a 10 pársecs lejos de nosotros, por lo que por definición sus dos magnitudes deben ser las mismas.,
¿Qué pasa con Sirius? Su magnitud aparente es menor (por lo tanto más brillante) que su magnitud absoluta. Esto significa que está más cerca de 10 pársecs a nosotros. La magnitud aparente de Betelgeuse es mayor (por lo tanto más tenue) que su magnitud absoluta, por lo que parecería aún más brillante en el cielo nocturno si estuviera a solo 10 pársecs de distancia.
Los astrónomos utilizan la diferencia entre la magnitud aparente y absoluta, el módulo de distancia, como una forma de definir la distancia a una estrella.
- Módulo de distancia = m-M.
- El módulo de distancia es negativo para las estrellas más cercanas a 10 pársecs.,
- El módulo de distancia es positivo para estrellas más alejadas de 10 pársecs.
- El tamaño del módulo de distancia determina el valor real de la distancia, de modo que una estrella de módulo de distancia 1.5 está más cerca que una con un módulo de distancia de 8.7.
cálculos de magnitud / distancia
El módulo de distancia se puede utilizar para determinar la distancia a una estrella utilizando la ecuación:
donde d está en parsecs. Tenga en cuenta que si d = 10 pc entonces m y M son lo mismo. (Una derivación formal de esta ecuación se da en la página siguiente sobre luminosidad)., La hoja de fórmulas NSW HSC Syllabus proporciona la ecuación como:
pero esto es simplemente una reelaboración de la ecuación 4.2. Usted debe estar cómodo en la solución de esta ecuación dada dos de las tres variables. Déjanos saber mira cómo puedes resolver algunos ejemplos.
Ejemplo 3: dados m y d, necesidad de encontrar M.
β Crucis (o Mimosa) tiene una magnitud aparente de 1.25 y está a 108 pársecs de distancia. ¿Cuál es su magnitud absoluta?
Usando la ecuación 4.3 tenemos:
así que β Crucis tiene una magnitud absoluta de -3.92
Nota Este cálculo ha mostrado un trabajo completo para que cada paso sea explícito. (Recuerde que en la resolución de ecuaciones de magnitud log se refiere a logaritmos a base 10 y no logaritmos naturales o ln.)
Ejemplo 4: dados m Y M, Encontrar D.
Betelgeuse tiene una magnitud aparente de 0.45 y una magnitud absoluta de -5.14. ¿Qué tan lejos está?
este problema requiere que reescribamos la ecuación 4.2 Para darnos d como desconocido., Esto se muestra a continuación:
que puede ser escrito como:
ahora sustituyendo en:
así que Betelgeuse es de unos 130 pc distante.
de nuevo, este ejemplo muestra el trabajo completo, mientras que en realidad es posible que no muestre cada paso., Es importante, sin embargo, que establezca su trabajo a tales problemas claramente para que pueda comprobar su manipulación algebraica y sus sustituciones. Trabajar con registros e índices puede ser complicado, así que asegúrese de saber cómo hacerlo en su calculadora.
Ejemplo 5: dados M Y d, encuentra m.
en la práctica este tipo de problema es menos realista para objetos reales, ya que normalmente podemos medir sus magnitudes aparentes directamente, sin embargo, puede ser que deseemos calcular la magnitud aparente que una clase o tipo de objeto puede haber dado a los otros parámetros. De nuevo, comenzando con la ecuación 4.,3 determinemos qué tan brillante aparecería una supergigante como Deneb con una magnitud absoluta de -8.73 si estuviera a 230 pársecs de distancia.
por lo que sustituyendo en:
así que Deneb tendría una magnitud aparente de -1.89. Esto lo haría más brillante en nuestro cielo nocturno que Sirio (m = -1.44)., En realidad Deneb es alrededor de 990 PC distante aunque este valor tiene una gran incertidumbre.
Ejemplo 6: ¿Qué pasa si no se da d pero se da paralaje, p?
Esto es realmente muy sencillo. Recordemos de la sección Sobre astrometría que hay una relación directa entre la distancia y el paralaje.
así que simplemente necesita insertar esto en la ecuación 4.2 o 4.3.
Naming& Identifying Stars
háganos saber volver a visitar esa foto de Crux y los punteros de la parte superior de esta página., La foto de abajo muestra la misma región con las estrellas prominentes etiquetadas. También se muestran sus magnitudes aparentes. Crux es una constelación, una de las 88 regiones en las que la esfera celeste ha sido dividida y acordada internacionalmente por los astrónomos. Crux es en realidad la más pequeña de las constelaciones y se identifica fácilmente en los cielos del Sur. Las prominentes estrellas cercanas comúnmente llamadas punteros son en realidad parte de una gran constelación llamada Centauro.

ahora puede notar que las estrellas se nombran usando letras del alfabeto griego; α, β, γ δ y ε (Alfa, beta, gamma, delta, epsilon son las primeras cinco) seguidas por la abreviatura estándar de tres letras para cada constelación (Cru para Crucis o Crux y Cen para Centauro). Si observas de cerca las magnitudes aparentes de las cinco estrellas nombradas en el punto crucial, verás que la estrella más brillante está etiquetada como α, la siguiente β y así sucesivamente., Este sistema se llama el sistema de Bayer, después de Johann Bayer que lo introdujo en 1603. A la estrella más brillante de una constelación se le asigna la letra α, la siguiente β y así sucesivamente. Una excepción a esta regla es &alpha Orionis o Betelgeuse. De hecho, es más débil que β Ori, Rigel por una pequeña cantidad. Este es un caso histórico interesante resuelto por la realización de que Betelgeuse ha atenuado ligeramente en brillo desde que fue nombrado bajo el sistema Bayer.,
un punto a recordar sobre las constelaciones es que las estrellas dentro de una constelación no suelen estar asociadas físicamente entre sí, a diferencia de las estrellas en cúmulos. El hecho de que aparezcan juntos es puramente un efecto de alineación a lo largo de la línea de visión del recorrido. De hecho, las estrellas en la región de arriba están ampliamente separadas en distancia de nosotros como se muestra en la siguiente imagen.
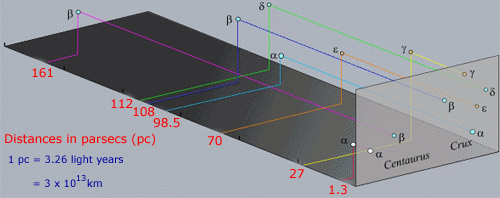
algunas de las estrellas brillantes como α Cen también tienen su propio nombre específico. Sirius (α Sco) es uno de esos ejemplos, mientras que α Cen también se llama Rigel Kentaurus. Muchos nombres de estrellas son de origen árabe de la época en que los registros griegos fueron preservados y desarrollados por astrónomos islámicos. El problema con el sistema Bayer de nombrar estrellas es que solo hay 24 letras en el alfabeto griego, pero hay muchas más estrellas que en cada constelación.
La mayoría de las estrellas, de hecho, no tienen un nombre específico o una clasificación Bayer., En estos días los astrónomos han compilado vastos catálogos de estrellas, algunas con más de 10 millones de objetos, por lo que la mayoría de las estrellas solo tienen un número de catálogo. Las estrellas pueden tener muchos más de un nombre de identificación o número de catálogo, dependiendo del número de catálogos en los que se encuentren. La estrella variable, δ Cep, por ejemplo, también se conoce como HIP 110991, SAO 34508, o cualquiera de los más de 30 identificadores. Muchos catálogos utilizan coordenadas celestes como ascensión recta y declinación para identificar objetos. Así, δ Cep se conoce como IRAS 22273 + 5809, CCDM J22292+5825a y AAVSO 2225+57., Las ligeras variaciones en RA y dec para los catálogos surgen debido al Movimiento Propio de las estrellas y la precesión del marco de referencia.