hypotesprövning

huvudsyftet med statistiken är att testa en hypotes. Till exempel kan du köra ett experiment och upptäcka att ett visst läkemedel är effektivt vid behandling av huvudvärk. Men om du inte kan upprepa experimentet, kommer ingen att ta dina resultat på allvar. Ett bra exempel på detta var cold fusion discovery, som petered i dunkel eftersom ingen kunde duplicera resultaten.,

titta på videon för en kort översikt över hypotesprovning, eller läs vidare nedan:

innehåll (Klicka för att hoppa till avsnittet):

1. Vad är en hypotes?
2. Vad är hypotesprovning?
3. Hypotesprovningsexempel (ett prov Z-Test).
4. hypotestest på ett medelvärde (TI 83).
5. Bayesian hypotesprövning.
6. fler Hypotesprovningsartiklar

Se även:

• hypotesprov i en bild
• kritiska värden
• Vad är nollhypotesen?,

behöver du hjälp med ett läxproblem? Kolla in vår handledning sida!

Vad är en hypotes?

En hypotes är en utbildad gissning om något i världen omkring dig. Det bör vara testbart, antingen genom experiment eller observation. Till exempel:

• ett nytt läkemedel som du tror kan fungera.
• ett sätt att undervisa du tror kan vara bättre.,
• en möjlig plats för nya arter.
• ett rättvisare sätt att administrera standardiserade tester.

det kan verkligen vara något alls så länge du kan sätta det på prov.

Vad är en hypotes uttalande?

om du ska föreslå en hypotes är det vanligt att skriva ett uttalande. Ditt uttalande kommer att se ut så här:
” om jag…(gör detta till en oberoende variabel)….då (detta kommer att hända med den beroende variabeln).”
till exempel:

• Om jag (minska mängden vatten som ges till örter) då (örterna kommer att öka i storlek).,
• Om jag (ge patienter rådgivning förutom medicinering) då (deras totala depression skala kommer att minska).
• Om jag (ge tentor vid middagstid i stället för 7) Då (student testresultat kommer att förbättras).
• Om jag (titta på denna viss plats) då (jag är mer benägna att hitta nya arter).

en bra hypotes uttalande bör:

• inkludera en ”if” och ”then” uttalande (enligt University of California).
• inkluderar både oberoende och beroende variabler.
• testas genom experiment, undersökning eller annan vetenskapligt sund teknik.,
• baseras på information i tidigare forskning (antingen din eller någon annans).
• har konstruktionskriterier (för teknik-eller programmeringsprojekt).

Vad är hypotesprovning?

hypotesprövning i statistik är ett sätt för dig att testa resultaten av en undersökning eller ett experiment för att se om du har meningsfulla resultat. Du testar i princip om dina resultat är giltiga genom att räkna ut oddsen att dina resultat har hänt av en slump., Om dina resultat kan ha hänt av en slump, experimentet kommer inte att vara repeterbar och så har liten användning.

hypotesprövning kan vara en av de mest förvirrande aspekterna för studenter, för det mesta för att innan du ens kan utföra ett test måste du veta vad din nollhypotes är. Ofta kan de knepiga ordproblemen som du står inför vara svåra att dechiffrera., Men det är lättare än du tror; allt du behöver göra är:

1. räkna ut din nollhypotes,
2. ange din nollhypotes,
3. Välj vilken typ av test du behöver utföra,
4. antingen stödja eller avvisa nollhypotesen.

Vad är nollhypotesen?

om du spårar vetenskapens historia är nollhypotesen alltid det accepterade faktumet. Enkla exempel på nollhypoteser som allmänt accepteras som sanna är:

1. DNA är formad som en dubbel helix.
2. Det finns 8 planeter i solsystemet (exklusive Pluto).,
3. att ta Vioxx kan öka risken för hjärtproblem (ett läkemedel som nu tas bort från marknaden).

hur anger jag nollhypotesen?

Du kommer inte att behöva faktiskt utföra ett riktigt experiment eller undersökning i elementär statistik (eller till och med motbevisa ett faktum som ”Pluto är en planet”!), så du får ordproblem från verkliga situationer. Du måste ta reda på vad din hypotes är från problemet. Detta kan vara lite svårare än att bara räkna ut vad det accepterade faktumet är. Med ord problem, du letar efter att hitta ett faktum som är ogiltig (dvs, något du kan avvisa).

hypotesprövning exempel # 1: Grundläggande exempel

en forskare tror att om knäoperationspatienter går till fysioterapi två gånger i veckan (istället för 3 gånger) kommer deras återhämtningsperiod att vara längre. Genomsnittliga återhämtningstider för knäoperationspatienter är 8,2 veckor.

hypotesen i denna fråga är att forskaren anser att den genomsnittliga återhämtningstiden är mer än 8,2 veckor. Det kan skrivas i matematiska termer som:
H1: μ> 8.,2

därefter måste du ange nollhypotesen (se: hur man anger nollhypotesen). Det är vad som händer om forskaren har fel. I ovanstående exempel, om forskaren har fel är återhämtningstiden mindre än eller lika med 8,2 veckor. I matematik är det:
H0 μ ≤ 8.2

avvisa nollhypotesen

För tio år sedan trodde vi att det fanns 9 planeter i solsystemet. Pluto degraderades som en planet 2006. Nollhypotesen om ” Pluto är en planet ”ersattes av” Pluto är inte en planet.,”Naturligtvis är det inte alltid så lätt att avvisa nollhypotesen—den hårda delen brukar räkna ut vad din nollhypotes är i första hand.

Hypotesprovsexempel (ett prov Z-Test)

ett prov z-testet används inte så ofta (eftersom vi sällan känner till den faktiska populationsstandardavvikelsen). Det är dock en bra idé att förstå hur det fungerar eftersom det är en av de enklaste testerna du kan utföra i hypotesprovning., I engelska klassen fick du lära dig grunderna (som grammatik och stavning) innan du kunde skriva en historia; tänk på ett prov z-test som grunden för att förstå mer komplex hypotesprovning. Denna sida innehåller två hypotesprovningsexempel för ett prov z-test.

ett exempel på hypotesprövning: #2

en rektor vid en viss skola hävdar att eleverna i hans skola är över genomsnittet intelligens. Ett slumpmässigt urval av trettio studenter IQ poäng har en genomsnittlig poäng på 112., Finns det tillräckliga bevis för att stödja huvudmannens påstående? Medelpopulationen IQ är 100 med en standardavvikelse på 15.

Steg 1: ange nollhypotesen. Det accepterade faktum är att befolkningens medelvärde är 100, så: H0: μ=100.

steg 2: Ange den alternativa hypotesen. Påståendet är att eleverna har över genomsnittliga IQ-poäng, så:
H1: μ> 100.
det faktum att vi letar efter poäng ”större än” en viss punkt innebär att detta är en en-tailed test.

steg 3: rita en bild som hjälper dig att visualisera problemet.,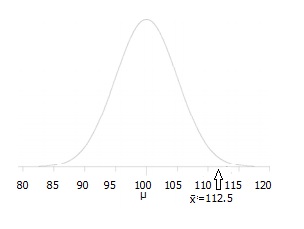

steg 4: Ange alfanivån. Om du inte får en alfa-nivå, Använd 5% (0.05).

Steg 5: Hitta avvisningsområdet (angivet av din alfanivå ovan) från z-tabellen. Ett område av .05 är lika med en z-poäng på 1.645.

steg 6: hitta teststatistiken med denna formel: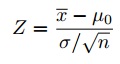
för denna uppsättning data: z= (112.5 – 100) / (15/√30) = 4.56.

steg 6: om Steg 6 är större än Steg 5, avvisa nollhypotesen., Om det är mindre än Steg 5 kan du inte avvisa nollhypotesen. I det här fallet är det större (4.56> 1.645), så du kan avvisa null.

ett exempel på hypotesprövning: #3

blodglukosnivåer för överviktiga patienter har i genomsnitt 100 med en standardavvikelse på 15. En forskare tror att en diet som är hög i rå majsstärkelse kommer att ha en positiv eller negativ effekt på blodsockernivån., Ett urval av 30 patienter som har provat den råa majsstärkelsedieten har en genomsnittlig glukosnivå på 140. Testa hypotesen att den råa majsstärnan hade en effekt.

* denna process görs mycket enklare om du använder en TI-83 eller Excel för att beräkna z-poängen (det”kritiska värdet”).,
Se:

• kritiskt z-värde TI 83
• z-poäng i Excel

hypotesprövning exempel: medelvärde (med TI 83)

Du kan använda TI 83-kalkylatorn för hypotesprövning, men räknaren kommer inte att räkna ut null och alternativa hypoteser; det är upp till dig att läsa frågan och mata in den i räknaren.

exempel problem: ett urval av 200 personer har en medelålder på 21 med en befolkning standardavvikelse (σ) av 5. Testa hypotesen att befolkningens medelvärde är 18,9 vid α = 0,05.

Steg 1: Ange nollhypotesen., I det här fallet är nollhypotesen att befolkningens medelvärde är 18,9, så vi skriver:
H0: μ = 18,9

steg 2: Ange den alternativa hypotesen. Vi vill veta om vårt prov, som har ett medelvärde på 21 istället för 18,9, verkligen skiljer sig från befolkningen, därför vår alternativa hypotes:
H1: μ, 18,9

steg 3: Tryck på Stat och tryck sedan på högerpilen två gånger för att välja test.

steg 4: Tryck på 1 för att välja 1: Z-Test…. Tryck på ENTER.

Steg 5: använd högerpilen för att välja statistik.

steg 6: Ange data från problemet:
μ0: 18.,9
σ: 5
x: 21
n: 200
μ: μ0

Steg 7: pil ner för att beräkna och trycka på ENTER. Kalkylatorn visar p-värdet:
p = 2.87 × 10-9

detta är mindre än vårt alfavärde för .05. Det innebär att vi bör avvisa nollhypotesen.

Bayesian Hypothesis Testing: Vad är det?

Bayesian hypotesprövning hjälper till att svara på frågan:kan resultaten från ett test eller en undersökning upprepas?
Varför bryr vi oss om ett test kan upprepas?, Låt oss säga att tjugo personer i samma by kom ner med leukemi. En grupp forskare tycker att mobilmaster är skyldiga. En andra studie visade dock att mobiltornen inte hade något att göra med cancerklustret i byn. Faktum är att de fann att cancersna var helt slumpmässiga. Om det låter omöjligt, kan det faktiskt hända! Kluster av cancer kan hända helt enkelt av en slump. Det kan finnas många anledningar till varför den första studien var felaktig., En av de främsta anledningarna kan vara att de bara inte tog hänsyn till att ibland saker händer slumpmässigt och vi vet bara inte varför.

P-Värden.

det är bra vetenskap att låta folk veta om dina studieresultat är solida, eller om de kunde ha hänt av en slump. Det vanliga sättet att göra detta är att testa dina resultat med ett p-värde. Ett p-värde är ett tal som du får genom att köra ett hypotestest på dina data. Ett p-värde på 0,05 (5%) eller mindre är vanligtvis tillräckligt för att hävda att dina resultat är repeterbara., Det finns dock ett annat sätt att testa giltigheten av dina resultat: Bayesian hypotesprövning. Denna typ av testning ger dig ett annat sätt att testa styrkan i dina resultat.

Bayesian hypotesprövning.

traditionell testning (den typ du förmodligen kom över i elementär statistik eller AP statistik) kallas icke-bayesiska. Det är hur ofta ett resultat händer över upprepade körningar av experimentet. Det är en objektiv bild av om ett experiment är repeterbart.
Bayesian hypotesprövning är en subjektiv syn på samma sak., Det tar hänsyn till hur mycket tro du har i dina resultat. Med andra ord, skulle du satsa pengar på resultatet av ditt experiment?

skillnader mellan traditionell och bayesisk hypotesprovning.

traditionell testning (Non Bayesian) kräver att du upprepar provtagning om och om igen, medan Bayesian testning inte gör det. Den huvudsakliga skillnaden mellan de två är i det första steget av testning: anger en sannolikhetsmodell. I Bayesian testning lägger du till förkunskaper till detta steg., Det kräver också användning av en bakre Sannolikhet, vilket är den villkorliga sannolikheten som ges till en slumpmässig händelse efter att alla bevis har beaktats.

argument för Bayesiansk testning.

många forskare tror att det är ett bättre alternativ till traditionell testning, eftersom det:

1. innehåller förkunskaper om data.
2. tar hänsyn till personliga övertygelser om resultaten.

argument mot.

1. inklusive tidigare data eller kunskap är inte motiverat.
2. Det är svårt att beräkna jämfört med icke-bayesisk testning.,

tillbaka till toppen

hypotestest artiklar

grunderna:

1. Vad är Ad Hoc-testning?
2. Komposithypotestest
3. Vad är en Avstötningsregion?
4. Vad är ett Tvåstjärtat Test?
5. hur man bestämmer om ett hypotestest är ett ett Tailed Test eller ett två Tailed Test.
6. hur man bestämmer om en hypotes är ett Vänstersvansat Test eller ett Högersvansat Test.
7. hur man anger nollhypotesen i statistiken.
8. hur man hittar ett kritiskt värde.
9. hur man stöder eller avvisar en nollhypotes.,

specifika tester:

1. ANOVA.
2. Brunner Munzel Test (generaliserat Wilcoxon Test)
3. Chi Square Test för normalitet
4. Cochran-Mantel-Haenszel Test
5. f Test
6. Granger Causality Test.
7. Hotelling S t-Squared
8. Kpss Test.
9. Vad är ett Sannolikhetsförhållande Test?
10. Log rank test.
11. MANCOVA
12. sekventiellt Sannolikhetsförhållande Test
13. hur man kör ett Teckentest.
14. t Test: ett prov.
15. t-Test: två prov.
16. Welchs ANOVA.
17. Welchs Test för ojämlika variationer.,
18. Z-Test: ett prov.
19. z Test: två andel
20. Wald Test.

1. Vad är en Acceptansregion?
2. hur man beräknar Chebyshevs teorem.
3. beslutsregel.
4. frihetsgrader.
5. Riktningstest
6. False Discovery Rate
7. hur man beräknar den minst signifikanta skillnaden.
8. nivåer i statistiken.
9. hur man beräknar felmarginal.
10. genomsnittlig skillnad (skillnad i medel)
11. problemet med flera tester.
12. Vad är Neyman-Pearson Lemma?
13. ett Mediantest för prov.,
14. REGWF
15. hur man hittar en provstorlek (Allmänna instruktioner).
16. Sig 2(Tailed) betyder i resultat
17. Vad är en standardiserad teststatistik?
18. så här hittar du standardfel
19. standardiserade värden: exempel.
20. hur man beräknar en T-poäng.
21. t-poäng Vs. A Z. poäng.
22. testa ett enda medelvärde.
23. ojämna provstorlekar.
24. enhetligt mest kraftfulla tester.
25. hur man beräknar en Z-poäng.

——————————————————————————

behöver du hjälp med en läxa eller testfråga?, Med Chegg Study kan du få steg-för-steg-lösningar på dina frågor från en expert på området. Din första 30 minuter med en Chegg handledare är gratis!