The colors of the body of the table illustrate the number of ways to throw each total., Sannolikheten att kasta någon given total är antalet sätt att kasta den totala dividerat med det totala antalet kombinationer (36). I följande tabell visas det specifika antalet sätt att kasta varje total och sannolikheten för att kasta den totala.

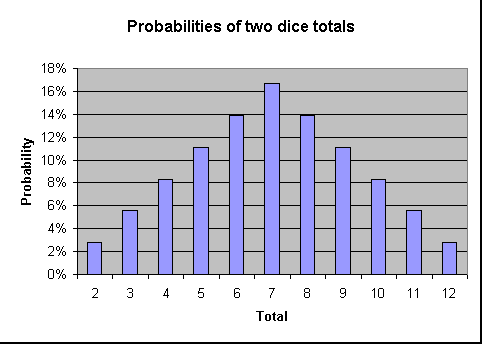
följande visar sannolikheten att kasta varje total i ett diagramformat. Som diagrammet visar ju närmare summan är till 7 desto större är sannolikheten för att den kastas.,

Fältinsatsexempel

nu när vi förstår sannolikheten att kasta varje total kan vi tillämpa denna information på tärningsspel i kasinon för att beräkna husets kant. Tänk till exempel på fältinsatsen i craps. Detta spel betalar 1:1 (jämna pengar) om nästa kast är en 3, 4, 9, 10, eller 11, 2:1 (dubbla insatsen) på 2, och 3:1 (tredubbla insatsen) på 12. Observera att det finns 7 summor som vinner och endast 4 som förlorar vilket kan orsaka någon som inte visste bättre att tro att det var en bra chansning.,

spelarens retur kan definieras som summan av produkterna av sannolikheten för varje händelse och nettoretur för den händelsen. Följande tabell visar varje möjlig total, nettoavkastningen, sannolikheten att kasta den totala och den genomsnittliga avkastningen. Den genomsnittliga avkastningen är produkten av nettoavkastningen och sannolikheten. Spelarens avkastning är summan av den genomsnittliga avkastningen.

den sista raden visar spelarens återgång till be -.0278, med andra ord för varje $ 1 satsning spelaren kan förvänta sig att förlora 2,78 cent., Spelarens förlust är husets vinst så husets kant är produkten av -1 och spelarens avkastning, i detta fall 0.0278 eller 2.78%.

för sannolikheterna i summan av mer än två tärningar se mina sannolikheter för 1 till 25 tärningar avsnitt.

skriven av: Michael Shackleford