• historisk bakgrund
• skenbar magnitud, m
• absolut magnitud, M
• hitta Avståndet till stjärnor-Avståndsmodulen
• magnitud / avståndsberäkningar
• namnge & identifiera stjärnor

studera stjärnfältfotografin nedan. Det visar en region av himlen runt konstellationen Crux, vanligen kallad Södra korset. Flytta markören över fotot för att identifiera några stjärnor.

vilken stjärna är ljusaste?,

om du svarade Alpha (α) Centauri, stjärnan längst ner till vänster på fotografiet du har rätt. Som du kan se visar en fotografisk bild som denna många fler stjärnor än du kan se med ditt blotta öga. Men vissa stjärnor är mer framträdande än andra. Genom att välja α Centauri gjorde du några antaganden. Vad var de?

ett fotografi som detta visar ljusa stjärnor som större diskar än ljussvagare stjärnor., Betyder det att dessa stjärnor är fysiskt större än de svagare stjärnorna på bilden? Kom ihåg att i avsnittet om astrometri lärde vi oss att alla andra stjärnor än vår sol är så avlägsna att de effektivt är punktkällor. Varför verkar vissa ljusare (för våra ögon) eller större (i fotografier) än andra? Vad är faktiskt ljusstyrka och hur kan vi mäta det? Svaren på dessa frågor utgör fokus för detta avsnitt.,

historisk bakgrund

konceptet att mäta och jämföra stjärnornas ljusstyrka kan spåras tillbaka till den grekiska astronomen och matematikern Hipparchus (190 – 120 f.Kr.). En av de största astronomerna i antiken, han krediteras med att producera en katalog av 850 stjärnor med positioner och jämförande ljus., I hans system tilldelades de ljusaste stjärnorna en magnitud på 1, den näst ljusaste magnituden 2 och så vidare till de svagaste stjärnorna, bara synliga för blotta ögat som var magnitud 6. Denna sexpunktsskala kan ses som en rankning, förstklassiga stjärnor, de ljusaste, var första magnituden och dim lågfrekventa stjärnor var sjätte magnituden.

upptäckten av ljussvagare stjärnor med teleskop i början av 1600-talet krävde att skalan skulle utvidgas utöver magnitud 6., Utvecklingen av visuella fotometrar, instrument för att mäta stjärnintensiteter, på 1800-talet av John Herschel och andra, föranledde astronomerna att anta en internationell standard. Det faktum att ögonen upptäcker skillnader i intensitet logaritmiskt snarare än linjärt upptäcktes på 1830-talet. år 1856 föreslog Norman Pogson att en stjärna av magnitud 1 var 100 × ljusare än en stjärna av magnitud 6. En skillnad av en storlek var därför lika med 5√100 = 2,512 gånger i ljusstyrka.,

skenbar magnitud, m

skenbar magnitud, m, av en stjärna är den magnitud den har sett av en observatör på jorden.

ett mycket ljust objekt, som solen eller månen kan ha en negativ skenbar magnitud. Även om Hipparchus ursprungligen tilldelade de ljusaste stjärnorna att ha en magnitud på 1 mer noggrann jämförelse visar att den ljusaste stjärnan på natthimlen, Sirius eller α Canis Majoris (CMA) faktiskt har en skenbar magnitud på m = -1,44. Med omkalibreringen av Hipparchus ursprungliga värden är den ljusa stjärnan Vega nu definierad för att ha en skenbar magnitud på 0.0.,

efter den teleskopiska upptäckten av ljussvaga stjärnor i början av 1600-talet har magnitudskalan också varit tvungen att utvidgas till föremål som är ljussvagare än magnitud 6. Tabellen nedan visar omfattningen av uppenbara magnituder för himmelska föremål.

objekt	skenbar magnitud
Sun	-26.5
fullmåne	-12.5
Venus	-4.,3
Mars or Jupiter	-2
Sirius (α CMa)	-1.44
Vega (α Lyr)	0.0
Alnair (α Gru)	1.73
Naked-eye limit	6.5
Binocular limit	10
Proxima Cen	11.,09
Visual limit through 20 cm telescope	14
QSO at redshift z = 2	≈ 20
Cepheid in galaxy M100 observed with HST	26
Galaxy at z = 6 observed with Gemini 8.1 m telescope	28
Limit for James Webb Space Telescope	≥ 30

If a star of magnitude 1 is 2.,512 × ljusare än en stjärna av magnitud 2 och 100 &gånger ljusare än en sjätte magnitud stjärna hur mycket ljusare är det än en stjärna av magnitud 3? Du måste vara försiktig här. Det är inte bara 2 × 2.512 olika. Du måste komma ihåg att en skillnad på en storlek är lika med 5√100 = 2,512. En skillnad på 2 magnituder = därför 2.5122 = 6.31 × skillnad i ljusstyrka.

två objekt av olika magnituder varierar därför i ljusstyrka med 2.512 höjt till effekten av dig magnitud skillnad., Om vi skriver detta som en ekvation ges förhållandet mellan ljusstyrka eller intensitet, IA/ib mellan två objekt, A och B, med magnituder mA och mB med följande ekvation:

låt oss ta en titt på ett exempel.

exempel 1: jämföra två stjärnor.
hur mycket ljusare är Alnair, skenbar magnitud på +1,73 än Proxima Cen med en magnitud på 11,09?
använda ekvation 4.1 vi har:

så, ersätta i:

exempel 2: Hur mycket ljusare är solen än fullmånen?
för detta minns vi från tabellen ovan att solen har en skenbar magnitud på -26,5 och fullmånen, – 12,5.

så med ekvation 4.1 får vi:

att ersätta i ger oss:

det är viktigt att komma ihåg att storleken helt enkelt är ett tal, Det har inga enheter. Symbolen för skenbar magnitud är ett lägre fall m; Du måste göra detta klart i alla problem.

absolut magnitud, m

vad betyder det faktum att Sirius har en skenbar magnitud på -1,44 och Betelgeuse en skenbar magnitud på 0,45 berätta om dessa två stjärnor? Ett annat sätt att tänka på detta är att fråga Varför är Sirius den ljusaste stjärnan på natthimlen?, En stjärna kan verka ljus av två huvudskäl:

1. Det kan vara naturligt lysande, det vill säga det kan vara en kraftfull emitter av elektromagnetisk strålning, eller
2. Det kan vara mycket nära oss, eller båda.

skenbar magnitud av en stjärna beror därför delvis på dess avstånd från oss. I själva verket Sirius verkar ljusare än Betelgeuse just eftersom Sirius är mycket nära oss, endast 2.6 pc bort medan Betelgeuse är ca 160 pc avlägsen., Insikten om att Stjärnor inte alla har samma ljusstyrka innebar att enbart skenbar magnitud inte var tillräckligt för att jämföra stjärnor. Ett nytt system som skulle göra det möjligt för astronomer att direkt jämföra stjärnor utvecklades. Detta system kallas den absoluta magnituden, M.

den absoluta magnituden, M, av en stjärna är den magnitud som stjärnan skulle ha om den var på ett avstånd av 10 parsek från oss. Ett avstånd på 10 pc är rent godtyckligt men nu internationellt överenskommet av astronomer., Skalan för absolut magnitud är densamma som för skenbar magnitud, det vill säga en skillnad på 1 magnitud = 2,512 gånger skillnad i ljusstyrka. Denna logaritmiska skala är också öppen och unitless. Återigen, ju lägre eller mer negativa värdet av M, desto ljusare är stjärnan. Absolut storlek är ett bekvämt sätt att uttrycka luminositeten hos en stjärna. När den absoluta storleken på en stjärna är känd kan du också jämföra den med andra stjärnor. Betelgeuse, m = -5.6 är inneboende mer lysande än Sirius med en m = 1,41.

vår sol har en absolut visuell magnitud på 4,8.,

hitta Avståndet till stjärnor – avstånd modul

som ni kanske minns från avsnittet om astrometri, de flesta stjärnor är för avlägsen för att få deras parallax mätt direkt. Men om du vet både de uppenbara och absoluta magnituderna för en stjärna kan du bestämma avståndet. Låt oss titta igen på Sirius och Betelgeuse plus en annan stjärna som heter gj 75.

hur långt bort är gj 75? Det är en ovanlig stjärna genom att dess uppenbara och absoluta magnituder är desamma. Varför? Anledningen är att det faktiskt är 10 parsecs långt ifrån oss, så per definition måste dess två storheter vara desamma.,

hur är det med Sirius? Dess skenbara magnitud är lägre (därför ljusare) än dess absoluta magnitud. Detta innebär att det är närmare än 10 parsek till oss. Betelgeuse skenbar magnitud är högre (därför dimmer) än dess absoluta magnitud så det skulle verka ännu ljusare i natthimlen om det bara var 10 parsecs avlägsen.

astronomer använder skillnaden mellan skenbar och absolut magnitud, avståndsmodulen, som ett sätt att de benämner avståndet till en stjärna.

• Distance Modulus = m – M.
• Distance modulus är negativ för stjärnor närmare än 10 parsecs.,
• Avståndsmodulen är positiv för stjärnor längre bort än 10 parsecs.
• storleken på avståndsmodulen bestämmer det faktiska värdet av avståndet, så att en stjärna av avståndsmodulen 1.5 är närmare än en med en avståndsmodul på 8,7.

magnitud/avståndsberäkningar

avståndsmodulen kan användas för att bestämma avståndet till en stjärna med hjälp av ekvationen:

där d är i parsek. Observera att om d = 10 pc är M och M desamma. (En formell härledning av denna ekvation ges på Nästa sida om ljusstyrka)., Den NSW HSC kursplan formel blad ger ekvationen som:

men detta är helt enkelt en omarbetning av ekvation 4.2. Du borde vara bekväm med att lösa denna ekvation med tanke på två av de tre variablerna. Låt oss veta titta på hur du kan lösa några exempel.

Exempel 3: med Tanke på m och d, måste hitta M.
β Crucis (eller Mimosa) har en skenbar magnitud på 1,25 och är 108 parsek avlägsen. Vad är dess absoluta storlek?

använda ekvation 4.3 vi har:

så β Crucis har en absolut magnitud på -3.92
observera denna beräkning har visat fullt fungerande så att varje steg är explicit. (Kom ihåg att lösa magnitud ekvationer log avser logaritmer till bas 10 och inte naturliga logaritmer eller ln.)

exempel 4: givet m och M, hitta D.
Betelgeuse har en skenbar magnitud på 0,45 och en absolut magnitud på -5,14. Hur långt bort är det?
detta problem kräver att vi skriver om ekvation 4.2 för att ge oss d som det okända., Detta visas nedan:

som kan skrivas som:

ersätter nu i:

så Betelgeuse är ca 130 pc avlägsen.

återigen visar det här exemplet komplett arbete medan du i verkligheten kanske inte visar varje steg., Det är dock viktigt att du ställer in ditt arbete på sådana problem tydligt så att du kan kontrollera din algebraiska manipulation och dina substitutioner. Arbeta med loggar och index kan vara knepigt så se till att du vet hur man gör dessa på din räknare.

exempel 5: med tanke på M och d, hitta m.
i praktiken är denna typ av problem mindre realistiskt för faktiska objekt eftersom vi normalt kan mäta deras skenbara magnituder direkt men det kan vara så att vi vill beräkna vilken skenbar magnitud en klass eller typ av objekt kan ha gett de andra parametrarna. Återigen, börjar med ekvation 4.,3 Låt oss bestämma hur ljus en supergiant som Deneb med en absolut storlek på -8.73 skulle dyka upp om det var 230 parsecs bort.

så ersätter i:

-8.7 + 5*1.3617

så Deneb skulle ha en skenbar magnitud på -1,89. Detta skulle göra det ljusare i vår natthimlen än Sirius (m = -1,44)., I verkligheten är Deneb ca 990 pc avlägsen även om detta värde har en stor osäkerhet.

exempel 6: Vad händer om d inte ges men parallax, p ges?
Detta är faktiskt mycket rakt fram. Minns från avsnittet om astrometri att det finns ett direkt samband mellan avstånd och parallax.

så du behöver bara infoga detta i ekvation 4.2 eller 4.3.

namnge& identifiera stjärnor

låt oss veta återbesök detta foto av Crux och pekare från toppen av denna sida., Bilden nedan visar samma region med de framträdande stjärnorna märkta. De har också sina uppenbara storheter visat. Crux är en konstellation, en av 88 regioner som den himmelska sfären har brutits upp i och överenskommits internationellt av astronomer. Crux är faktiskt den minsta av konstellationerna och identifieras lätt i södra himlen. De framträdande närliggande stjärnorna som vanligen kallas pekare är faktiskt en del av en stor konstellation som heter Centaurus.

Nu kanske du märker att stjärnorna är namngivna med bokstäver från det grekiska alfabetet; α, β, γ δ och ε (alpha, beta, gamma, delta, epsilon är de första fem) följt av standard förkortning med tre bokstäver för varje konstellation (Cru för Crucis eller springande Punkten och Cen för Centaurus). Om man tittar närmare på de skenbara magnituderna för de fem namngivna stjärnorna i Crux ser man att den ljusaste stjärnan är märkt α, nästa β Och så vidare., Detta system kallas Bayer-systemet, efter Johann Bayer som introducerade det 1603. Den ljusaste stjärnan i en konstellation tilldelas bokstaven α, nästa β och så vidare. Ett undantag från denna regel är &alpha Orionis eller Betelgeuse. Det är faktiskt svagare än β Ori, Rigel med en liten mängd. Detta är ett intressant historiskt fall löst genom att inse att Betelgeuse har dämpat något i ljusstyrka eftersom det namngavs under Bayer-systemet.,

en punkt att komma ihåg om konstellationer är att stjärnorna i en konstellation vanligtvis inte är fysiskt associerade med varandra, till skillnad från stjärnor i kluster. Det faktum att visas nära varandra är rent en anpassningseffekt längs turlinjen. Faktum är att stjärnorna i regionen ovan är brett åtskilda på avstånd från oss som visas i nästa bild.

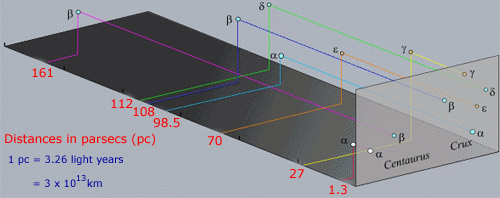
några av de ljusa stjärnorna som α Cen har också sitt eget specifika namn. Sirius (α Sco) är ett sådant exempel, medan α Cen kallas också Rigel Kentaurus. Många stjärnnamn är arabiska ursprung från den tid då grekiska poster bevarades och utvecklades av islamiska astronomer. Problemet med Bayer-systemet för att namnge stjärnor är att det bara finns 24 bokstäver i det grekiska alfabetet men det finns många fler stjärnor än i varje konstellation.

de flesta stjärnor har faktiskt inte ett specifikt namn eller Bayer-klassificering., Idag har astronomer sammanställt stora kataloger av stjärnor, några med över 10 miljoner objekt, så de flesta stjärnor har bara ett katalognummer. Stjärnor kan ha många fler än ett identifieringsnamn eller katalognummer, beroende på antalet kataloger de är i. Variabla stjärnor, δ Cep till exempel är också känd som HIP 110991, SAO 34508, eller någon av de mer än 30 andra kännetecken! Många kataloger använder himmelska koordinater som rätt uppstigning och deklination för att identifiera objekt. Alltså δ Cep är känd som IRAS 22273+5809, CCDM J22292+5825A och AAVSO 2225+57., De små variationerna i RA och dec för katalogerna uppstår på grund av stjärnornas korrekta rörelse och precessionen av referensramen.