ACT Math Practice

du får använda en kalkylator för dessa frågor. Du kan använda din kalkylator för eventuella problem du väljer, men några av problemen kan bäst göras utan att använda en kalkylator.

1. Vad är det största värdet av x som löser ekvationen x 2 – 4x + 3 = 0

(A) 1 (B) 2 (c) 3 (D) 4 (E) 5
se svaret

svar: (g)
om du har en bit information om en cirkel kan du hitta allt annat du behöver., Området av cirkel A är 16π och eftersom A = π r 2 , radien av cirkel A måste vara 4. Om cirkelns radie B är hälften av cirkel A, måste cirkelns radie B vara 2. Hitta sedan omkretsen av cirkel B , med C = 2π r = 2π r(2) = 4π, eller val (G).

se svaret

3. I ordet hökar, hur många sätt är det möjligt att omorganisera bokstäverna om ingen upprepar och bokstaven W måste gå sist?

(a) 5 (B) 15 (C) 24 (D) 120 (e) 650

se svaret

4., Vad är lutningen på linjen representerad av ekvationen 10 x + 2 x = y + 6 ?
(F) 10 (G) 12 (H) 14 (J) 15 (K) 16

se svaret

5. I triangeln ABC nedan är tan av den markerade vinkeln lika med

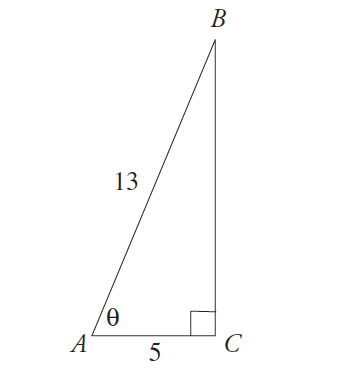
(a) 5 12 12 (B) 12 13 (C) 17 12 (D) 12 5 (E) 3

svar: (D)
Använd ekvationen tangent = motsatt / angränsande. Din första impuls här kan vara att lösa för den okända sidan, men ta en närmare titt på var den markerade vinkeln är., Dess intilliggande sida är 5, vilket betyder att tangenten för den vinkeln måste ha en nämnare på 5. Endast (D) har det, så det är det enda svaret som kan fungera. Om du löser för den okända sidan, kom ihåg dina Pythagoras tripplar: det här är en 5:12:13 triangel, så den okända sidan måste vara 12.

se svaret