frecvența cumulativă

• Exemplul 1 – variabile Discrete
• Exemplul 2 – variabile continue
• alte calcule de frecvență cumulative

frecvența cumulativă este utilizată pentru a determina numărul de observații care se află deasupra (sau sub) unei anumite valori dintr-un set de date. Frecvența cumulată este calculată folosind un tabel de distribuție a frecvenței, care poate fi construit din parcele de tulpină și frunze sau direct din date.frecvența cumulativă se calculează prin adăugarea fiecărei frecvențe dintr-un tabel de distribuție a frecvenței la suma predecesorilor săi., Ultima valoare va fi întotdeauna egală cu totalul pentru toate observațiile, deoarece toate frecvențele vor fi deja adăugate la totalul anterior.

variabile Discrete sau continue

variabilele din orice calcul pot fi caracterizate prin valoarea atribuită acestora. O variabilă discretă constă din categorii separate, indivizibile. Nu pot exista valori între o variabilă și vecinul său. De exemplu, dacă observați o prezență la clasă înregistrată de la o zi la alta, puteți descoperi că clasa are 29 de elevi într-o zi și 30 de elevi în alta., Cu toate acestea, este imposibil ca participarea studenților să fie între 29 și 30 de ani. (Pur și simplu nu există loc pentru a observa valori între aceste două valori, deoarece nu există nicio modalitate de a avea 29 de studenți și jumătate.)

nu toate variabilele sunt caracterizate ca discrete. Unele variabile (cum ar fi timpul, înălțimea și greutatea) nu se limitează la un set fix de categorii indivizibile. Aceste variabile sunt numite variabile continue și sunt divizibile într-un număr infinit de valori posibile. De exemplu, timpul poate fi măsurat în părți fracționare de ore, minute, secunde și milisecunde., Deci, în loc să termine o cursă în 11 sau 12 minute, un jockey și calul său pot trece linia de sosire la 11 minute și 43 de secunde.este esențial să cunoaștem diferența dintre cele două tipuri de variabile pentru a calcula corect frecvența lor cumulativă.

Exemplul 1-variabile Discrete

numărul total de alpiniști din Lake Louise, Alberta a fost înregistrat pe o perioadă de 30 de zile. Rezultatele sunt următoarele:

31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56, 4, 54, 39, 52, 35, 51, 63, 42.,e variabile discrete la:

• a înființat o tulpină și frunze de teren, (a se vedea secțiunea privind stem și frunze de parcele) cu coloane suplimentare etichetate Frecvență, Valoare superioară și frecvența Cumulată
• da seama de frecvența de observații pentru fiecare stem
• găsi valoarea superioară pentru fiecare stem
• se calculează frecvența cumulată prin adăugarea de numere în Frecvență coloana
• a înregistra toate rezultatele din teren

se Trasează un grafic folosind axa y (sau linie verticală) pentru frecvența cumulată și axa x (sau linie orizontală) pentru numărul de persoane alpinism.,

răspunsuri:

1. numărul de alpiniști variază de la 4 la 65. Pentru a produce un complot stem și frunze, datele sunt cel mai bine grupate în intervale de clasă de 10.

   fiecare interval poate fi localizat în coloana Stem. Numerele din această coloană reprezintă primul număr din intervalul de clasă. (De exemplu, tulpina 0 reprezintă intervalul 0-9, tulpina 1 reprezintă intervalul 10-19 și așa mai departe.)

   coloana frunze listează numărul de observații care se află în fiecare interval de clasă., De exemplu, în Stem 2 (intervalul 20-29), cele trei observații, 23, 24 și 26, sunt reprezentate ca 3, 4 și 6.

   coloana frecvență listează numărul de observații găsite într-un interval de clasă. De exemplu, în tulpina 5, au fost găsite nouă frunze (sau observații); în tulpina 1, există doar două.

   utilizați coloana de frecvență pentru a calcula frecvența cumulativă.

   • mai întâi, adăugați numărul din coloana de frecvență la predecesorul său. De exemplu, în Stem 0, avem doar o singură observație și nici predecesorii. Frecvența cumulativă este una.,
     1 + 0 = 1
   • Cu toate acestea, în Stem 1, Există două observații. Adăugați aceste două la frecvența cumulativă anterioară (una), iar rezultatul este de trei.
     1 + 2 = 3
   • în Stem 2, Există trei observații. Adăugați aceste trei la frecvența cumulativă anterioară (trei), iar totalul (șase) este frecvența cumulativă pentru Stem 2.
     3 + 3 = 6
   • continuați aceste calcule până când ați adăugat toate numerele din coloana de frecvență.
   • înregistrați rezultatele în coloana de frecvență cumulativă.,

   coloana valoare superioară listează observația (variabila) cu cea mai mare valoare în fiecare dintre intervalele de clasă. De exemplu, în Stem 1, cele două observații 8 și 9 reprezintă variabilele 18 și 19. Valoarea superioară a acestor două variabile este 19.

   Tabelul 1.,>8 9

   2	19	1 + 2 = 3
   2	3 4 6	3	26	3 + 3 = 6
   3	1 5 5 7 9	5	39	6 + 5 = 11
   4	0 1 2 3 5 9	6	49	11 + 6 = 17
   5	0 1 1 2 4 4 5 6 7	9	57	17 + 9 = 26
   6	0 2 3 5	4	65	26 + 4 = 30

2. Since these variables are discrete, use the upper values in plotting the graph., Trasați punctele pentru a forma o curbă continuă numită ogive.

   etichetați întotdeauna graficul cu frecvența cumulativă-corespunzătoare numărului de observații efectuate-pe axa verticală.,bel axa orizontală cu alte variabile (în acest caz, totalul rock climber contează) așa cum se arată mai jos:

   

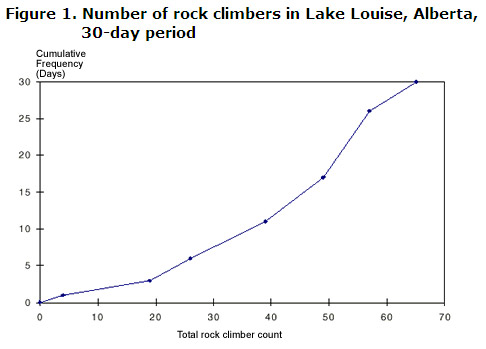
următoarele informații pot fi obținute fie din grafic sau tabel:

• pe 11 din cele 30 de zile, 39 de persoane sau mai puține urcat pe stânci în apropiere Lake Louise
• pe 13 din cele 30 de zile, 50 sau mai multe persoane urcat pe stânci în apropiere Lake Louise

atunci Când o variabilă continuă este folosit, atât calcularea frecvenței cumulative și trasarea graficului necesită o abordare ușor diferită de cea utilizată pentru variabile discrete.,

Exemplul 2 – variabile Continue

Pentru 25 de zile, grosimea stratului de zăpadă la Whistler Mountain, B. C. a fost măsurată (de la cel mai apropiat centimetru) și înregistrate după cum urmează:

242, 228, 217, 209, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257.,

1. Utilizarea continuă a variabilelor de mai sus pentru:
   • setați o frecvență de distribuție de masă
   • găsi frecvența pentru fiecare clasa interval
   • a localiza punctul final pentru fiecare clasa interval
   • se calculează frecvența cumulată prin adăugarea de numere în Frecvență coloana
   • a înregistra toate rezultatele în tabel
2. Folosi informațiile adunate de la frecvența de distribuție de masă să complot o frecvență cumulativă grafic.

răspunsuri:

1. măsurătorile adâncimii zăpezii variază de la 209 cm la 266 cm., Pentru a produce tabelul de distribuție a frecvenței, datele sunt cel mai bine grupate în intervale de clasă de 10 cm fiecare.

   în coloana de adâncime a zăpezii, este listat fiecare interval de clasă de 10 cm de la 200 cm la 270 cm.coloana de frecvență înregistrează numărul de observații care se încadrează într-un anumit interval. Această coloană reprezintă observațiile din coloana Tally, numai în formă numerică.,

   coloana punct final funcționează la fel ca coloana valoare superioară a exercițiului 1, cu excepția faptului că punctul final este cel mai mare număr din interval, indiferent de valoarea reală a fiecărei observații. De exemplu, în intervalul de clasă 210-220, valoarea reală a celor două observații este 217 și 219. Dar, în loc să utilizați 219, se utilizează punctul final al 220.

   coloana de frecvență cumulativă listează totalul fiecărei frecvențe adăugate predecesorului său.

   Tabelul 2. Adâncimea zăpezii măsurată la Whistler Mountain, B. C.,e2cd5a9″>

   5	240	11
   240 to < 250		7	250	18
   250 to < 260		5	260	23
   260 to < 270		2	270	25

2. Because the variable is continuous, the endpoints of each class interval are used in plotting the graph., Punctele reprezentate grafic sunt unite pentru a forma un ogive.

   rețineți că frecvența cumulativă (numărul de observații efectuate) este marcată pe axa verticală y și orice altă variabilă (adâncimea zăpezii) este marcată pe axa orizontală X, așa cum se arată în Figura 2.,

   

următoarele informații pot fi obținute fie din grafic sau tabel:

• nici unul dintre cei 25 de zile a nins adâncime mai mică decât 200 cm
• una dintre cele 25 de zile de zăpadă a avut adâncime de mai puțin de 210 cm
• două dintre cele 25 de zile de zăpadă a avut adâncimea de 260 cm sau mai mult

Alte frecvența cumulată calcule

un Alt calcul, care pot fi obținute folosind o frecvență de distribuție de masă este frecvența relativă de distribuție. Această metodă este definită ca procentul de observații care se încadrează în fiecare interval de clasă., Frecvența cumulativă relativă poate fi găsită prin împărțirea frecvenței fiecărui interval la numărul total de observații. (Pentru mai multe informații, consultați distribuția frecvenței în capitolul intitulat organizarea datelor.un tabel de distribuție a frecvenței poate fi, de asemenea, utilizat pentru a calcula procentul cumulativ. Această metodă de distribuție a frecvenței ne dă procentul frecvenței cumulative, spre deosebire de procentul frecvenței doar.