The colors of the body of the table illustrate the number of ways to throw each total., A probabilidade de atirar qualquer total dado é o número de maneiras de atirar esse total dividido pelo número total de combinações (36). Na tabela seguinte, o número específico de maneiras de lançar cada total e a probabilidade de atirar esse total é mostrada.

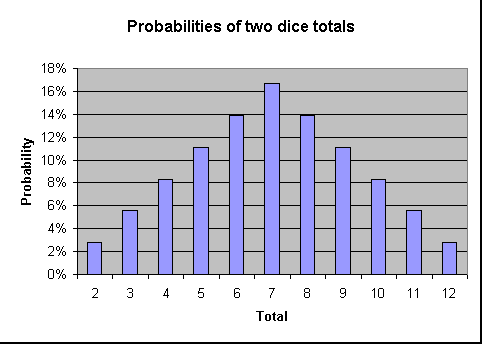
o seguinte mostra a probabilidade de lançar cada total num formato gráfico. Como o gráfico mostra quanto mais perto o total é de 7, Maior é a probabilidade de ser lançado.,

o exemplo de Aposta de campo

Agora que compreendemos a probabilidade de lançar cada total, podemos aplicar esta informação aos jogos de dados nos casinos para calcular a borda da casa. Por exemplo, considere a aposta de campo em dados. Esta aposta paga 1: 1 (dinheiro par) Se o próximo lance é um 3, 4, 9, 10, ou 11, 2:1 (dobrar a aposta) sobre o 2, e 3:1 (triplicar a aposta) sobre o 12. Note que há 7 totais que ganham e apenas 4 que perdem o que pode causar alguém que não sabia melhor para pensar que era uma boa aposta.,

o retorno do jogador pode ser definido como a soma dos produtos da probabilidade de cada evento e o retorno líquido desse evento. A tabela seguinte mostra cada total possível, o retorno líquido, a probabilidade de atirar esse total, e o retorno médio. O retorno médio é o produto do retorno líquido e da probabilidade. O retorno do jogador é a soma dos retornos médios.

a última linha mostra o retorno do jogador a ser -.0278, em outras palavras para cada aposta de $1 o jogador pode esperar perder 2,78 centavos., A perda do jogador é o ganho da casa, então a borda da casa é o produto de -1 e o retorno do jogador, neste caso 0,0278 ou 2,78%.

para as probabilidades na soma de mais de dois dados, por favor veja as minhas probabilidades para a secção de 1 a 25 dados.

escrito por: Michael Shackleford