- Histórico
- Magnitude Aparente m
- a Magnitude Absoluta, M
- Encontrar a Distância das Estrelas – Distância Módulo de elasticidade
- Magnitude/Cálculos de Distância
- Nomenclatura & Identificação de Estrelas
Estudo o campo de estrelas fotografia mostrado abaixo. Ele mostra uma região do céu em torno da constelação Crux, comumente chamada de Cruz do Sul. Mova o seu cursor através da foto para identificar algumas estrelas.qual é a estrela mais brilhante?,

uma fotografia como esta mostra estrelas brilhantes como discos maiores do que Estrelas mais fracas., Isso significa que estas estrelas são fisicamente maiores do que as estrelas mais fracas na foto? Lembre-se, na seção sobre astrometria aprendemos que todas as estrelas, além do nosso Sol, estão tão distantes que elas são efetivamente fontes pontuais. Por que, então, alguns parecem mais brilhantes (para os nossos olhos) ou maiores (em fotografias) do que outros? O que, na verdade, é brilho e como podemos medi-lo? As respostas a estas perguntas são o foco desta seção.,
antecedentes históricos

o conceito de medir e comparar o brilho das estrelas pode ser rastreado até o astrônomo e matemático grego Hiparco (190 – 120 a. C.). Um dos maiores astrônomos da antiguidade, ele é creditado por produzir um catálogo de 850 estrelas com posições e luminosidade comparativas., Em seu sistema, as estrelas mais brilhantes receberam uma magnitude de 1, a seguinte magnitude mais brilhante de 2 e assim por diante para as estrelas mais fracas, apenas visíveis a olho nu, que eram de magnitude 6. Esta escala de seis pontos pode ser considerada como uma classificação, Estrelas de primeira categoria, as mais brilhantes, eram de primeira magnitude e Estrelas de baixa velocidade dim eram de sexta magnitude.a descoberta de estrelas mais fracas com telescópios no início de 1600 exigiu que a escala fosse estendida para além da magnitude 6., O desenvolvimento de fotômetros visuais, instrumentos para medir intensidades estelares, no século XIX por John Herschel e outros, levou à necessidade de astrônomos adotarem um padrão internacional. O fato de que os olhos detectam diferenças de intensidade logaritmicamente em vez de linearmente foi descoberto na década de 1830. em 1856 Norman Pogson propôs que uma estrela de magnitude 1 era 100 × mais brilhante do que uma estrela de magnitude 6. Uma diferença de uma magnitude foi, portanto, igual a 5√100 = 2.512 vezes em brilho.,a magnitude aparente de uma estrela é a magnitude aparente observada por um observador na Terra. um objeto muito brilhante, como o sol ou a lua, pode ter uma magnitude aparente negativa. Apesar de Hiparco ter originalmente atribuído às estrelas mais brilhantes uma magnitude de 1 mais cuidadosa comparação mostra que a estrela mais brilhante no céu noturno, Sirius Ou α Canis Majoris (CMa) tem realmente uma magnitude aparente de m = -1,44. Com a recalibração dos valores originais de Hiparco, a estrela brilhante Vega é agora definida como tendo uma magnitude aparente de 0,0.,
Após a descoberta telescópica de estrelas fracas no início de 1600, a escala de magnitude também teve de ser estendida a objetos mais fracos do que a magnitude 6. A tabela abaixo mostra a gama de magnitudes aparentes para objetos celestes.
| Objeto | Aparente Magnitude |
|---|---|
| Sol |
-26.5
|
| Lua Cheia |
-12.5
|
| Vênus |
-4.,3
|
| Mars or Jupiter |
-2
|
| Sirius (α CMa) |
-1.44
|
| Vega (α Lyr) |
0.0
|
| Alnair (α Gru) |
1.73
|
| Naked-eye limit |
6.5
|
| Binocular limit |
10
|
| Proxima Cen |
11.,09
|
| Visual limit through 20 cm telescope |
14
|
| QSO at redshift z = 2 |
≈ 20
|
| Cepheid in galaxy M100 observed with HST |
26
|
| Galaxy at z = 6 observed with Gemini 8.1 m telescope |
28
|
| Limit for James Webb Space Telescope |
≥ 30
|
If a star of magnitude 1 is 2.,512 × mais brilhante que uma estrela de magnitude 2 e 100 &vezes mais brilhante que uma estrela de sexta magnitude quanto mais brilhante é do que uma estrela de magnitude 3? Tens de ter cuidado. Não é simplesmente 2 × 2.512 diferente. Você precisa lembrar que uma diferença de uma magnitude é igual a 5√100 = 2.512. Uma diferença de 2 magnitudes portanto = 2.5122 = 6.31 × diferença no brilho.
dois objetos de diferentes magnitudes, portanto, variam em brilho em 2.512 elevado ao poder da diferença de magnitude de TI., Se podemos escrever isso como uma equação, a taxa de brilho ou intensidade, IA/IB entre dois objetos, A e B, com magnitudes mA e mB é dada pela equação a seguir:
Vamos dar uma olhada em um exemplo.exemplo 1: comparar duas estrelas.quanto mais brilhante é Alnair, magnitude aparente de + 1,73 que Proxima Cen com uma magnitude de 11,09?
Usando a equação 4.1, temos:
assim, substituindo em:
Exemplo 2: Quanto mais brilhante é o Sol do que a Lua cheia?para isso, lembramos da tabela acima que o Sol tem uma magnitude aparente de -26,5 e a lua cheia, – 12,5.
Então, usando a equação 4.1, nós obtemos:
a substituir dá-nos a:
é importante lembrar que a magnitude é simplesmente um número, não tem quaisquer unidades. O símbolo de magnitude aparente é um caso menor m; você deve deixar isso claro em qualquer problema.
Magnitude absoluta, M
o que o fato de Sirius ter uma magnitude aparente de -1.44 e Betelgeuse uma magnitude aparente de 0,45 nos diz sobre estas duas estrelas? Outra maneira de pensar sobre isso é perguntar Por que Sirius é a estrela mais brilhante no céu noturno?, Uma estrela pode parecer brilhante, por duas razões principais:
- pode ser intrinsecamente luminoso, que poderá ser um poderoso emissor de radiação eletromagnética, ou
- pode ser muito perto de nós, ou ambos.
a magnitude aparente de uma estrela depende em parte da sua distância de nós. Na verdade Sirius parece mais brilhante do que Betelgeuse precisamente porque Sirius está muito perto de nós, a apenas 2,6 pc de distância, enquanto Betelgeuse está a cerca de 160 pc de distância., A percepção de que as estrelas não têm todas a mesma luminosidade significava que a magnitude aparente por si só não era suficiente para comparar as estrelas. Um novo sistema que permitiria aos astrônomos comparar diretamente as estrelas foi desenvolvido. Este sistema é chamado a magnitude absoluta, M.
A magnitude absoluta, M, de uma estrela é a magnitude que a estrela teria se estivesse a uma distância de 10 parsecs de nós. Uma distância de 10 pc é puramente arbitrária, mas agora internacionalmente acordada por astrônomos., A escala de magnitude absoluta é a mesma que a da magnitude aparente, que é uma diferença de 1 magnitude = 2.512 vezes de diferença no brilho. Esta escala logarítmica também é aberta e sem unidade. Mais uma vez, quanto menor ou mais negativo o valor de M, Mais brilhante a estrela é. Magnitude absoluta é uma forma conveniente de expressar a luminosidade de uma estrela. Uma vez que a magnitude absoluta de uma estrela é conhecida Você também pode compará-la com outras estrelas. Betelgeuse, M = -5.6 é intrinsecamente mais luminosa do que Sirius com um m = 1.41.o nosso Sol tem uma magnitude visual absoluta de 4,8.,como se pode lembrar da secção sobre astrometria, a maioria das estrelas está muito distante para que a sua paralaxe seja medida directamente. No entanto, se você sabe tanto as magnitudes aparente e absoluta para uma estrela você pode determinar a sua distância. Vamos olhar novamente para Sirius e Betelgeuse mais outra estrela chamada GJ 75.a que distância está o GJ 75? É uma estrela incomum na medida em que suas magnitudes aparentes e absolutas são as mesmas. Por quê? A razão é que está realmente 10 parsecs distante de nós, assim que por definição suas duas magnitudes devem ser as mesmas.,e o Sirius? Sua magnitude aparente é igual a 2.58. Isto significa que é mais perto de 10 parsecs para nós. A magnitude aparente de Betelgeuse é maior (portanto mais fraca) do que a sua magnitude absoluta, de modo que pareceria ainda mais brilhante no céu noturno se estivesse apenas a 10 parsecs de distância.
os astrónomos usam a diferença entre a magnitude aparente e a magnitude absoluta, o módulo de distância, como uma forma de determinar a distância a uma estrela. o módulo de elasticidade é negativo para Estrelas mais próximas do que 10 parsecs.,o módulo de distância é positivo para Estrelas mais afastadas do que 10 parsecs.
cálculos de Magnitude/distância
o módulo de elasticidade pode ser usado para determinar a distância a uma estrela usando a equação:
onde d está em parsecs. Note que se d = 10 pc então m E M são os mesmos. (Uma derivação formal desta equação é dada na página seguinte sobre luminosidade)., A folha de Fórmula syllabus NSW HSC fornece a equação como:
mas esta é simplesmente uma reformulação da equação 4.2. Você deve estar confortável em resolver esta equação dada qualquer duas das três variáveis. Deixe-nos saber como você pode resolver alguns exemplos.
exemplo 3: dado m E d, é necessário encontrar M.
β Crucis (ou Mimosa) tem uma magnitude aparente de 1,25 e está a 108 parsecs de distância. Qual é a sua magnitude absoluta?
Usando a equação 4.3, temos:
então, β-Sacra tem uma magnitude absoluta de -3.92
Nota: este cálculo tem mostrado cheia de trabalho, de modo que cada passo é explícito. (Lembre-se em resolver equações de magnitude log refere-se a logaritmos de base 10 e não logaritmos naturais ou ln.)
Exemplo 4: Dado m e M, encontrar d.
Betelgeuse tem uma magnitude aparente de 0,45 e uma magnitude absoluta de -5.14. A que distância fica?este problema requer que reescrevamos a equação 4.2 para nos dar d como o desconhecido., Isso é mostrado abaixo:
o que pode ser escrito como:
agora, substituindo em:
então, Betelgeuse é de cerca de 130 pc distante.
Mais uma vez, este exemplo mostra o trabalho completo, enquanto na realidade você não pode mostrar cada passo., É importante, no entanto, que você defina seu trabalho para tais problemas claramente para que você possa verificar a sua manipulação algébrica e suas substituições. Trabalhar com logs e índices pode ser complicado para garantir que você sabe como fazer isso em sua calculadora.
Exemplo 5: Dado M e d, encontrar m.
Na prática, este tipo de problema é menos realista de objetos reais como normalmente podemos medir suas magnitudes aparentes diretamente no entanto, pode ser que desejamos calcular a magnitude aparente de uma classe ou tipo de objeto pode ter dado a outros parâmetros. Novamente, começando pela equação 4.,3 vamos determinar o quão brilhante uma supergigante como Deneb com uma magnitude absoluta de -8.73 apareceria se estivesse a 230 parsecs de distância.
então, substituindo em:
então, Deneb teria uma magnitude aparente de -1.89. Isso faria com que fosse mais brilhante em nosso céu noturno do que Sirius (m = -1.44)., Na realidade Deneb é cerca de 990 pc distante, embora este valor tem uma grande incerteza.
exemplo 6: e se o d não for dado mas o paralaxe, o p for dado?
Isto é realmente muito direto para a frente. Lembre-se da seção sobre astrometria que existe uma relação direta entre Distância e paralaxe.
portanto, basta inserir isto na equação 4.2 ou 4.3.
Naming & Identifying Stars
Let us know revisit that photo of Crux and the Pointers from the top of this page., A foto abaixo mostra a mesma região com as estrelas proeminentes marcadas. Eles também têm suas magnitudes aparentes mostradas. Crux é uma constelação do hemisfério celestial, uma das 88 regiões em que a esfera celeste foi dividida e acordada internacionalmente por astrônomos. Crux é na verdade a menor das constelações e é facilmente identificado nos céus do Sul. As estrelas próximas proeminentes comumente chamadas de ponteiros são na verdade parte de uma grande constelação chamada Centaurus.

Agora você pode perceber que as estrelas são nomeados com letras do alfabeto grego; α, β, γ δ e ε (alfa, beta, gama, delta, epsilon, sendo o primeiro de cinco), seguido pelo padrão de abreviação de três letras para cada constelação (Cru para Crucis ou Crux e o Cen para Centaurus). Se você olhar de perto para as magnitudes aparentes para as cinco estrelas nomeadas em Crux você verá que a estrela mais brilhante é rotulado α, o próximo β e assim por diante., Este sistema é chamado de Sistema Bayer, em homenagem a Johann Bayer, que o introduziu em 1603. A estrela mais brilhante de uma constelação recebe a letra α, o próximo β e assim por diante. Uma exceção a esta regra é &alpha Orionis ou Betelgeuse. Na verdade, é mais fraco do que β Ori, Rigel por uma pequena quantidade. Este é um caso histórico interessante resolvido pela constatação de que Betelgeuse diminuiu ligeiramente no brilho desde que foi nomeado sob o sistema Bayer.,um ponto a lembrar sobre constelações é que as estrelas dentro de uma constelação não são normalmente associadas fisicamente umas com as outras, ao contrário das estrelas em aglomerados. O fato de aparecerem juntos é puramente um efeito de alinhamento ao longo da linha de visão. Na verdade, as estrelas na região acima estão amplamente separadas em distância de nós, como mostrado na imagem seguinte.
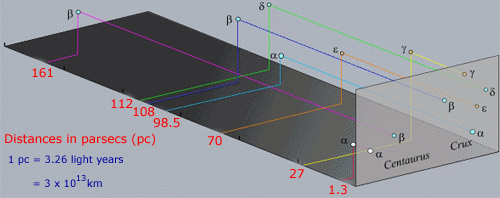
algumas das estrelas brilhantes Como α Cen também têm o seu próprio nome específico. Sirius (α Sco) é um desses exemplos, enquanto α Cen é também chamado Rigel Kentaurus. Muitos nomes de estrelas são de origem Árabe da época em que os registros gregos foram preservados e desenvolvidos por astrônomos islâmicos. O problema com o sistema Bayer de nomear estrelas é que existem apenas 24 letras no alfabeto grego, mas há muito mais estrelas do que a de cada constelação. a maioria das Estrelas, de facto, não tem um nome específico nem classificação Bayer., Hoje em dia os astrônomos compilaram vastos catálogos de estrelas, algumas com mais de 10 milhões de objetos, então a maioria das estrelas só tem um número de catálogo. As estrelas podem ter muito mais do que um nome de identificação ou número de catálogo, dependendo do número de catálogos em que estão. A estrela variável δ Cep, por exemplo, também é conhecida como HIP 110991, SAO 34508, ou qualquer outro de mais de 30 identificadores! Muitos catálogos utilizam coordenadas celestes como ascensão reta e declinação para identificar objetos. Assim, δ Cep é conhecido como IRAS 22273+5809, CCDM J22292+5825A e AAVSO 2225+57., As ligeiras variações de RA e dec para os catálogos surgem devido ao movimento próprio das estrelas e à precessão do quadro de referência.