The colors of the body of the table illustrate the number of ways to throw each total., Prawdopodobieństwo wyrzucenia danej sumy jest liczbą sposobów rzucenia tej sumy podzieloną przez całkowitą liczbę kombinacji (36). W poniższej tabeli pokazano określoną liczbę sposobów rzucania każdej sumy i prawdopodobieństwo rzucenia tej sumy.

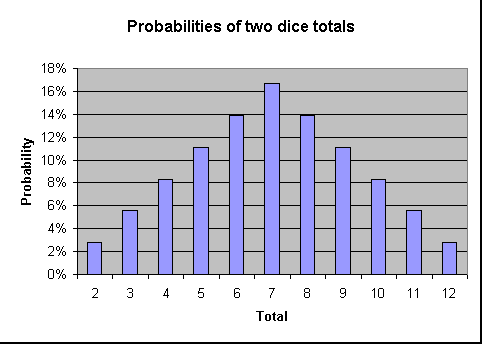
poniżej przedstawiono prawdopodobieństwo wyrzucenia każdej sumy w formacie wykresu. Jak pokazuje wykres im bliżej jest suma do 7, tym większe jest prawdopodobieństwo wyrzucenia.,

przykład zakładu w polu

teraz, gdy rozumiemy prawdopodobieństwo wyrzucenia każdej sumy, możemy zastosować te informacje do gier w kościach w kasynach, aby obliczyć przewagę kasyna. Na przykład rozważ zakład na pole w kościach. Ten zakład jest wypłacany 1: 1 (parzyste pieniądze), jeśli następny rzut to 3, 4, 9, 10 lub 11, 2:1 (podwójna stawka) na 2 i 3:1 (potrójna stawka) na 12. Zauważ, że jest 7 liczb, które wygrywają i tylko 4, które przegrywają, co może spowodować, że ktoś, kto nie wiedział lepiej, uzna to za dobry Hazard.,

zwrot gracza może być zdefiniowany jako suma iloczynów prawdopodobieństwa każdego zdarzenia i zwrotu netto tego zdarzenia. Poniższa tabela pokazuje każdą możliwą sumę, zwrot netto, prawdopodobieństwo wyrzucenia tej sumy i średni zwrot. Średni zysk jest iloczynem zysku netto i prawdopodobieństwa. Zwrot gracza jest sumą średnich zwrotów.

ostatni wiersz pokazuje powrót gracza do be -.0278, innymi słowy za każdy zakład $1 gracz może spodziewać się stracić 2.78 centów., Strata gracza jest zyskiem kasyna, więc przewaga kasyna jest iloczynem -1 i zwrotu gracza, w tym przypadku 0,0278 lub 2,78%.

dla prawdopodobieństwa w sumie więcej niż dwie kości proszę zobaczyć moje prawdopodobieństwa dla 1 do 25 kości sekcji.

autor: Michael Shackleford