Częstotliwość skumulowana

• przykład 1 – zmienne dyskretne
• przykład 2 – zmienne ciągłe
• inne obliczenia skumulowanej częstotliwości

skumulowana częstotliwość jest używana do określenia liczby obserwacji, które leżą powyżej (lub poniżej) określonej wartości w zbiorze danych. Skumulowana częstotliwość jest obliczana przy użyciu tabeli rozkładu częstotliwości, która może być zbudowana z działek łodygi i liści lub bezpośrednio z danych.

częstotliwość skumulowana jest obliczana przez dodanie każdej częstotliwości z tabeli rozkładu częstotliwości do sumy jej poprzedników., Ostatnia wartość będzie zawsze równa sumie dla wszystkich obserwacji, ponieważ wszystkie częstotliwości zostaną już dodane do poprzedniej sumy.

zmienne dyskretne lub ciągłe

zmienne w dowolnych obliczeniach można scharakteryzować przypisaną im wartością. Zmienna Dyskretna składa się z oddzielnych, niepodzielnych kategorii. Pomiędzy zmienną a jej sąsiadem nie mogą istnieć żadne wartości. Na przykład, jeśli obserwujesz obecność w klasie zarejestrowaną z dnia na dzień, możesz odkryć, że klasa ma 29 uczniów w jednym dniu i 30 uczniów w innym., Jednak nie jest możliwe, aby frekwencja uczniów wynosiła między 29 a 30. (Po prostu nie ma miejsca na obserwowanie jakichkolwiek wartości między tymi dwoma wartościami, ponieważ nie ma możliwości posiadania 29 i pół uczniów.)

nie wszystkie zmienne są scharakteryzowane jako dyskretne. Niektóre zmienne (takie jak czas, wzrost i waga) nie są ograniczone do ustalonego zbioru niepodzielnych kategorii. Zmienne te nazywane są zmiennymi ciągłymi i są podzielne na nieskończoną liczbę możliwych wartości. Na przykład czas można mierzyć w ułamkowych częściach Godzin, Minut, Sekund i milisekund., Tak więc, zamiast ukończyć wyścig w 11 lub 12 minut, dżokej i jego koń mogą przekroczyć linię mety w 11 minut i 43 sekundy.

ważne jest, aby znać różnicę między dwoma typami zmiennych, aby prawidłowo obliczyć ich skumulowaną częstotliwość.

przykład 1 – zmienne dyskretne

całkowita liczba wspinaczy skalnych w Lake Louise w Albercie została zarejestrowana w okresie 30 dni. Wyniki są następujące:

31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56, 4, 54, 39, 52, 35, 51, 63, 42.,e zmienne dyskretne do:

• Ustaw Wykres łodygi i liścia (patrz sekcja na działkach łodygi i liścia) z dodatkowymi kolumnami oznaczonymi częstotliwością, górną wartością i częstotliwością kumulacyjną
• Oblicz częstotliwość kumulacyjną dla każdego łodygi
• Oblicz częstotliwość kumulacyjną przez dodanie liczb w kolumnie częstotliwości
• zapisz wszystkie wyniki na wykresie

Wykreśl Wykres za pomocą osi Y (lub linia pionowa) dla częstotliwości kumulacyjnej i osi X (lub linia pozioma) dla liczby osób wspinających się na skały.,

odpowiedzi:

1. liczba wspinaczy skalnych waha się od 4 do 65. Aby uzyskać Wykres łodygi i liści, dane najlepiej pogrupować w odstępach klasowych po 10.

   każdy interwał może być umieszczony w kolumnie macierzystej. Liczby w tej kolumnie reprezentują pierwszą liczbę w przedziale klasowym. (Na przykład trzon 0 reprezentuje interwał 0-9, trzon 1 reprezentuje interwał 10-19 itd.)

   w kolumnie Leaf podano liczbę obserwacji, które znajdują się w każdym przedziale klasowym., Na przykład w łodydze 2 (przedział 20-29) trzy obserwacje, 23, 24 i 26, są reprezentowane jako 3, 4 i 6.

   kolumna Frequency pokazuje liczbę obserwacji znalezionych w przedziale klasowym. Na przykład w łodydze 5 znaleziono dziewięć liści (lub obserwacje); w łodydze 1 są tylko dwa.

   użyj kolumny częstotliwości, aby obliczyć łączną częstotliwość.

   • najpierw dodaj liczbę z kolumny Frequency do jej poprzednika. Na przykład w Stem 0 mamy tylko jedną obserwację i żadnych poprzedników. Łączna częstotliwość wynosi 1.,
     1 + 0 = 1
   • jednak w Stem 1 istnieją dwie obserwacje. Dodaj te dwa do poprzedniej skumulowanej częstotliwości (jednej), a wynik będzie trzy.
     1 + 2 = 3
   • w Stem 2 istnieją trzy obserwacje. Dodaj te trzy do poprzedniej częstotliwości skumulowanej (trzy), a całkowita (sześć) to skumulowana częstotliwość dla Stem 2.
     3 + 3 = 6
   • Kontynuuj te obliczenia, dopóki nie dodasz wszystkich liczb w kolumnie Częstotliwość.
   • Zapisz wyniki w kolumnie częstotliwości kumulacyjnej.,

   górna kolumna wartości wyświetla obserwację (zmienną) o najwyższej wartości w każdym z przedziałów klasy. Na przykład, w Stem 1, dwie obserwacje 8 i 9 reprezentują zmienne 18 i 19. Górna wartość tych dwóch zmiennych to 19.

   Tabela 1.,>8 9

   2	19	1 + 2 = 3
   2	3 4 6	3	26	3 + 3 = 6
   3	1 5 5 7 9	5	39	6 + 5 = 11
   4	0 1 2 3 5 9	6	49	11 + 6 = 17
   5	0 1 1 2 4 4 5 6 7	9	57	17 + 9 = 26
   6	0 2 3 5	4	65	26 + 4 = 30

2. Since these variables are discrete, use the upper values in plotting the graph., Wykreśl punkty, aby utworzyć ciągłą krzywą zwaną ostrością.

   zawsze na osi pionowej oznaczamy Wykres częstotliwością skumulowaną—odpowiadającą liczbie wykonanych obserwacji.,poniżej znajduje się oś pozioma z drugą zmienną (w tym przypadku liczy się całkowity wspinacz), jak pokazano poniżej:

   

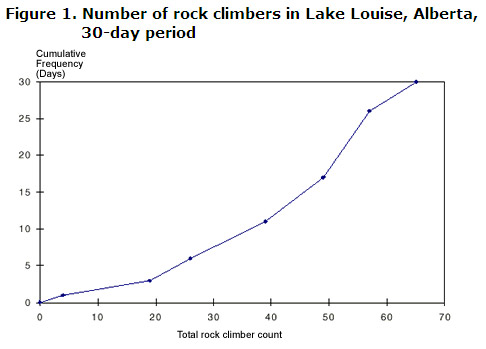
poniższe informacje można uzyskać z wykresu lub tabeli:

• w 11 z 30 dni 39 osób lub mniej wspinało się po skałach wokół Lake Louise
• w 13 z 30 dni, 50 lub więcej osób wspinało się po skałach wokół Lake Louise

gdy używana jest zmienna ciągła, zarówno obliczanie częstotliwości skumulowanej, jak i wykreślanie wykresu wymagają nieco innego podejścia niż stosowane dla zmiennej dyskretnej.,

przykład 2-zmienne ciągłe

przez 25 dni głębokość śniegu na górze Whistler w B. C. była mierzona (z dokładnością do centymetra) i zapisywana w następujący sposób:

242, 228, 217, 209, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257.,

1. użyj powyższych zmiennych ciągłych, aby:
   • Ustaw tabelę rozkładu częstotliwości
   • znajdź częstotliwość dla każdego przedziału klas
   • znajdź punkt końcowy dla każdego przedziału klas
   • Oblicz skumulowaną częstotliwość przez dodanie liczb w kolumnie częstotliwości
   • zapisz wszystkie wyniki w tabeli
2. Użyj informacji zebranych z tabeli rozkładu częstotliwości do wykreślenia skumulowanego wykresu częstotliwości.

odpowiedzi:

1. pomiary głębokości śniegu wahają się od 209 cm do 266 cm., Aby stworzyć tabelę rozkładu częstotliwości, dane najlepiej pogrupować w odstępach klasowych po 10 cm każdy.

   w kolumnie głębokość śniegu podano każdy przedział klasowy 10 cm od 200 cm do 270 cm.

   kolumna częstotliwości rejestruje liczbę obserwacji, które mieszczą się w określonym przedziale. Ta kolumna przedstawia obserwacje w kolumnie Tally, tylko w postaci liczbowej.,

   kolumna punktu końcowego działa podobnie jak górna kolumna wartości ćwiczenia 1, z tym wyjątkiem, że punkt końcowy jest najwyższą liczbą w przedziale, niezależnie od rzeczywistej wartości każdej obserwacji. Na przykład, w przedziale klasowym 210-220, rzeczywista wartość obu obserwacji wynosi 217 i 219. Ale zamiast używać 219, używany jest punkt końcowy 220.

   Kolumna Cumulative frequency zawiera sumę każdej częstotliwości dodanej do jej poprzednika.

   Tabela 2. Głębokość śniegu mierzona na górze Whistler, B. C.,e2cd5a9″>

   5	240	11
   240 to < 250		7	250	18
   250 to < 260		5	260	23
   260 to < 270		2	270	25

2. Because the variable is continuous, the endpoints of each class interval are used in plotting the graph., Wykreślone punkty są łączone w celu utworzenia ostrza.

   Należy pamiętać, że skumulowana częstotliwość (liczba wykonanych obserwacji) jest oznaczana na pionowej osi y, a każda inna zmienna (głębokość śniegu) jest oznaczana na poziomej osi x, jak pokazano na rysunku 2.,

   

poniższe informacje można uzyskać z wykresu lub tabeli:

• w żadnym z 25 dni śnieg miał głębokość mniejszą niż 200 cm
• w jednym z 25 dni śnieg miał głębokość mniejszą niż 210 cm
• w dwóch z 25 dni śnieg miał głębokość mniejszą niż 260 cm lub większą

inne skumulowane obliczenia częstotliwości

inne obliczenia, które można uzyskać za pomocą tabeli rozkładu częstotliwości, to względny rozkład częstotliwości. Metoda ta jest zdefiniowana jako procent obserwacji przypadający w każdym przedziale klasowym., Względną częstotliwość skumulowaną można znaleźć dzieląc częstotliwość każdego przedziału przez całkowitą liczbę obserwacji. (Aby uzyskać więcej informacji, zobacz rozkład częstotliwości w rozdziale zatytułowanym organizowanie danych.)

tabelę rozkładu częstotliwości można również wykorzystać do obliczenia skumulowanego procentu. Ta metoda rozkładu częstotliwości daje nam procent skumulowanej częstotliwości, w przeciwieństwie do procentu tylko częstotliwości.