• tło historyczne
• jasność pozorna, m
• absolutna, m
• Wyszukiwanie odległości od gwiazd – moduł odległości
• obliczenia jasności/odległości
• nazewnictwo & Identyfikacja gwiazd

zbadaj zdjęcie pola gwiazd pokazane poniżej. Pokazuje on obszar nieba wokół konstelacji Crux, potocznie nazywany Krzyżem południa. Przesuń kursor w poprzek zdjęcia, aby zidentyfikować niektóre gwiazdy.

która gwiazda jest najjaśniejsza?,

Jeśli odpowiedziałeś Alfa (α) Centauri, gwiazda w lewym dolnym rogu zdjęcia masz rację. Jak widać, taki fotograficzny obraz pokazuje o wiele więcej gwiazd, niż można zobaczyć własnym okiem. Niemniej jednak niektóre gwiazdy są bardziej widoczne niż inne. Wybierając α Centauri poczyniłeś pewne założenia. Co to było?

taka fotografia pokazuje jasne gwiazdy jako większe dyski od słabszych gwiazd., Czy to oznacza, że te gwiazdy są fizycznie większe od słabszych gwiazd na zdjęciu? Pamiętajcie, w dziale astrometrii dowiedzieliśmy się, że wszystkie gwiazdy inne niż nasze Słońce są tak odległe, że są faktycznie źródłami punktowymi. Dlaczego więc niektóre wydają się jaśniejsze (dla naszych oczu) lub większe (na zdjęciach) niż inne? Czym tak naprawdę jest jasność i jak możemy ją zmierzyć? Odpowiedzi na te pytania stanowią główny punkt tej sekcji.,

tło historyczne

pojęcie pomiaru i porównywania jasności gwiazd wywodzi się od greckiego astronoma i matematyka Hipparcha (190 – 120 p. n. e.). Jeden z największych astronomów starożytności, przypisuje mu się stworzenie katalogu 850 gwiazd z pozycjami i porównaniem jasności., W jego układzie najjaśniejsze gwiazdy miały jasność 1, kolejne najjaśniejsze 2 i tak dalej, najsłabszym gwiazdom, widocznym tylko dla oka, które miały jasność 6. Ta sześciopunktowa skala może być traktowana jako ranking, Gwiazdy pierwszorzędowe, najjaśniejsze, miały pierwszą wielkość, a najmniejsze-szóstą wielkość.

odkrycie słabszych gwiazd za pomocą teleskopów na początku XVI wieku wymagało rozszerzenia skali poza 6 magnitudo., Rozwój fotometrów wzrokowych, przyrządów do pomiaru intensywności gwiazd w XIX wieku przez Johna Herschela i innych skłonił astronomów do przyjęcia międzynarodowego standardu. Fakt, że oczy wykrywają różnice intensywności logarytmicznie, a nie liniowo, został odkryty w 1830 roku. w 1856 roku Norman Pogson zaproponował, że gwiazda o jasności 1 jest 100 × jaśniejsza od Gwiazdy o jasności 6. Różnica jednej wielkości była więc równa 5√100 = 2,512 razy jasności.,

jasność pozorna, m

jasność pozorna, m, gwiazdy jest wielkością widzianą przez obserwatora na Ziemi.

bardzo jasny obiekt, taki jak słońce lub księżyc, może mieć ujemną widoczną wielkość. Chociaż Hipparchus pierwotnie przypisał najjaśniejszym gwiazdom jasność 1 dokładniejsze porównanie pokazuje, że najjaśniejsza gwiazda na nocnym niebie, Syriusz lub α Canis Majoris (CMA), faktycznie ma jasność pozorną m = -1,44. Po ponownej kalibracji pierwotnych wartości Hipparchusa jasność gwiazdy Vega jest teraz zdefiniowana jako obserwowana wielkość 0,0.,

Po teleskopowym odkryciu słabych gwiazd we wczesnych latach XVI wieku skala jasności musiała zostać rozszerzona na obiekty słabsze niż jasność 6. Poniższa tabela przedstawia zakres widocznych wielkości dla obiektów niebieskich.

obiekt	pozorna wielkość
słońce	-26.5
pełnia księżyca	-12.5
Wenus	-4.,3
Mars or Jupiter	-2
Sirius (α CMa)	-1.44
Vega (α Lyr)	0.0
Alnair (α Gru)	1.73
Naked-eye limit	6.5
Binocular limit	10
Proxima Cen	11.,09
Visual limit through 20 cm telescope	14
QSO at redshift z = 2	≈ 20
Cepheid in galaxy M100 observed with HST	26
Galaxy at z = 6 observed with Gemini 8.1 m telescope	28
Limit for James Webb Space Telescope	≥ 30

If a star of magnitude 1 is 2.,512 × jaśniejsza od Gwiazdy o jasności 2 i 100 &razy jaśniejsza od Gwiazdy o jasności 6 magnitudo ile jest jaśniejsza od Gwiazdy o jasności 3? Musisz być ostrożny. Nie jest to po prostu 2 × 2.512 inny. Musisz pamiętać, że różnica jednej wielkości wynosi 5√100 = 2.512. Różnica 2 magnitudo = 2,5122 = 6,31 × różnica jasności.

dwa obiekty o różnej magnitudzie różnią się więc jasnością o 2,512 podniesioną do potęgi różnicy wielkości., Jeśli napiszemy to jako równanie, stosunek jasności lub intensywności, IA/IB między dwoma obiektami, A i B, o magnitudach mA i mB jest podany w następującym równaniu:

spójrzmy na przykład.

przykład 1: Porównanie dwóch gwiazdek.
o ile jaśniejsza jest Alnair o jasności obserwowanej + 1,73 niż Proxima Cen o jasności 11,09?
używając równania 4.1 mamy:

tak, zastępując w:

przykład 2: o ile jaśniejsze jest Słońce niż Księżyc w pełni?
w tym celu przypominamy z powyższej tabeli, że słońce ma jasność obserwowaną równą -26,5, a Księżyc w pełni – 12,5.

więc używając równania 4.1 otrzymujemy:

zastępowanie w daje nam:

ważne jest, aby pamiętać, że wielkość jest po prostu liczbą, nie ma żadnych jednostek. Symbolem pozornej wielkości jest mała litera m; musisz to wyjaśnić w każdym problemie.

wielkość absolutna, M

Co o tych dwóch gwiazdach mówi fakt, że Syriusz ma jasność pozorną -1,44, a Betelgeuse 0,45? Innym sposobem myślenia o tym jest pytanie, dlaczego Syriusz jest najjaśniejszą gwiazdą na nocnym niebie?, Gwiazda może wydawać się jasna z dwóch głównych powodów:

1. może być świecąca wewnętrznie, to znaczy może być silnym emiterem promieniowania elektromagnetycznego, lub
2. może być bardzo blisko nas, lub oba te czynniki.

pozorna wielkość Gwiazdy zależy więc częściowo od jej odległości od nas. W rzeczywistości Syriusz wydaje się jaśniejszy niż Betelgeuse właśnie dlatego, że Syriusz jest bardzo blisko nas, tylko 2,6 pc od nas, podczas gdy Betelgeuse jest około 160 pc od nas., Uświadomienie sobie, że gwiazdy nie wszystkie mają taką samą jasność oznaczało, że sama jasność pozorna nie była wystarczająca do porównania gwiazd. Opracowano nowy system, który umożliwiłby astronomom bezpośrednie porównywanie gwiazd. Ten system nazywa się absolutną wielkością, M.

absolutna wielkość, m, gwiazdy jest wielkością, że gwiazda miałaby, gdyby była w odległości 10 parseków od nas. Odległość 10 pc jest czysto arbitralna, ale obecnie międzynarodowo uzgodniona przez astronomów., Skala jasności absolutnej jest taka sama jak dla jasności pozornej, czyli różnica 1 wielkości = 2,512 razy różnica jasności. Ta skala logarytmiczna jest również otwarta i jednostkowa. Im niższa lub bardziej ujemna wartość M, tym jaśniejsza jest gwiazda. Wielkość absolutna jest wygodnym sposobem wyrażania jasności gwiazdy. Gdy znana jest absolutna wielkość Gwiazdy, można ją również porównać z innymi gwiazdami. Betelgeuse, M = -5,6 jest z natury bardziej świecący niż Syriusz z M = 1,41.

nasze Słońce ma absolutną jasność wizualną 4,8.,

znajdowanie odległości do gwiazd – moduł odległości

jak można przypomnieć z sekcji astrometrii, większość gwiazd jest zbyt odległa, aby ich paralaksa była mierzona bezpośrednio. Niemniej jednak, jeśli znasz zarówno jasność pozorną, jak i absolutną Gwiazdy, możesz określić jej odległość. Spójrzmy jeszcze raz na Syriusza i Betelgeuse oraz kolejną gwiazdę o nazwie GJ 75.

jak daleko jest GJ 75? Jest to niezwykła gwiazda, ponieważ jej jasność pozorna i absolutna są takie same. Dlaczego? Powodem jest to, że w rzeczywistości jest odległa od nas o 10 parseków, więc z definicji jego dwie wielkości muszą być takie same.,

a co z Syriuszem? Jego wielkość pozorna jest mniejsza (a więc jaśniejsza) niż wielkość absolutna. Oznacza to, że jest bliżej niż 10 parseków do nas. Jasność obserwowana Betelgeuse ' a jest wyższa (a więc ciemniejsza) niż jej absolutna wielkość, więc wyglądałaby jeszcze jaśniej na nocnym niebie, gdyby była oddalona tylko o 10 parseków.

astronomowie używają różnicy między jasnością pozorną a absolutną, modułu odległości, jako sposobu określenia odległości do gwiazdy.

• moduł odległości = m – M.
• moduł odległości jest ujemny dla gwiazd bliższych niż 10 parseków.,
• moduł odległości jest dodatni dla gwiazd położonych dalej niż 10 parseków.
• wielkość modułu odległości określa rzeczywistą wartość odległości, tak że gwiazda o module odległości 1,5 znajduje się bliżej niż gwiazda o module odległości 8,7.

obliczenia jasności/odległości

moduł odległości może być użyty do określenia odległości do gwiazdy za pomocą równania:

gdzie d jest w parsekach. Zauważ, że jeśli d = 10 pc to m I M są takie same. (Formalne wyprowadzenie tego równania jest podane na następnej stronie o jasności)., Arkusz Formuły NSW HSC Syllabus zawiera równanie w postaci:

ale jest to po prostu przeróbka równania 4.2. Powinieneś być wygodny w rozwiązywaniu tego równania, biorąc pod uwagę dowolne dwie z trzech zmiennych. Daj nam znać zobacz, jak możesz rozwiązać kilka przykładów.

przykład 3: biorąc pod uwagę m I d, trzeba znaleźć M.
β Crucis (lub Mimosa) ma obserwowaną wielkość 1,25 i jest odległa o 108 parseków. Jaka jest jego absolutna wielkość?

używając równania 4.3 mamy:

tak więc β Crucis ma absolutną wielkość -3.92
zauważ, że obliczenia te wykazały pełne działanie, tak że każdy krok jest jednoznaczny. (Pamiętaj w rozwiązywaniu równań wielkości log odnosi się do logarytmów do bazy 10, a nie logarytmów naturalnych lub ln.)

przykład 4: biorąc pod uwagę m I m, znajdź d.
Betelgeuse ma obserwowaną wielkość 0,45 i absolutną wielkość -5,14. Jak daleko to jest?
ten problem wymaga przepisania równania 4.2, aby dać nam d jako Nieznane., To jest pokazane poniżej:

które można zapisać jako:

teraz zastępuje się w:

więc Betelgeuse jest około 130 pc odległe.

Ten przykład pokazuje pełną pracę, podczas gdy w rzeczywistości możesz nie pokazywać każdego kroku., Ważne jest jednak, aby jasno ustawić swoją pracę na takie problemy, abyś mógł sprawdzić swoją manipulację algebraiczną i substytucje. Praca z dziennikami i indeksami może być trudna, więc upewnij się, że wiesz, jak to zrobić na kalkulatorze.

przykład 5: biorąc pod uwagę M I d, znajdź m.
w praktyce tego typu problem jest mniej realistyczny dla rzeczywistych obiektów, ponieważ możemy normalnie mierzyć ich pozorną wielkość bezpośrednio, jednak może być tak, że chcemy obliczyć, jaką pozorną wielkość klasa lub typ obiektu mogły podać inne parametry. Ponownie, zaczynając od równania 4.,3 ustalmy, jak jasny byłby supergiant taki jak Deneb o absolutnej wielkości -8,73, gdyby był oddalony o 230 parseków.

więc zastępowanie w:

div>

Tak więc Deneb miałby jasność pozorną -1,89. To uczyniłoby go jaśniejszym na naszym nocnym niebie niż Syriusz (m = -1,44)., W rzeczywistości Deneb jest odległy o około 990 pc, chociaż wartość ta ma dużą niepewność.

przykład 6: co jeśli nie podano d, ale podano paralaksę, P?
To jest właściwie bardzo proste. Przypomnijmy z sekcji astrometrii, że istnieje bezpośredni związek między odległością a paralaksą.

więc wystarczy wstawić to do równania 4.2 lub 4.3.

nazewnictwo & identyfikowanie gwiazd

daj nam znać, że zdjęcie Crux i wskaźniki z góry tej strony., Poniższe zdjęcie przedstawia ten sam region z zaznaczonymi gwiazdami. Mają również pokazane ich pozorne magnitudo. Crux to konstelacja, jeden z 88 regionów, na które sfera niebieska została podzielona i uzgodniona międzynarodowo przez astronomów. Crux jest najmniejszym z gwiazdozbiorów i jest łatwo rozpoznawalny na południowym niebie. Znane pobliskie Gwiazdy, powszechnie nazywane wskaźnikami, są w rzeczywistości częścią dużego gwiazdozbioru zwanego Centaurem.

teraz możesz zauważyć, że gwiazdy są nazwane za pomocą liter alfabetu greckiego; α, β, γ δ i ε (alfa, beta, gamma, delta, epsilon jest pierwszą piątką), a następnie standardowym trzyliterowym skrótem dla każdej konstelacji (Cru dla Crucis lub Crux i Cen dla Centaurus). Jeśli przyjrzymy się bliżej jasności obserwowanej dla pięciu nazwanych gwiazd w Crux, zauważymy, że najjaśniejsza gwiazda jest oznaczona jako α, Następna β i tak dalej., System ten nazywany jest systemem Bayera, od nazwiska Johanna Bayera, który wprowadził go w 1603 roku. Najjaśniejsza gwiazda w gwiazdozbiorze ma przypisaną literę α, następną β i tak dalej. Wyjątkiem od tej reguły jest &alpha Orionis lub Betelgeuse. W rzeczywistości jest słabsza od β Ori, Rigel o niewielką ilość. Jest to interesujący przypadek historyczny, rozwiązany przez uświadomienie sobie, że Betelgeuse ma lekko przyciemnioną jasność, ponieważ został nazwany w systemie Bayera.,

należy pamiętać o konstelacjach, że gwiazdy w konstelacji zwykle nie są ze sobą fizycznie związane, w przeciwieństwie do gwiazd w gromadach. Fakt, że pojawiają się blisko siebie, jest wyłącznie efektem wyrównania wzdłuż linii wzroku. W rzeczywistości gwiazdy w powyższym regionie są szeroko oddalone od nas, jak pokazano na następnym zdjęciu.

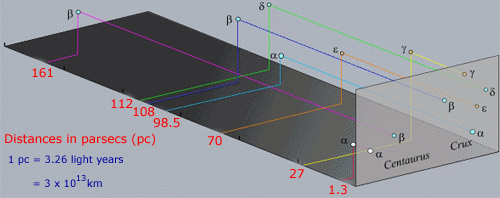
niektóre z jasnych gwiazd, takie jak α Cen, również mają swoją własną nazwę. Syriusz (α Sco) jest jednym z takich przykładów, podczas gdy α Cen jest również nazywany Rigel Kentaurus. Wiele nazw gwiazd pochodzi z języka arabskiego z czasów, gdy zapisy greckie zostały zachowane i opracowane przez astronomów islamskich. Problem z systemem nazewnictwa gwiazd Bayera polega na tym, że w alfabecie greckim są tylko 24 litery, ale jest ich o wiele więcej niż w każdej konstelacji.

większość gwiazd w rzeczywistości nie ma określonej nazwy ani klasyfikacji Bayera., Obecnie astronomowie zestawili ogromne katalogi gwiazd, niektóre z ponad 10 milionami obiektów, więc większość gwiazd ma tylko numer katalogowy. Gwiazdy mogą mieć wiele więcej niż jedną nazwę identyfikacyjną lub numer katalogowy, w zależności od liczby katalogów, w których się znajdują. Gwiazda zmienna δ Cep znana jest również jako HIP 110991, SAO 34508 lub którykolwiek z ponad 30 innych identyfikatorów. Wiele katalogów używa współrzędnych niebieskich, takich jak Rektascensja i Deklinacja do identyfikacji obiektów. Tak więc δ Cep jest znany jako IRAS 22273+5809, CCDM J22292+5825A i AAVSO 2225 + 57., Niewielkie różnice w RA i dec dla katalogów wynikają z prawidłowego ruchu gwiazd i precesji ramki odniesienia.