Share on
Hypothesis Testing
Hypothesis Testing
het belangrijkste doel van statistieken is het testen van een hypothese. U kunt bijvoorbeeld een experiment uitvoeren en vinden dat een bepaald medicijn effectief is bij de behandeling van hoofdpijn. Maar als je dat experiment niet kunt herhalen, zal niemand je resultaten serieus nemen. Een goed voorbeeld hiervan was de ontdekking van koude fusie, die in de vergetelheid raakte omdat niemand in staat was om de resultaten te dupliceren.,
bekijk de video voor een kort overzicht van het testen van hypothesen, of lees hieronder verder:
accepteer statistieken, marketingcookies om deze video te bekijken.
Inhoud (Klik om naar de sectie te gaan):
- Wat is een hypothese?
- Wat is het testen van hypothesen?
- voorbeelden van hypothesetests (één monster Z-Test).
- hypothese Test op een gemiddelde (TI 83).
- Bayesian Hypothesis Testing.
- meer artikelen voor het testen van hypothesen
zie ook:
- hypothesen in één afbeelding
- kritische waarden
- Wat is de nulhypothese?,
hulp nodig bij een huiswerkprobleem? Bekijk onze bijles pagina!
Wat is een hypothese?
Andreas Cellarius hypothese, die de planetaire bewegingen toont.
een hypothese is een gefundeerde gok over iets in de wereld om je heen. Het moet testbaar zijn, hetzij door experiment of observatie. Bijvoorbeeld:
- een nieuw geneesmiddel waarvan u denkt dat het werkt.
- een manier om je te leren dat het misschien beter is.,
- een mogelijke locatie van nieuwe soorten.
- een eerlijkere manier om gestandaardiseerde tests toe te dienen.
het kan echt alles zijn, zolang je het maar op de proef kunt stellen.
Wat is een hypothese Statement?
Als u een hypothese gaat voorstellen, is het gebruikelijk om een statement te schrijven. Je statement ziet er als volgt uit:
“If I…(doe dit met een onafhankelijke variabele)….dan (dit zal gebeuren met de afhankelijke variabele).”
bijvoorbeeld:
- Als I (verlaag de hoeveelheid water die aan kruiden wordt gegeven) dan (de kruiden zullen in grootte toenemen).,
- Als I (patiënten counseling geven naast medicatie) dan (hun totale depressieschaal zal afnemen).
- Als Ik (geef examens op de middag in plaats van 7) dan (student testscores zal verbeteren).
- Als Ik (kijk op deze bepaalde locatie) dan (ik heb meer kans om nieuwe soorten te vinden).
een goede hypothese moet:
- Een “if” En “then” statement bevatten (volgens de Universiteit van Californië).
- omvat zowel de onafhankelijke als de afhankelijke variabelen.
- testbaar zijn door middel van experiment, onderzoek of een andere wetenschappelijk verantwoorde techniek.,
- gebaseerd zijn op informatie uit eerder onderzoek (van u of van iemand anders).
- ontwerpcriteria hebben (voor engineering-of programmeerprojecten).
Wat is het testen van hypothesen?
hypothese testen in statistieken is een manier voor u om de resultaten van een enquête of experiment te testen om te zien of u zinvolle resultaten hebt. Je bent in principe testen of uw resultaten geldig zijn door het uitzoeken van de kans dat uw resultaten zijn gebeurd door toeval., Als uw resultaten toevallig zijn gebeurd, zal het experiment niet herhaalbaar zijn en heeft dus weinig nut.
hypothese testen kan een van de meest verwarrende aspecten zijn voor studenten, vooral omdat voordat je een test kunt uitvoeren, je moet weten wat je nulhypothese is. Vaak, die lastige woord problemen die u worden geconfronteerd met kan moeilijk te ontcijferen., Maar het is makkelijker dan je denkt; alles wat je hoeft te doen is:
- bepaal je nulhypothese,
- geef je nulhypothese aan,
- Kies wat voor soort test je moet uitvoeren,
- steun of weiger de nulhypothese.
Wat is de nulhypothese?
als je de geschiedenis van de wetenschap volgt, is de nulhypothese altijd het geaccepteerde feit. Eenvoudige voorbeelden van nulhypothesen die algemeen als waar worden aanvaard zijn:
- DNA heeft de vorm van een dubbele helix.
- er zijn 8 planeten in het zonnestelsel (exclusief Pluto).,
- het gebruik van Vioxx kan uw risico op hartproblemen verhogen (een geneesmiddel dat nu van de markt is genomen).
hoe geef ik de nulhypothese aan?
u hoeft geen echt experiment of survey uit te voeren in elementaire statistieken (of zelfs een feit als “Pluto is een planeet”te weerleggen!), dus je krijgt woord problemen van real-life situaties. Je moet uitzoeken wat je hypothese is van het probleem. Dit kan een beetje lastiger zijn dan alleen maar uitzoeken wat het geaccepteerde feit is. Met word problemen, u bent op zoek naar een feit dat is nietig te vinden (i. e., iets wat je kunt afwijzen).
voorbeelden van hypothesen # 1: Basisvoorbeeld
een onderzoeker denkt dat als kniechirurgiepatiënten twee keer per week naar fysiotherapie gaan (in plaats van drie keer), hun herstelperiode langer zal zijn. De gemiddelde hersteltijd voor kniechirurgiepatiënten is 8,2 weken.
de hypothese in deze vraag is dat de onderzoeker gelooft dat de gemiddelde hersteltijd meer dan 8,2 weken is. Het kan in wiskundige termen geschreven worden als:
H1: μ > 8.,2
vervolgens moet u de nulhypothese vermelden (zie: hoe de nulhypothese aangeven). Dat gebeurt er als de onderzoeker het mis heeft. In het bovenstaande voorbeeld, als de onderzoeker verkeerd is dan is de hersteltijd minder dan of gelijk aan 8,2 weken. In de wiskunde is dat:
H0 μ ≤ 8,2
toen we de nulhypothese
tien jaar geleden afwees, geloofden we dat er 9 planeten in het zonnestelsel waren. Pluto werd gedegradeerd als een planeet in 2006. De nulhypothese van “Pluto is een planeet “werd vervangen door” Pluto is geen planeet.,”Natuurlijk, het afwijzen van de nulhypothese is niet altijd zo eenvoudig—het moeilijke deel is meestal uitzoeken wat uw nulhypothese is in de eerste plaats.
voorbeelden van hypothesen (één monster Z-Test)
De één monster z-test wordt niet vaak gebruikt (omdat we zelden de werkelijke standaardafwijking van de populatie kennen). Het is echter een goed idee om te begrijpen hoe het werkt, omdat het een van de eenvoudigste tests is die je kunt uitvoeren bij het testen van hypothesen., In de Engelse les moet je de basis (zoals grammatica en spelling) leren voordat je een verhaal kunt schrijven; denk aan één sample z-tests als de basis voor het begrijpen van meer complexe hypothesen testen. Deze pagina bevat twee hypothesen test voorbeelden voor een monster z-tests.
Eén voorbeeld hypothese testen voorbeelden: # 2
accepteer statistieken, marketing cookies om deze video te bekijken.een schoolhoofd van een bepaalde school beweert dat de leerlingen in zijn school boven het gemiddelde intelligentie liggen. Een willekeurige steekproef van dertig studenten IQ scores hebben een gemiddelde score van 112., Is er voldoende bewijs om de bewering van de directeur te ondersteunen? De gemiddelde populatie IQ is 100 met een standaardafwijking van 15.
Stap 1: Geef de nulhypothese op. Het geaccepteerde feit is dat het bevolkingsgemiddelde 100 is, dus: H0: μ = 100.
Stap 2: Geef de alternatieve hypothese. De bewering is dat de studenten bovengemiddelde IQ-scores hebben, dus:
H1: μ> 100.
het feit dat we op zoek zijn naar scores “groter dan” een bepaald punt betekent dat dit een eenzijdige test is.
Stap 3: Teken een afbeelding om u te helpen het probleem te visualiseren.,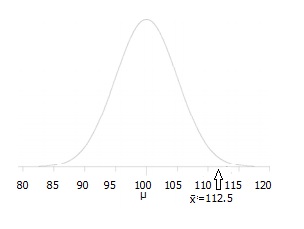
Stap 4: Geef het alfaniveau aan. Als je geen alfaniveau hebt, gebruik dan 5% (0.05).
Stap 5: Zoek het gebied van het afwijzingsgebied (opgegeven door uw alfaniveau hierboven) uit de Z-tabel. Een gebied van .05 is gelijk aan een Z-score van 1,645.
Stap 6: Zoek de teststatistiek met behulp van deze formule: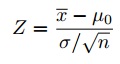 
voor deze reeks gegevens: z= (112.5 – 100) / (15/√30) = 4.56.
Stap 6: als Stap 6 groter is dan Stap 5, wijs de nulhypothese af., Als het minder is dan Stap 5, kun je de nulhypothese niet afwijzen. In dit geval is het groter (4.56 > 1.645), zodat u de null kunt weigeren.
Eén voorbeeld hypothese testen voorbeelden: # 3
accepteer statistieken, marketing cookies om deze video te bekijken.
bloedglucosespiegels voor patiënten met obesitas hebben een gemiddelde van 100 met een standaardafwijking van 15. Een onderzoeker denkt dat een dieet hoog in rauwe maïzena een positief of negatief effect op de bloedsuikerspiegel zal hebben., Een steekproef van 30 patiënten die het rauwe maïzena-dieet hebben geprobeerd, heeft een gemiddeld glucosegehalte van 140. Test de hypothese dat de rauwe maïzena een effect had.
*dit proces wordt veel gemakkelijker gemaakt als u een TI-83 of Excel gebruikt om de Z-score (de “kritische waarde”) te berekenen.,
zie:
- kritische Z-waarde TI 83
- Z-Score in Excel
hypothese testen voorbeelden: Gemiddelde (met TI 83)
U kunt de TI 83 calculator gebruiken voor het testen van hypothesen, maar de calculator zal de nul-en alternatieve hypothesen niet berekenen; dat is aan u om de vraag te lezen en in de calculator in te voeren.
voorbeeldprobleem: een steekproef van 200 personen heeft een gemiddelde leeftijd van 21 jaar met een populatie standaardafwijking (σ) van 5. Test de hypothese dat het populatiegemiddelde 18,9 is bij α = 0,05.
Stap 1: Geef de nulhypothese op., In dit geval is de nulhypothese dat het gemiddelde van de populatie 18,9 is, dus schrijven we:
H0: μ = 18,9
Stap 2: Geef de alternatieve hypothese op. We willen weten of onze steekproef, die een gemiddelde heeft van 21 in plaats van 18,9, echt verschilt van de populatie, daarom is onze alternatieve hypothese:
H1: μ ≠ 18,9
Stap 3: Druk op Stat en druk tweemaal op de rechterpijl om TESTS te selecteren.
Stap 4: Druk op 1 om 1:Z-Test te selecteren…. Druk op ENTER.
Stap 5: Gebruik de pijl naar rechts om statistieken te selecteren.
Stap 6: Voer de gegevens van het probleem in:
μ0: 18.,9
σ: 5
x: 21
n: 200
μ: ≠μ0
Stap 7: pijl naar beneden om te berekenen en druk op ENTER. De calculator toont de p-waarde:
p = 2.87 × 10-9
Dit is kleiner dan onze alfa waarde van .05. Dat betekent dat we de nulhypothese moeten verwerpen.
Bayesiaanse hypothese testen: Wat is het?
afbeelding: Los Alamos National Lab.
Het testen van Bayesiaanse hypothesen helpt om de vraag te beantwoorden: kunnen de resultaten van een test of enquête worden herhaald? waarom kan het ons schelen als een test herhaald kan worden?, Stel dat twintig mensen in hetzelfde dorp leukemie kregen. Een groep onderzoekers vinden dat mobiele telefoontorens zijn de schuld. Uit een tweede onderzoek bleek echter dat de zendmasten niets te maken hadden met de kankercluster in het dorp. In feite ontdekten ze dat de kankers volledig willekeurig waren. Als dat onmogelijk klinkt, kan het echt gebeuren! Clusters van kanker kunnen gewoon bij toeval gebeuren. Er kunnen vele redenen zijn waarom de eerste studie gebrekkig was., Een van de belangrijkste redenen zou kunnen zijn dat ze gewoon geen rekening houden met dat soms dingen willekeurig gebeuren en we gewoon niet weten waarom.
p-waarden.
Het is goed om mensen te laten weten of je studieresultaten solide zijn, of dat ze toevallig hadden kunnen gebeuren. De gebruikelijke manier om dit te doen is om uw resultaten te testen met een p-waarde. Een p waarde is een getal dat je krijgt door het uitvoeren van een hypothese test op uw gegevens. Een P-waarde van 0,05 (5%) of minder is meestal voldoende om te beweren dat uw resultaten herhaalbaar zijn., Er is echter een andere manier om de geldigheid van je resultaten te testen: Bayesiaanse hypothese testen. Dit type testen geeft u een andere manier om de sterkte van uw resultaten te testen.
Bayesian Hypothesis Testing.
traditioneel testen (het type dat u waarschijnlijk tegenkwam in elementaire stats of AP stats) wordt Non-Bayesian genoemd. Het is hoe vaak een uitkomst gebeurt over herhaalde runs van het experiment. Het is een objectief beeld of een experiment herhaalbaar is.het testen van de Bayesiaanse hypothese is een subjectieve kijk op hetzelfde ding., Het houdt rekening met hoeveel vertrouwen je hebt in je resultaten. Met andere woorden, zou je geld inzetten op de uitkomst van je experiment?
verschillen tussen traditionele en Bayesiaanse hypothese testen.
traditioneel testen (niet Bayesiaans) vereist dat u de bemonstering steeds opnieuw herhaalt, terwijl Bayesiaans testen dat niet doet. Het belangrijkste verschil tussen de twee is in de eerste stap van het testen: het stellen van een kans model. In Bayesiaanse testen voeg je voorkennis toe aan deze stap., Het vereist ook gebruik van een posterieure waarschijnlijkheid, dat is de voorwaardelijke waarschijnlijkheid gegeven aan een willekeurige gebeurtenis nadat al het bewijs wordt beschouwd.
argumenten voor Bayesiaanse testen.
veel onderzoekers denken dat het een beter alternatief is voor traditionele tests, omdat het:
- omvat voorkennis over de gegevens.
- houdt rekening met persoonlijke overtuigingen over de resultaten.
argumenten tegen.
- Met inbegrip van eerdere gegevens of kennis is niet gerechtvaardigd.
- het is moeilijk te berekenen in vergelijking met niet-Bayesiaanse testen.,
Back to top
Hypothesis Testing Articles
Basics:
- Wat is Ad Hoc testen?
- Composiethypothese Test
- Wat is een Afstotingsgebied?
- Wat is een Tweestaarttest?
- Hoe moet worden bepaald of een hypothesetest een één-of Tweestaarttest is.
- Hoe te bepalen of een hypothese een Linksstaarttest of een Rechtsstaarttest is.
- Hoe de nulhypothese in statistieken te vermelden.
- Hoe een kritische waarde te vinden.
- Hoe een nulhypothese te ondersteunen of af te wijzen.,
specifieke Tests:
- ANOVA.
- Brunner Munzel Test (Generalized Wilcoxon Test)
- Chi Square Test for Normality
- Cochran-Mantel-Haenszel Test
- F Test
- Granger Causality Test.
- De T-kwadraat
- KPSS-Test van Hotelling.
- Wat is een Waarschijnlijkheidsratio-Test?
- Log rank test.
- MANCOVA
- sequentiële Waarschijnlijkheidsratio Test
- Hoe moet een Tekentest worden uitgevoerd.
- t Test: één monster.
- T-Test: twee monsters.
- Welch ‘ s ANOVA.
- Welch ‘ s Test voor ongelijke varianties.,
- Z-Test: één monster.
- Z-Test: twee proportionele
- Wald-Test.
- Wat is een Acceptatiegebied?
- Hoe de Stelling van Chebyshev te berekenen.
- Beslissingsregel.
- vrijheidsgraden.
- directionele Test
- False Discovery Rate
- Hoe wordt het minst significante verschil berekend.
- niveaus in statistieken.
- Hoe de foutmarge te berekenen.
- gemiddeld verschil (Verschil in gemiddelden)
- het meervoudige Testprobleem.
- Wat is het Neyman-Pearson Lemma?
- één monster mediane Test.,
- REGWF
- Hoe een steekproefgrootte te vinden (algemene instructies).
- Sig 2 (Tailed) betekenis In resultaten
- Wat is een gestandaardiseerde teststatistiek?
- standaardfout
- gestandaardiseerde waarden: voorbeeld.
- Hoe bereken je een T-Score?
- T-Score Vs. A Z. Score.
- testen van één enkel gemiddelde.
- ongelijke steekproefgrootte.
- Uniform meest krachtige Tests.
- Hoe bereken je een Z-Score?
——————————————————————————eeft u hulp nodig met een huiswerk-of testvraag?, Met Chegg Study krijgt u stap-voor-stap oplossingen voor uw vragen van een expert in het veld. Je eerste 30 minuten met een Chegg tutor is gratis!