cumulatieve frequentie
gearchiveerde inhoud
als gearchiveerd geïdentificeerde informatie wordt verstrekt voor referentie -, onderzoeks-of archiefdoeleinden. Het is niet onderworpen aan de webstandaarden van de regering van Canada en is niet gewijzigd of bijgewerkt sinds het werd gearchiveerd. Neem contact met ons op om een ander formaat aan te vragen dan beschikbaar is.,
- Voorbeeld 1-Discrete variabelen
- Voorbeeld 2-continue variabelen
- andere cumulatieve frequentieberekeningen
cumulatieve frequentie wordt gebruikt om het aantal waarnemingen te bepalen dat boven (of onder) een bepaalde waarde in een gegevensverzameling ligt. De cumulatieve frequentie wordt berekend aan de hand van een frequentieverdelingstabel, die kan worden opgebouwd uit stengel-en bladpercelen of rechtstreeks uit de gegevens.
de cumulatieve frequentie wordt berekend door elke frequentie uit een frequentieverdelingstabel op te tellen bij de som van zijn voorgangers., De laatste waarde zal altijd gelijk zijn aan het totaal voor alle waarnemingen, aangezien alle frequenties al bij het vorige totaal zijn opgeteld.
Discrete of continue variabelen
variabelen in elke berekening kunnen worden gekarakteriseerd door de waarde die eraan wordt toegekend. Een discrete variabele bestaat uit afzonderlijke, ondeelbare categorieën. Er kunnen geen waarden bestaan tussen een variabele en zijn buurman. Bijvoorbeeld, als je een klas aanwezigheid geregistreerd van dag tot dag te observeren, kunt u ontdekken dat de klas 29 studenten op een dag en 30 studenten op een andere., Het is echter onmogelijk dat studenten tussen de 29 en 30 jaar aanwezig zijn. (Er is gewoon geen ruimte om waarden tussen deze twee waarden waar te nemen, omdat er geen manier is om 29 en een half studenten te hebben.)
niet alle variabelen worden als discreet gekarakteriseerd. Sommige variabelen (zoals tijd, lengte en gewicht) zijn niet beperkt tot een vaste set van ondeelbare categorieën. Deze variabelen worden continue variabelen genoemd en zijn deelbaar in een oneindig aantal mogelijke waarden. De tijd kan bijvoorbeeld worden gemeten in fractionele delen van uren, minuten, seconden en milliseconden., Dus, in plaats van een race in 11 of 12 minuten te eindigen, kunnen een jockey en zijn paard de finish passeren op 11 minuten en 43 seconden.
het is essentieel om het verschil tussen de twee typen variabelen te kennen om hun cumulatieve frequentie goed te kunnen berekenen.
Voorbeeld 1-Discrete variabelen
de totale rotsklimbertelling van Lake Louise, Alberta werd geregistreerd over een periode van 30 dagen. De resultaten zijn als volgt:
31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56, 4, 54, 39, 52, 35, 51, 63, 42.,e discrete variabelen om:
- Stel een stam-en bladdiagram op (zie het gedeelte over stengel-en bladdiagrammen) met extra kolommen met label frequentie, bovenste waarde en cumulatieve frequentie
- bereken de frequentie van waarnemingen voor elke stam
- zoek de bovenste waarde voor elke stam
- bereken de cumulatieve frequentie door de getallen in de Frequentiekolom op te tellen
- registreer alle resultaten in de grafiek
antwoorden:
- het aantal rotsklimmers varieert van 4 tot 65. Om een stengel en bladplot te produceren, worden de gegevens het best gegroepeerd in klassenintervallen van 10.
elk interval kan zich in de Stamkolom bevinden. De getallen binnen deze kolom vertegenwoordigen het eerste getal binnen het klasse-interval. (Bijvoorbeeld, stam 0 vertegenwoordigt het interval 0-9, stam 1 vertegenwoordigt het interval van 10-19, enzovoort.)
De kolom blad geeft een overzicht van het aantal waarnemingen binnen elk klasse-interval., Bijvoorbeeld, in stam 2 (interval 20-29), worden de drie waarnemingen, 23, 24 en 26, weergegeven als 3, 4 en 6.
De Frequentiekolom geeft het aantal waarnemingen binnen een klasse-interval weer. Bijvoorbeeld, in stam 5 werden negen bladeren (of waarnemingen) gevonden; in stam 1 zijn er slechts twee.
gebruik de Frequentiekolom om de cumulatieve frequentie te berekenen.
- voeg eerst het nummer uit de Frequentiekolom toe aan zijn voorganger. In stam 0 hebben we bijvoorbeeld slechts één waarneming en geen voorgangers. De cumulatieve frequentie is één.,
1 + 0 = 1 - In stam 1 zijn echter twee waarnemingen. Voeg deze twee toe aan de vorige cumulatieve frequentie (één), en het resultaat is drie.
1 + 2 = 3 - in stam 2 zijn er drie waarnemingen. Tel deze drie bij de vorige cumulatieve frequentie (drie) en het totaal (zes) is de cumulatieve frequentie voor Stem 2.
3 + 3 = 6 - ga door met deze berekeningen totdat u alle getallen in de Frequentiekolom hebt opgeteld.
- Registreer de resultaten in de kolom cumulatieve frequentie.,
de kolom met de bovenste waarde toont de waarneming (variabele) met de hoogste waarde in elk van de klassenintervallen. Bijvoorbeeld, in stam 1 vertegenwoordigen de twee waarnemingen 8 en 9 de variabelen 18 en 19. De bovenste waarde van deze twee variabelen is 19.
Tabel 1.,>8 9 2 19 1 + 2 = 3 2 3 4 6 3 26 3 + 3 = 6 3 1 5 5 7 9 5 39 6 + 5 = 11 4 0 1 2 3 5 9 6 49 11 + 6 = 17 5 0 1 1 2 4 4 5 6 7 9 57 17 + 9 = 26 6 0 2 3 5 4 65 26 + 4 = 30
- voeg eerst het nummer uit de Frequentiekolom toe aan zijn voorganger. In stam 0 hebben we bijvoorbeeld slechts één waarneming en geen voorgangers. De cumulatieve frequentie is één.,
- Since these variables are discrete, use the upper values in plotting the graph., Plot de punten om een continue curve genaamd een ogive te vormen.
label de grafiek altijd met de cumulatieve frequentie-overeenkomend met het aantal waarnemingen—op de verticale as.,bel de horizontale as met de andere variabele (in dit geval de totale bergbeklimmer telt) zoals hieronder wordt getoond:
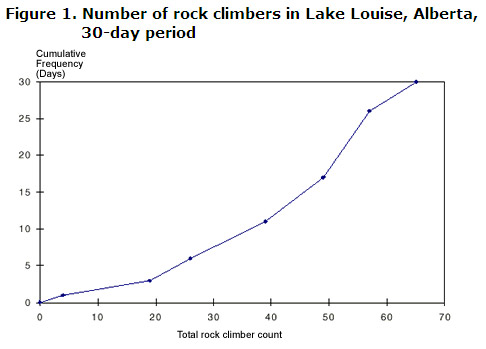
De volgende informatie kan worden verkregen van zowel grafiek of tabel:
- op 11 van de 30 dagen, 39 mensen of minder beklommen de rotsen rond Lake Louise
- op 13 van de 30 dagen, 50 of meer mensen beklommen de rotsen rond Lake Louise
Als een continue variabele wordt gebruikt, kunnen zowel de berekening van de cumulatieve frequentie en het plotten van de grafiek vereisen een iets andere benadering die wordt gebruikt voor een discrete variabele.,
Voorbeeld 2-continue variabelen
gedurende 25 dagen werd de sneeuwhoogte op Whistler Mountain B. C. gemeten (tot op de dichtstbijzijnde centimeter) en als volgt geregistreerd:
242, 228, 217, 209, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257.,
- gebruik bovenstaande continue variabelen om:
- een frequentieverdelingstabel instellen
- zoek de frequentie voor elk klasse-interval
- zoek het eindpunt voor elk klasse-interval
- bereken de cumulatieve frequentie door de getallen in de Frequentiekolom op te tellen
- registreer alle resultaten in de tabel
- gebruik de informatie uit de frequentieverdelingstabel om een cumulatieve frequentiegrafiek uit te tekenen.
antwoorden:
- de metingen van de sneeuwdiepte variëren van 209 cm tot 266 cm., Om de frequentieverdelingstabel te produceren, worden de gegevens het best gegroepeerd in klassenintervallen van elk 10 cm.
in de kolom sneeuwdiepte wordt elk 10 cm-interval van 200 cm tot 270 cm vermeld.
De Frequentiekolom registreert het aantal waarnemingen dat binnen een bepaald interval valt. Deze kolom geeft de waarnemingen in de Tally kolom weer, alleen in numerieke vorm.,
de kolom eindpunt functioneert zoals de kolom met de bovenste waarde van Oefening 1, met de uitzondering dat het eindpunt het hoogste getal in het interval is, ongeacht de werkelijke waarde van elke waarneming. Bijvoorbeeld, in de klasse interval van 210-220, de werkelijke waarde van de twee waarnemingen is 217 en 219. Maar in plaats van 219 wordt het eindpunt 220 gebruikt.
De kolom cumulatieve frequentie geeft het totaal weer van elke frequentie die aan zijn voorganger is toegevoegd.
Tabel 2. Sneeuwhoogte gemeten bij Whistler Mountain, B. C.,e2cd5a9″> 5 240 11 240 to < 250 
7 250 18 250 to < 260 
5 260 23 260 to < 270 
2 270 25
- Because the variable is continuous, the endpoints of each class interval are used in plotting the graph., De geplot punten worden samengevoegd om een ogive te vormen.
onthoud dat de cumulatieve frequentie (aantal waarnemingen) op de verticale y-as wordt vermeld en elke andere variabele (sneeuwdiepte) op de horizontale x-as, zoals weergegeven in Figuur 2.,

de volgende informatie kan worden verkregen uit een grafiek of tabel:
- geen van de 25 dagen sneeuwdiepte minder dan 200 cm
- een van de 25 dagen sneeuwdiepte minder dan 210 cm
- twee van de 25 dagen sneeuwdiepte 260 cm of meer
andere cumulatieve frequentieberekeningen
een andere berekening die kan worden verkregen met behulp van een frequentieverdelingstabel is de relatieve frequentieverdeling. Deze methode wordt gedefinieerd als het percentage waarnemingen dat in elk klasse-interval valt., De relatieve cumulatieve frequentie kan worden gevonden door de frequentie van elk interval te delen door het totale aantal waarnemingen. (Voor meer informatie, zie frequentieverdeling in het hoofdstuk met als titel Het organiseren van gegevens.)
een frequentieverdelingstabel kan ook worden gebruikt om het cumulatieve percentage te berekenen. Deze methode van frequentieverdeling geeft ons het percentage van de cumulatieve frequentie, in tegenstelling tot het percentage van alleen de frequentie.