• historische achtergrond
• schijnbare Magnitude, m
• Absolute Magnitude, m
• het vinden van de afstand tot Sterren – Distance Modulus
• Magnitude/Afstandberekeningen
• naamgeving & het identificeren van sterren

onderzoek de onderstaande foto van het sterveld. Het toont een gebied van de hemel rond het sterrenbeeld Crux, gewoonlijk het Zuiderkruis genoemd. Beweeg uw cursor over de foto om een aantal sterren te identificeren.

welke ster is het helderst?,

als je antwoord hebt gegeven op Alfa (α) Centauri, dan heb je rechts de ster linksonder op de foto. Zoals je kunt zien, toont een fotografisch beeld zoals dit veel meer sterren dan je kunt zien met je blote oog. Toch zijn sommige sterren prominenter dan andere. Bij het kiezen van α Centauri heb je een aantal veronderstellingen gemaakt. Wat waren het?

een foto zoals deze toont heldere sterren als grotere schijven dan zwakkere sterren., Betekent dit dat deze sterren fysiek groter zijn dan de zwakkere sterren op de foto? Onthoud, in het gedeelte over astrometrie hebben we geleerd dat alle sterren behalve onze zon zo ver weg zijn dat ze effectief puntbronnen zijn. Waarom lijken sommigen dan helderder (voor onze ogen) of groter (op foto ‘ s) dan anderen? Wat is helderheid en hoe kunnen we die meten? De antwoorden op deze vragen vormen de focus van deze sectie.,

historische achtergrond

het concept van het meten en vergelijken van de helderheid van sterren kan worden teruggevoerd op de Griekse astronoom en wiskundige Hipparchus (190 – 120 v.Chr.). Hij is een van de grootste astronomen van de oudheid en heeft een catalogus gemaakt van 850 sterren met posities en vergelijkende helderheid., In zijn systeem kregen de helderste sterren een magnitude van 1, de op één na helderste magnitude van 2 en zo verder toegewezen aan de zwakste sterren, net zichtbaar voor het blote oog die magnitude 6 waren. Deze zespuntenschaal kan worden gezien als een rangschikking, eersteklas sterren, de helderste, waren eerste magnitude en dim lage-rate sterren waren zesde magnitude.

De ontdekking van zwakkere sterren met telescopen in de vroege jaren 1600 vereiste dat de schaal werd uitgebreid tot voorbij magnitude 6., De ontwikkeling van visuele fotometers, instrumenten om sterintensiteiten te meten, in de negentiende eeuw door John Herschel en anderen leidde tot de noodzaak voor astronomen om een internationale standaard aan te nemen. Het feit dat ogen verschillen in intensiteit logaritmisch detecteren in plaats van lineair werd ontdekt in de jaren 1830. in 1856 stelde Norman Pogson voor dat een ster van magnitude 1 100 × helderder was dan een ster van magnitude 6. Een verschil van één magnitude was daarom gelijk aan 5√100 = 2,512 keer in helderheid.,

schijnbare Magnitude, m

de schijnbare magnitude, m, van een ster is de magnitude die hij heeft gezien door een waarnemer op aarde.

een zeer helder object, zoals de zon of de maan, kan een negatieve schijnbare magnitude hebben. Hoewel Hipparchus oorspronkelijk de helderste sterren een magnitude van 1 gaf, blijkt dat de helderste ster aan de nachtelijke hemel, Sirius Of α Canis Majoris (CMa), eigenlijk een schijnbare magnitude heeft van m = -1,44. Met de herkalibratie van Hipparchus’ oorspronkelijke waarden is de heldere ster Vega nu gedefinieerd om een schijnbare magnitude van 0,0 te hebben.,

na de telescopische ontdekking van zwakke sterren in de vroege jaren 1600 moest de magnitudeschaal ook worden uitgebreid tot objecten die zwakker zijn dan magnitude 6. De tabel hieronder toont het bereik van schijnbare magnitudes voor hemellichamen.

Object	Schijnbare Omvang
Zon	-26.5
Volle Maan	-12.5
Venus	-4.,3
Mars or Jupiter	-2
Sirius (α CMa)	-1.44
Vega (α Lyr)	0.0
Alnair (α Gru)	1.73
Naked-eye limit	6.5
Binocular limit	10
Proxima Cen	11.,09
Visual limit through 20 cm telescope	14
QSO at redshift z = 2	≈ 20
Cepheid in galaxy M100 observed with HST	26
Galaxy at z = 6 observed with Gemini 8.1 m telescope	28
Limit for James Webb Space Telescope	≥ 30

If a star of magnitude 1 is 2.,512 × helderder dan een ster met magnitude 2 en 100 &keer helderder dan een zesde magnitude ster hoeveel helderder is het dan een ster met magnitude 3? Je moet voorzichtig zijn. Het is niet gewoon 2 × 2.512 verschillend. Je moet onthouden dat een verschil van één magnitude gelijk is aan 5√100 = 2,512. Een verschil van 2 magnitudes dus = 2,5122 = 6,31 × verschil in helderheid.

twee objecten van verschillende magnitudes variëren daarom in helderheid met 2,512 verhoogd tot de kracht van u magnitudeverschil., Als we dit als een vergelijking schrijven, wordt de verhouding van helderheid of intensiteit, IA/IB tussen twee objecten, A en B, met magnitudes mA en mB gegeven door de volgende vergelijking:

laten we een voorbeeld bekijken.

Voorbeeld 1: twee sterren vergelijken.hoeveel helderder is Alnair, schijnbare magnitude van + 1,73 dan Proxima Cen met een magnitude van 11,09?met behulp van vergelijking 4.1 hebben we:

so, vervangend in:

Voorbeeld 2: Hoeveel helderder is de zon dan de volle maan?hiervoor herinneren we uit de tabel hierboven dat de zon een schijnbare magnitude heeft van -26,5 en de volle maan, – 12,5.

met behulp van vergelijking 4.1 krijgen we:

substitueren in geeft ons:

Het is belangrijk om te onthouden dat magnitude gewoon een getal is, het heeft geen eenheden. Het symbool voor schijnbare magnitude is een kleine letter m; Je moet dit duidelijk maken in elk probleem.

Absolute Magnitude, M

Wat zegt het feit dat Sirius een schijnbare magnitude van -1,44 heeft en Betelgeuse een schijnbare magnitude van 0,45 over deze twee sterren? Een andere manier om hierover na te denken is om te vragen waarom Sirius de helderste ster aan de nachtelijke hemel is?, Een ster kan om twee belangrijke redenen helder lijken:

1. het kan intrinsiek licht zijn, dat wil zeggen dat het een krachtige emitter van elektromagnetische straling kan zijn, of
2. het kan zeer dicht bij ons zijn, of beide.

de schijnbare magnitude van een ster hangt daarom deels af van zijn Afstand tot ons. In feite Sirius lijkt helderder dan Betelgeuse juist omdat Sirius is zeer dicht bij ons, slechts 2.6 pc weg terwijl Betelgeuse is ongeveer 160 pc afstand., Het besef dat Sterren niet allemaal veel dezelfde helderheid hebben, betekende dat de schijnbare magnitude alleen niet voldoende was om sterren te vergelijken. Een nieuw systeem dat astronomen in staat zou stellen om sterren direct te vergelijken werd ontwikkeld. Dit systeem heet de absolute magnitude, M.

de absolute magnitude, M, van een ster is de magnitude die een ster zou hebben als hij zich op een afstand van 10 parsecs van ons bevond. Een afstand van 10 pc is puur willekeurig maar nu internationaal overeengekomen door astronomen., De schaal voor absolute magnitude is dezelfde als die voor schijnbare magnitude, dat is een verschil van 1 magnitude = 2,512 keer verschil in helderheid. Deze logaritmische schaal is ook open en unitless. Nogmaals, hoe lager of meer negatief de waarde van M, hoe helderder de ster is. Absolute magnitude is een handige manier om de helderheid van een ster uit te drukken. Zodra de absolute magnitude van een ster bekend is, kun je deze ook vergelijken met andere sterren. Betelgeuse, M = -5,6 is intrinsiek helderder dan Sirius met een M = 1,41.

onze Zon heeft een absolute visuele magnitude van 4,8.,

het vinden van de afstand tot Sterren – Distance Modulus

zoals u zich wellicht herinnert uit het gedeelte over astrometrie, zijn de meeste sterren te ver verwijderd om hun parallax direct te laten meten. Maar als je zowel de schijnbare als de absolute magnitudes van een ster kent, kun je de afstand bepalen. Laten we nog eens kijken naar Sirius en Betelgeuse plus een andere ster genaamd GJ 75.

hoe ver weg is GJ 75? Het is een ongewone ster in die zin dat haar schijnbare en absolute magnitudes hetzelfde zijn. Waarom? De reden is dat het eigenlijk 10 parsecs van ons verwijderd is, dus per definitie moeten de twee magnitudes hetzelfde zijn.,

hoe zit het met Sirius? De schijnbare magnitude is lager (dus helderder) dan de absolute magnitude. Dit betekent dat het dichter bij ons is dan 10 parsecs. Betelgeuse ‘ s schijnbare magnitude is hoger (dus dimmer) dan zijn absolute magnitude, dus het zou nog helderder lijken aan de nachtelijke hemel als het slechts 10 parsecs verwijderd was.

astronomen gebruiken het verschil tussen de schijnbare en absolute magnitude, de distance modulus, als een manier om de afstand tot een ster te bepalen.

• Distance Modulus = M-M.
• Distance modulus is negatief voor sterren dichter dan 10 parsecs.,
• Afstandsmodulus is positief voor sterren verder weg dan 10 parsecs.
• de grootte van de distance modulus bepaalt de werkelijke waarde van de afstand, zodat een ster met distance modulus 1.5 dichter is dan één met een distance modulus van 8.7.

Magnitude/Afstandberekeningen

De afstandsmodulus kan worden gebruikt om de afstand tot een ster te bepalen met behulp van de vergelijking:

waarbij d in parsecs staat. Merk op dat als d = 10 pc dan m en M zijn hetzelfde. (Een formele afleiding van deze vergelijking wordt gegeven in de volgende pagina over helderheid)., De NSW HSC Syllabus formule blad geeft de vergelijking als:

maar dit is gewoon een herwerking van vergelijking 4.2. Je moet comfortabel zijn in het oplossen van deze vergelijking gegeven om het even welke twee van de drie variabelen. Laat het ons weten kijk naar hoe u enkele voorbeelden kunt oplossen.

Voorbeeld 3: gegeven m en d heeft need to find M.
β Crucis (of Mimosa) een schijnbare magnitude van 1,25 en is 108 parsecs verwijderd. Wat is de absolute omvang ervan?

met behulp van vergelijking 4.3 hebben we:

dus β Crucis heeft een absolute magnitude van -3.92
merk op dat deze berekening volledig werkt zodat elke stap expliciet is. (Vergeet niet in het oplossen van magnitude vergelijkingen log verwijst naar logaritmen naar BASIS 10 en niet natuurlijke logaritmen of ln.)

Voorbeeld 4: gegeven m en M, find d.Betelgeuse heeft een schijnbare magnitude van 0,45 en een absolute magnitude van -5,14. Hoe ver is het?
dit probleem vereist dat we vergelijking 4.2 herschrijven om ons d als het onbekende te geven., Dit wordt hieronder getoond:

die kan worden geschreven als:

nu vervangen door:

dus Betelgeuse is ongeveer 130 pc verwijderd.

nogmaals, dit voorbeeld toont volledig werken terwijl u in werkelijkheid mogelijk niet elke stap toont., Het is echter belangrijk dat je je werk op dergelijke problemen duidelijk uitzet, zodat je je algebraïsche manipulatie en je substituties kunt controleren. Het werken met logs en indices kan lastig zijn, dus zorg ervoor dat u weet hoe u deze op uw rekenmachine kunt doen.

Voorbeeld 5: gegeven M en d, vind m.
in de praktijk is dit type probleem minder realistisch voor werkelijke objecten omdat we normaal hun schijnbare magnitudes direct kunnen meten, maar het kan zijn dat we willen berekenen welke schijnbare magnitude een klasse of type object de andere parameters kan hebben gegeven. Nogmaals, beginnend met Vergelijking 4.,3 Laten we bepalen hoe helder een superreus zoals Deneb met een absolute magnitude van -8,73 zou verschijnen als hij 230 parsecs verwijderd was.

dus vervangen in:

dus Deneb zou een schijnbare magnitude van -1.89. Dit zou het helderder maken aan onze nachtelijke hemel dan Sirius (m = -1,44)., In werkelijkheid Deneb is ongeveer 990 pc afstand, hoewel deze waarde heeft een grote onzekerheid.

Voorbeeld 6: Wat als d niet wordt gegeven, maar parallax, p wordt gegeven?dit is eigenlijk heel eenvoudig. Bedenk uit de sectie over astrometrie dat er een directe relatie is tussen Afstand en parallax.

dus u hoeft dit alleen maar in vergelijking 4.2 of 4.3 in te voegen.

Naming & Identifying Stars

laat ons weten dat u de foto van Crux en de Pointers bovenaan deze pagina opnieuw bekijkt., De foto hieronder toont hetzelfde gebied met de prominente sterren gelabeld. Ze hebben ook hun schijnbare grootheden getoond. Crux is een sterrenbeeld, een van de 88 gebieden waarin de hemelbol is opgesplitst en internationaal overeengekomen door astronomen. Crux is eigenlijk de kleinste van de sterrenbeelden en is gemakkelijk te herkennen aan de zuidelijke hemel. De prominente nabijgelegen sterren die gewoonlijk de Pointers worden genoemd, maken eigenlijk deel uit van een groot sterrenbeeld dat Centaurus wordt genoemd.

nu kunt u zien dat de sterren zijn benoemd met behulp van letters uit het Griekse alfabet; α, β, γ δ En ε (Alfa, beta, gamma, delta, Epsilon is de eerste vijf) gevolgd door de standaard drie-letter afkorting voor elk sterrenbeeld (Cru voor Crucis of Crux en Cen voor Centaurus). Als je goed kijkt naar de schijnbare magnitudes voor de vijf genoemde sterren in Crux zul je zien dat de helderste ster α is, de volgende β enzovoort., Dit systeem wordt het Bayer-systeem genoemd, naar Johann Bayer die het in 1603 introduceerde. De helderste ster in een sterrenbeeld krijgt de letter α, de volgende β enzovoort toegewezen. Een uitzondering op deze regel is &alpha Orionis of Betelgeuse. Het is in feite een beetje zwakker dan β Ori, Rigel. Dit is een interessant historisch geval opgelost door het besef dat Betelgeuse lichtjes in helderheid is gedimd sinds het onder het Bayer-systeem werd genoemd.,

een punt om te onthouden over sterrenbeelden is dat de sterren binnen een sterrenbeeld meestal niet fysiek met elkaar geassocieerd zijn, in tegenstelling tot sterren in clusters. Het feit dat dicht bij elkaar verschijnen is puur een uitlijning effect langs de tour lijn van het zicht. In feite zijn de sterren in het gebied hierboven ver van ons gescheiden, zoals te zien is in de volgende afbeelding.

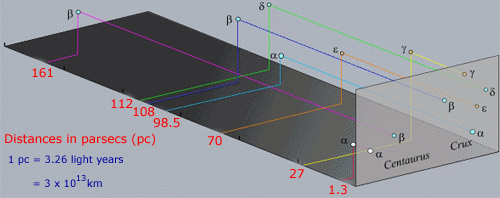
sommige heldere sterren zoals α Cen hebben ook een eigen soortnaam. Sirius (α Sco) is zo ‘ n voorbeeld, terwijl α Cen ook Rigel Kentaurus wordt genoemd. Veel sterrennamen zijn arabisch van oorsprong uit het tijdperk waarin Griekse records werden bewaard en ontwikkeld door Islamitische astronomen. Het probleem met het Bayer-systeem voor het benoemen van sterren is dat er slechts 24 letters in het Griekse alfabet staan, maar dat er veel meer sterren zijn dan in elk sterrenbeeld.

De meeste sterren hebben in feite geen specifieke naam of Bayer-classificatie., Tegenwoordig hebben astronomen enorme catalogi van sterren samengesteld, sommige met meer dan 10 miljoen objecten, dus de meeste sterren hebben alleen een catalogusnummer. Sterren kunnen veel meer dan één identificatienaam of catalogusnummer hebben, afhankelijk van het aantal catalogi waarin ze zich bevinden. De variabele ster, δ Cep bijvoorbeeld is ook bekend als HIP 110991, SAO 34508, of een van meer dan 30 andere identifiers! Veel catalogi maken gebruik van celcoördinaten zoals rechte klimming en declinatie om objecten te identificeren. Dus δ Cep staat bekend als IRAS 22273 + 5809, CCDM J22292+5825A en AAVSO 2225+57., De lichte variaties in RA en dec voor de catalogi ontstaan door de eigenbeweging van de sterren en de precessie van het referentieframe.