Hypotese-Testing
 Det viktigste formålet med statistikken er å teste en hypotese. Du kan For eksempel kjøre et eksperiment og finner ut at et bestemt legemiddel er effektiv ved behandling av hodepine. Men hvis du ikke kan gjenta eksperimentet, ingen vil ta resultatene på alvor. Et godt eksempel på dette var den kalde fusjon discovery, som langsomt dødd i mørket fordi ingen var i stand til å reprodusere resultatene.,
Det viktigste formålet med statistikken er å teste en hypotese. Du kan For eksempel kjøre et eksperiment og finner ut at et bestemt legemiddel er effektiv ved behandling av hodepine. Men hvis du ikke kan gjenta eksperimentet, ingen vil ta resultatene på alvor. Et godt eksempel på dette var den kalde fusjon discovery, som langsomt dødd i mørket fordi ingen var i stand til å reprodusere resultatene.,
Se videoen for en kort oversikt over hypotesetesting, eller les videre nedenfor:
Innhold (Klikk for å hoppe til delen):
- Hva er en Hypotese?
- Hva er Hypotese-Testing?
- hypotesetesting Eksempler (En-Utvalg Z-Test).
- hypotesetest på en Mean (TI-83).
- Bayesiansk hypotesetesting.
- Mer hypotesetesting Artikler
Se også:
- hypotesetestene i Ett Bilde
- Kritiske Verdier
- Hva er nullhypotesen?,
Trenger hjelp med lekser problemet? Sjekk ut vår veiledning side!
Hva er en Hypotese?

Andreas Cellarius hypotese, som viser planetenes bevegelser.
En hypotese er en kvalifisert gjetning om noe i verden rundt deg. Det bør være testbare, enten ved eksperiment eller observasjon. For eksempel:
- En ny medisin som du tror kan fungere.
- En måte å undervise du tror kan være bedre.,
- En mulig plassering av nye arter.
- En mer rettferdig måte å administrere standardiserte tester.
Det kan egentlig være hva som helst så lenge du kan sette den til test.
Hva er en Hypotese Uttalelse?
Hvis du kommer til å foreslå en hypotese, er det vanlig å skrive en uttalelse. Utskriften vil se ut som dette:
«Hvis jeg…(gjør dette til en uavhengig variabel)….deretter (dette vil skje i den avhengige variabelen).»
For eksempel slik:
- Hvis jeg (redusere mengden av vann som er gitt til urter) og deretter (urter vil øke i størrelse).,
- Hvis jeg (gi pasienter rådgivning i tillegg til medisinering) og deretter (deres generelle depresjon skala vil minske).
- Hvis jeg (gi eksamener midt på dagen i stedet for 7), deretter på (student testresultater vil forbedre).
- Hvis jeg (se i denne bestemt plassering), deretter på (jeg er mer sannsynlig å finne nye arter).
En god hypotese uttalelsen skal:
- Ta et «hvis» og «så» resultatregnskap (i henhold til University of California).
- Omfatte både de uavhengige og avhengige variabler.
- Være testbare av eksperimentet, undersøkelse eller annet vitenskapelig lyd teknikk.,
- Være basert på informasjon i tidligere forskning (enten din egen eller noen andres).
- Har design-kriterier (for ingeniør-eller programmering prosjekter).
Hva er Hypotese-Testing?

hypotesetesting i statistikk er en måte for deg å teste den resultatene av en undersøkelse eller et eksperiment for å se om du har meningsfulle resultater. Du er i utgangspunktet å teste om resultatene er gyldige ved å finne ut oddsen for at resultatene har skjedd ved en tilfeldighet., Hvis dine resultater kan ha skjedd ved en tilfeldighet, eksperimentet vil ikke være repeterbare og så har lite bruk.
Hypotese-testing kan være en av de mest forvirrende aspekter for studenter, for det meste fordi før du kan også utføre en test, må du vite hva din nullhypotesen er. Ofte, disse vanskelige ord problemer som du sliter med, kan være vanskelig å tyde., Men det er enklere enn du tror; alt du trenger å gjøre er:
- Figur ut din nullhypotesen,
- oppgi din nullhypotesen,
- Velg hva slags test du trenger for å utføre,
- Enten støtte eller forkaste nullhypotesen.
Hva er nullhypotesen?
Hvis du sporer tilbake historien om vitenskap og forskning, null-hypotesen er alltid akseptert faktum. Enkle eksempler på null-hypoteser som er generelt akseptert som sant er:
- DNA er formet som en dobbel helix.
- Det er 8 planeter i solsystemet (unntatt Pluto).,
- Ta Vioxx kan øke din risiko for hjerte problemer (et stoff som nå er tatt ut av markedet).
Hvordan gjør jeg Staten nullhypotesen?
Du vil ikke være nødvendig å faktisk utføre en ekte eksperiment eller en undersøkelse i elementær statistikk (eller motbevise et faktum som «Pluto er en planet»!), så vil du bli gitt ord problemer fra den virkelige situasjoner i livet. Du trenger å finne ut hva din hypotese er fra problemet. Dette kan være litt mer komplisert enn bare å finne ut hva som er akseptert faktum er. Med word problemer, er du ute etter å finne et faktum som er nullifiable (dvs., noe du kan avvise).
hypotesetesting Eksempler #1: Grunnleggende Eksempel på
En forsker mener at hvis kneet kirurgi pasienter gå til fysioterapi to ganger i uken (i stedet for 3 ganger), deres utvinning perioden vil bli lenger. Gjennomsnittlig utvinning ganger for kneet kirurgi pasienter er 8.2 uker.
hypotesen uttalelse i dette spørsmålet er at forskeren mener gjennomsnittlig utvinning tid er mer enn 8.2 uker. Det kan være skrevet i matematiske termer som:
H1: μ > 8.,2
Neste, vil du trenger å oppgi nullhypotesen (Se: Hvordan staten nullhypotesen). Det er hva som vil skje hvis forskeren er galt. I ovennevnte eksempel, hvis forskeren er feil så er det tid for gjenoppretting er mindre enn eller lik 8.2 uker. I matematikk, som er:
H0 ĩ ≤ 8.2
Avvise nullhypotesen
Ti år siden eller så, vi trodde at det var 9 planeter i solsystemet. Pluto ble degradert som en planet i 2006. Nullhypotesen om «Pluto er en planet» ble erstattet av «Pluto er ikke en planet.,»Selvfølgelig, å avvise nullhypotesen er ikke alltid så lett—den harde delen er vanligvis å finne ut hva dine nullhypotesen er på første plass.
hypotesetesting Eksempler (En-Utvalg Z-Test)
Den ene utvalg z test brukes ikke veldig ofte, fordi vi sjelden vite den faktiske standardavviket). Det er imidlertid en god idé å forstå hvordan det virker som det er en av de enkleste tester du kan utføre i hypotesetesting., I engelsk klassen du fikk lære det grunnleggende (som grammatikk og stavemåte) før du kan skrive en historie; tenke på et utvalg z-tester som grunnlag for å forstå mer komplekse hypotesetesting. Denne siden inneholder to hypotesetesting eksempler for ett utvalg z-tester.
En Prøve hypotesetesting Eksempler: #2
En rektor ved en bestemt skole hevder at elevene i skolen er over gjennomsnittlig intelligens. Et tilfeldig utvalg av tretti studenter IQ-score har en gjennomsnittlig score på 112., Er det tilstrekkelig bevis for å støtte den viktigste krav? Det betyr befolkningen IQ er 100 med et standardavvik på 15.
Trinn 1: Stat nullhypotesen. Den aksepterte faktum er at befolkningen mener er 100, så: H0: μ=100.
Trinn 2: Stat den Alternative Hypotesen. Kravet er at studentene har over gjennomsnittlig IQ score, slik:
H1: μ > 100.
Det faktum at vi er ute for score «større enn» et visst punkt betyr at dette er en one-tailed test.
Trinn 3: Tegn et bilde for å hjelpe deg med å visualisere problemet.,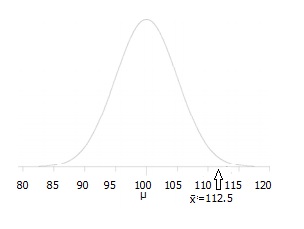
Trinn 4: Staten alfa-nivå. Hvis du ikke er gitt en alpha-nivå, bruk 5% (0.05).
Trinn 5: Finn avvisning region-området (gitt av din alpha-nivå over) fra z-tabellen. Et område av .05 er lik en z-score på 1.645.
Trinn 6: Finn teststatistikk ved hjelp av denne formelen: 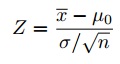
For dette settet av data: z= (112.5 – 100) / (15/√30) = 4.56.
Trinn 6: Hvis Trinn 6 er større enn Trinn 5, forkaster nullhypotesen., Hvis det er mindre enn Trinn 5, kan du ikke avvise nullhypotesen. I dette tilfellet er det større (4.56 > 1.645), så du kan avvise null.
En Prøve hypotesetesting Eksempler: #3
blodsukker nivåer for overvektige pasienter har et gjennomsnitt på 100 med et standardavvik på 15. En forsker mener at en diett høy i raw cornstarch vil ha en positiv eller negativ effekt på blodsukkernivået., Et utvalg av 30 pasienter som har prøvd den rå cornstarch kosthold har en gjennomsnittlig glukose nivå på 140. Teste hypotesen om at raw cornstarch hadde en effekt.
*Denne prosessen er gjort mye enklere hvis du bruker en TI-83-eller Excel for å beregne z-score («kritisk verdi»).,
Se:
- Kritisk z-verdi TI 83
- Z-Score i Excel
hypotesetesting Eksempler: Mean (ved Hjelp av TI-83)
Du kan bruke TI-83 kalkulator for hypotesetesting, men kalkulatoren vil ikke finne ut null og alternative hypoteser; det er opp til deg å lese spørsmålet og taste det inn i kalkulatoren.
Eksempel problem: Et eksempel på 200 personer har en gjennomsnittlig alder av 21 år med en befolkning standardavvik (σ) av 5. Test av hypotesen at befolkningen mener er 18.9 på α = 0.05.
Trinn 1: Stat nullhypotesen., I dette tilfellet, nullhypotesen er at befolkningen mener er 18.9, så vi skrive:
H0: μ = 18.9
Trinn 2: Stat den alternative hypotesen. Vi ønsker å vite om vårt eksempel, som har et gjennomsnitt på 21 i stedet for 18.9, virkelig er forskjellig fra befolkningen, derfor vårt alternative hypotesen:
H1: μ ≠ 18.9
Trinn 3: Trykk Stat og trykk høyre piltast to ganger for å velge TESTER.
Trinn 4: Trykk 1 for å velge 1:Z-Test…. Trykk på ENTER.
Trinn 5: Bruk høyre pil for å velge Statistikk.
Trinn 6: skriv Inn data fra problemet:
μ0: 18.,9
σ: 5
x: 21
n: 200
μ: ≠μ0
Trinn 7: Pil ned for å Beregne og trykk på ENTER. Kalkulatoren viser p-verdi:
p = 2.87 × 10-9
Dette er mindre enn våre alpha verdi .05. Det betyr at vi bør forkaste nullhypotesen.
Bayesiansk hypotesetesting: Hva er det?
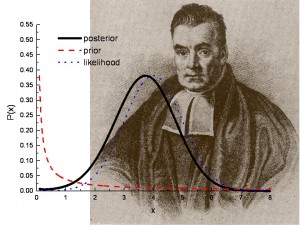
Bilde: Los Alamos National Lab.
Bayesiansk hypotesetesting bidrar til å besvare spørsmålet: Kan resultatene fra en test eller undersøkelse gjentas?
Hvorfor vi bryr oss om en test kan gjentas?, La oss si tjue mennesker i den samme landsbyen kom ned med leukemi. En gruppe forskere finne at celle-telefon tårn er å klandre. Men en annen studie fant at celle-telefon tårn hadde ingenting å gjøre med cancer cluster i landsbyen. Faktisk, de fant at kreft var helt tilfeldig. Hvis det høres umulig, er det faktisk kan skje! Klynger av kreft kan skje bare ved en tilfeldighet. Det kan være mange grunner til at den første studien var feil., En av de viktigste grunnene kan være at de bare ikke ta hensyn til at noen ganger kan ting skje tilfeldig, og vi vet bare ikke hvorfor.
P-Verdier.
Det er god vitenskap å la folk få vite om ditt studium resultater er fast, eller om de kan ha skjedd ved en tilfeldighet. Den vanlige måten å gjøre dette på er å teste resultatene dine med en p-verdi. En p-verdi er et nummer som du får ved å kjøre en hypotesetest på din data. En P-verdi på 0,05 (5%) eller mindre er vanligvis nok til å hevde at resultatene er repeterbare., Men, det er en annen måte å teste gyldigheten av resultatene: Bayesiansk hypotesetesting. Dette er en type test som gir deg en annen måte å teste styrken av resultater.
Bayesiansk hypotesetesting.
Tradisjonell testing (den typen du trolig kom over i elementær statistikk eller AP statistikk) er kalt Ikke-Bayesiansk. Det er hvordan du ofte et resultat som skjer over gjentatte kjøringer av eksperimentet. Det er en objektiv vurdering av om et eksperiment er repeterbare.
Bayesiansk hypotesetesting er en subjektiv oppfatning av det samme., Det tar hensyn til hvor stor tro du har på dine resultater. Med andre ord, ville du satse penger på utfallet av eksperimentet?
Forskjeller Mellom Tradisjonelle og Bayesiansk hypotesetesting.
Tradisjonell testing (Ikke Bayesiansk) krever at du gjenta prøvetaking over og over, mens Bayesiansk testing ikke. Den viktigste forskjellig mellom de to er i første trinn av testing: om en sannsynlighet modell. I Bayesiansk testing du legge til forkunnskaper til dette trinnet., Det krever også bruk av en bakre sannsynlighet, som er betinget sannsynlighet gitt til en tilfeldig hendelse etter at alle bevisene er vurdert.
Argumenter for Bayesiansk Testing.
Mange forskere mener at det er et bedre alternativ til tradisjonell testing, fordi det:
- Har tidligere kunnskap om data.
- Tar hensyn til personlige oppfatninger om resultater.
Argumenter mot.
– >
- Inkludert tidligere data eller kunnskap ikke er forsvarlig.
- Det er vanskelig å beregne i forhold til ikke-Bayesianske testing.,
Tilbake til toppen
hypotesetesting Artikler
Grunnleggende:
- Hva er Ad Hoc Testing?
- Kompositt hypotesetest
- Hva er en Avvisning Regionen?
- Hva er en To-Tailed Test?
- Hvordan å Avgjøre om en hypotesetest er en Tailed-Test eller en To Tailed Test.
- Hvordan å Avgjøre om en Hypotese er en Venstre-Tailed-Test eller en Høyre-Tailed Test.
- Hvordan Staten nullhypotesen i Statistikken.
- Hvordan Finne en Kritisk Verdi.
- Hvordan for å Støtte eller Avvise en Null-Hypotese.,
Spesifikke Tester:
- ANOVA.
- Brunner Munzel Test (Generalisert Wilcoxon Test)
- Chi-Kvadrat-Test for Normalitet
- Cochran-Mantel-Haenszel Test
- F-Test
- Granger kausalitetstest.
- Hotelling T-Squared
- KPSS Test.
- Hva er en Likelihood-Ratio-Test?
- Logg rank test.
- MANCOVA
- Sekvensiell Sannsynlighet Ratio Test
- Hvordan å Kjøre et Tegn Test.
- T-Test: ett eksempel.
- T-Test: To utvalg.
- Welch ‘ s ANOVA.
- Welch ‘ s Test for Ulik Avvik.,
- Z-Test: ett eksempel.
- Z-Test: To Andel
- Wald-Testen.
- Hva er en Aksept Regionen?
- Hvordan å Beregne Chebyshev Teorem.
- Avgjørelse Regelen.
- Grader av Frihet.
- Retningsbestemt Test
- False Discovery Rate
- Hvordan å beregne Minst Betydelig Forskjell.
- Nivåer i Statistikken.
- Hvordan å Beregne feilmarginen.
- Mean Difference (Forskjell i Måte)
- Flere Testing Problem.
- Hva er Neyman-Pearson Lemma?
- Et Eksempel Median Test.,
- REGWF
- Hvordan for å Finne et Eksempel Størrelse (Generelle Instruksjoner).
- Sig 2(Tailed) betyr i resultater
- Hva er en Standardisert Test Statistikk?
- Hvordan for å Finne Standard Feil
- Standardiserte verdier: Eksempel.
- Hvordan å Beregne en T-Score.
- T-Score Vs. en Z-Score.
- Testing av en Enkelt Mener.
- Ulik Eksempel Størrelser.
- Jevnt Kraftigste Tester.
- Hvordan å Beregne en Z-Score.
——————————————————————————
Trenger hjelp med lekser eller test spørsmål?, Med Chegg Studere, kan du få trinn-for-trinn-løsninger til dine spørsmål fra en ekspert på feltet. De første 30 minutter med en Chegg veileder er gratis!