- Historisk Bakgrunn
- store halvakse, m
- Absolutte Magnitude, M
- for å Finne Avstanden til Stjerner – Avstand Modulus
- Omfang/Distanse Beregninger
- Navn & Identifisere Stjerner
Studere stjerners feltet fotografi vises nedenfor. Det viser en region av himmelen rundt den konstellasjonen Crux, ofte kalt «Southern Cross». Flytt markøren over bildet for å identifisere noen stjerner.
Som star er smarteste?,
– >

Hvis du svarte Alfa (α) Centauri, star nederst til venstre på bildet du har rett. Som du kan se, er et fotografisk bilde, som viser mange flere stjerner enn det du kan se med dine uten hjelp øye. Likevel noen stjerner er mer fremtredende enn andre. I å velge alpha Centauri du har gjort noen forutsetninger. Hva ble de?
Et fotografi som viser dette lyse stjerner som større disker enn svakere stjerner., Betyr dette at disse stjernene er fysisk større enn den svakere stjerner i bildet? Husk, i avsnittet om astrometry vi har lært at alle andre stjerner enn vår egen Sol er så langt at de er effektivt punktkilder. Så hvorfor noen ser lysere (til våre øyne) eller større (på bilder) enn andre? Hva som faktisk er lysstyrke og hvordan kan vi måle det? Svarene på disse spørsmålene danner fokus på denne delen.,
Historisk Bakgrunn

konseptet for å måle og sammenligne lysstyrken til stjerner kan spores tilbake til den greske astronomen og matematikeren Hipparchus (190 – 120 F.KR.). En av de største astronomer i antikken, han er kreditert med å produsere en katalog over 850 stjerner med posisjoner og komparativ brightnesses., I sitt system, de klareste stjernene ble tildelt en størrelsesorden på 1, neste smarteste størrelsesorden 2 og så videre til den fjerneste stjerner, bare synlig for egen hjelp øye som var i størrelsesorden 6. Dette seks-punkts skala kan være tenkt som en rangering, første-rate stjerner, og den lyseste, var det første omfang og dim lav pris stjernene var sjette størrelsesorden.
oppdagelsen av svakere stjerner med teleskoper i begynnelsen av 1600-tallet nødvendig skalaen utvides utover magnitude 6., Utvikling av visuell fotometre, instrumenter for å måle stellar intensiteter, i det nittende århundre av John Herschel og andre blir bedt om behovet for astronomer å vedta en internasjonal standard. Det faktum at øynene oppdage forskjeller i intensitet logaritmisk snarere enn lineært ble oppdaget i 1830-årene. I 1856 Norman Pogson foreslått som en stjerne i størrelsesorden 1 var 100 × lysere enn en stjerne i størrelsesorden 6. En forskjell av en størrelsesorden var derfor lik 5√100 = 2.512 ganger i lysstyrke.,
store halvakse, m
De store halvakse, m, av en stjerne er den størrelsesorden at det har så sett av en observatør på Jorden.
En svært lyse objekt, for eksempel Solen eller Månen kan ha en negativ store halvakse. Selv om Hipparchus opprinnelig tildelt de klareste stjernene til å ha en styrke på 1 mer forsiktig sammenligningen viser at den sterkeste stjernen på nattehimmelen, Sirius eller α Canis Majoris (CMa) faktisk har en tilsynelatende omfanget av m = -1.44. Med rekalibrering av Hipparchus’ opprinnelige verdiene den lysende stjerne Vega er nå definert til å ha en tilsynelatende magnitude på 0.0.,
Følgende teleskopiske oppdagelsen av svake stjerner i begynnelsen av 1600-tallet magnitude skalaen har også måtte bli utvidet til objekter svakere enn magnitude 6. Tabellen nedenfor viser omfanget av relativ styrke for himmellegemer.
| Objektet | Tilsynelatende Størrelsesorden |
|---|---|
| Sun |
-26.5
|
| Full Moon |
-12.5
|
| Venus |
-4.,3
|
| Mars or Jupiter |
-2
|
| Sirius (α CMa) |
-1.44
|
| Vega (α Lyr) |
0.0
|
| Alnair (α Gru) |
1.73
|
| Naked-eye limit |
6.5
|
| Binocular limit |
10
|
| Proxima Cen |
11.,09
|
| Visual limit through 20 cm telescope |
14
|
| QSO at redshift z = 2 |
≈ 20
|
| Cepheid in galaxy M100 observed with HST |
26
|
| Galaxy at z = 6 observed with Gemini 8.1 m telescope |
28
|
| Limit for James Webb Space Telescope |
≥ 30
|
If a star of magnitude 1 is 2.,512 × lysere enn en stjerne i størrelsesorden 2 og 100 &ganger sterkere enn en sjette størrelsesorden stjerners hvor mye lysere er det enn en stjerne av størrelsesorden 3? Du må være forsiktig her. Det er ikke bare 2 × 2.512 forskjellige. Du må huske at en forskjell på en størrelsesorden tilsvarer 5√100 = 2.512. En forskjell på 2 storleikar derfor = 2.5122 = 6.31 × forskjellen i lysstyrke.
To objekter av forskjellige størrelsene kan derfor variere noe i lysstyrke ved 2.512 opphøyd i deg størrelsesorden forskjell., Hvis vi skriver dette som en ligning, forholdet mellom lysstyrken eller intensitet, IA/IB mellom to objekter A og B, med størrelsene mA og mB er gitt ved følgende ligning:
La oss se på et eksempel.
Eksempel 1: Sammenligning av to stjerner.
Hvor mye lysere er Alnair, tilsynelatende magnitude på +1.73 enn Proxima Cen med en styrke på 11.09?
ved Hjelp av ligning 4.1 har vi:
så, erstatter i:
Eksempel 2: Hvor mye lysere er Solen enn fullmånen?
For dette vi husker fra tabellen ovenfor at Solen har en tilsynelatende omfanget av -26.5 og fullmåne, – 12.5.
Så ved hjelp av ligning 4.1 får vi:
erstatter i gir oss:
Det er viktig å huske på at omfanget er rett og slett et nummer, det har ikke noen enheter. Symbolet for store halvakse er en bokstav m, må du gjøre dette klart i noe problem.
Absolutte Magnitude, M
Hva betyr det faktum at Sirius har en tilsynelatende omfanget av -1.44 og Betelgeuse en tilsynelatende magnitude på 0,45 fortelle oss om disse to stjerner? En annen måte å tenke på om dette er å spørre hvorfor er Sirius den sterkeste stjernen på nattehimmelen?, En stjerne kan vises lyse for to hovedgrunner:
- Det kan være iboende lysende, er at det kan være en kraftig utslipper av elektromagnetisk stråling, eller
- Det kan være veldig nær oss, eller begge deler.
De store halvakse av en stjerne derfor delvis avhenger dens avstand fra oss. Faktisk Sirius lysere enn Betelgeuse nettopp fordi Sirius er veldig nær oss, bare 2.6 pc unna, mens Betelgeuse er ca 160 pc fjernt., Forståelsen av at stjerner ikke alle har mye den samme glød som betydde at store halvakse alene ikke var tilstrekkelig for å sammenligne stjerner. Et nytt system som gjorde det mulig for astronomer å direkte sammenligne stjerner ble utviklet. Dette systemet kalles den absolutte magnitude, M.
Den absolutte magnitude, M, av en stjerne er den størrelsesorden at stjernen måtte ha om det var i en avstand på 10 parsecs fra oss. En avstand av 10 pc-er rent tilfeldig, men nå internasjonalt avtalte av astronomer., Skalaen for absolutte størrelsen er den samme som for tilsynelatende magnitude, at det er en forskjell på 1 størrelsesorden = 2.512 ganger forskjellen i lysstyrke. Dette logaritmisk skala er også open-ended og unitless. Igjen, lavere eller mer negative verdien til M, den lysere stjerne er. Absolutte magnitude er en praktisk måte å uttrykke den lysstyrken til en stjerne. Når det absolutte omfanget av en stjerne er kjent kan du også sammenligne den med andre stjerner. Betelgeuse, M = -5.6 er egentlig mer skinnende enn Sirius med en M = 1.41.
Vår egen Sol har en absolutt visuelle omfanget av 4.8.,
Finn Avstanden til Stjerner – Avstand Modulus
Som du kanskje husker fra avsnittet om astrometry, de fleste stjernene er for langt til å ha sin parallax målt direkte. Likevel, hvis du vet både relativ og absolutt storleikar for en stjerne du kan bestemme avstand. La oss igjen se på Sirius og Betelgeuse pluss en annen stjerne kalt GJ 75.
Hvor langt unna er GJ 75? Det er en uvanlig stjerne i at dens åpenbare og absolutte størrelsene er de samme. Hvorfor? Årsaken er at det er faktisk 10 parsecs fjernt fra oss, så er de per definisjon sine to størrelsene må være det samme.,
Hva om Sirius? Dens store halvakse er lavere (derfor lysere) enn sin absolutte styrke. Dette betyr at det er nærmere enn 10 parsecs til oss. Betelgeuse er store halvakse er høyere (derfor dimmer) enn sine absolutte magnitude så det ser enda lysere på nattehimmelen hvis det var bare 10 parsecs fjernt.
Astronomer bruker forskjellen mellom relativ og absolutt størrelse, avstand modulus, som en måte av de terming avstanden til en stjerne.
- Avstand Modulus = m – M.
- Avstand modulus er negative for stjerner nærmere enn 10 parsecs.,
- Avstand modulus er positivt for stjerner lenger unna enn 10 parsecs.
- størrelsen på avstand modulus bestemmer den faktiske verdien av avstand, slik at en stjerne av avstand modulus 1.5 er nærmere enn en med en avstand modulus av 8.7.
Omfang/Distanse Beregninger
avstanden modulus kan brukes til å bestemme avstanden til en stjerne ved å bruke ligning:
hvor d er i parsecs. Vær oppmerksom på at hvis d = 10 pc deretter m og M er den samme. (En formell avledning av denne ligningen er gitt på neste side på lysmengde)., NSW HSC Pensum formelark gir ligningen som:
men dette er rett og slett en omarbeiding av ligning 4.2. Du bør være komfortabel med å løse denne ligningen gitt to av de tre variablene. La oss se på hvordan du kan løse noen eksempler.
Eksempel 3: Gitt m og d, trenger å finne M.
β Crucis (eller Mimosa) har en tilsynelatende størrelsesorden 1,25 og er 108 parsecs fjernt. Hva er dens absolutte størrelse?
ved Hjelp av ligning 4.3 har vi:
så β Crucis har en absolutt magnitude på -3.92
Merk denne beregningen har vist full fungerer slik at hvert trinn er eksplisitt. (Husk å løse størrelsesorden ligninger logg refererer til logaritmer til base 10 og ikke naturlige logaritmer eller ln.)
Eksempel 4: Gitt m og M, finner d.
Betelgeuse har en tilsynelatende magnitude på 0,45 og en absolutt magnitude på -5.14. Hvor langt unna er den?
Dette problemet krever oss til å omskrive likning 4.2 å gi oss d som ukjent., Dette er vist nedenfor:
som kan skrives som:
nå erstatte i:
så Betelgeuse er ca 130 pc fjernt.
Igjen, dette eksemplet viser fullføre arbeidet mens det i virkeligheten kan du ikke vise alle trinn., Det er imidlertid også viktig at du setter dine arbeider på slike problemer ut tydelig, slik at du kan sjekke din algebraisk manipulasjon og erstatninger. Arbeider med stokker og indekser kan være vanskelig, så sørg for at du vet hvordan å gjøre disse på kalkulatoren.
Eksempel 5: Gitt M og d, finn m.
I praksis er denne type problem er mindre realistisk for selve objektene som vi normalt kan måle deres tilsynelatende størrelsen direkte imidlertid kan det være at vi ønsker å beregne hvor store halvakse en klasse eller type av objekt kan ha gitt den andre parametre. Igjen, fra og med ligningen 4.,3 la oss finne ut hvor lyst et supergiant som Deneb med en absolutt magnitude på -8.73 ville se ut hvis det var 230 parsecs unna.
så å erstatte i:
så Deneb ville ha en tilsynelatende omfanget av -1.89. Dette ville gjøre det lysere i vår nattehimmelen enn Sirius (m = -1.44)., I virkeligheten Deneb er om 990 pc fjernt selv om denne verdien har en stor usikkerhet.
Eksempel 6: Hva om d er ikke gitt, men parallax, p er gitt?
Dette er faktisk veldig rett frem. Husker fra avsnittet om astrometry at det er en direkte sammenheng mellom avstand og parallax.
så du trenger bare å sette dette inn i ligningen, 4.2 eller 4.3.
Navn & Identifisere Stjerner
La oss se det bildet av Crux og Tips fra toppen av denne siden., Bildet nedenfor viser det samme region med fremtredende stjerner-merket. De har også deres tilsynelatende størrelsen vises. Crux er en konstellasjon, en av 88 regioner som den himmelske sfære har blitt brutt opp i og som er avtalt internasjonalt av astronomer. Crux er faktisk den minste av de konstellasjoner og er lett identifiseres i den sørlige himmel. Den fremtredende nærliggende stjerner ofte kalt Pekere er faktisk en del av en stor konstellasjon kalt Centaurus.
– >

Nå kan du legge merke til at stjernene er navngitt ved hjelp av bokstaver fra det greske alfabetet; α, β, γ δ og ε (alpha, beta, gamma, delta, epsilon å være de første fem) etterfulgt av standard forkortelse på tre bokstaver for hver konstellasjon (Cru for Crucis, eller Crux og Cen for Centaurus). Hvis du ser nøye på den tilsynelatende størrelsene for de fem navngitte stjerner i Kjernen vil du se at den sterkeste stjernen er merket α, neste β og så videre., Dette systemet er kalt Bayer-systemet, etter at Johann Bayer, som introduserte den i 1603. Den sterkeste stjernen i stjernebildet er tilordnet bokstaven α, neste β og så videre. Et unntak fra denne regelen er &alpha Orionis eller Betelgeuse. Det er faktisk svakere enn β Ori, Rigel med en liten mengde. Dette er et interessant historisk saken ble løst ved realisasjon som Betelgeuse har tonet ned litt i lysstyrke siden den ble kalt under Bayer system.,
Ett punkt å huske om konstellasjoner er at stjernene i et stjernebilde er ikke vanligvis er fysisk forbundet med hverandre, i motsetning til stjernene i klynger. Det faktum som vises tett sammen er kun en justering effekt sammen tour linje av syne. Faktisk, stjernene i regionen ovenfor er mye atskilt i avstand fra oss, som vist på neste bilde.
– >
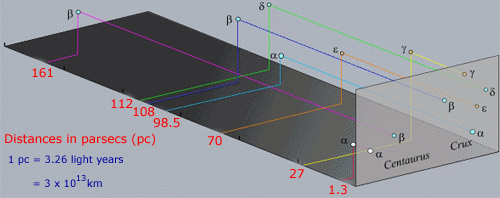
Noen av de lyse stjerner som α Cen også har sine egne spesifikke navn. Sirius (α Sco) er en slike eksempler, mens α Cen er også kalt Rigel Kentaurus. Mange stjerners navn er arabisk opprinnelse fra den tid da gresk poster ble bevart og utviklet av Islamske astronomer. Problemet med Bayer system of naming stjerner er at det er bare 24 bokstaver i det greske alfabetet, men det er mange flere stjerner enn det som er i hver konstellasjon.
de Fleste stjerner faktisk ikke har et bestemt navn eller Bayer klassifisering., I disse dager astronomer har samlet enorme kataloger av stjerner, noen med over 10 millioner objekter, slik at de fleste stjerner har bare et katalognummer. Stjerner kan ha mange flere enn en identifikasjon navn eller katalognummer, avhengig av antall kataloger de er i. Den variable stjernen, δ Cep for eksempel er også kjent som HIP 110991, SAO 34508, eller noen av mer enn 30 andre identifikatorer! Mange kataloger utnytte celestiale koordinatene slik som Høyre Ascension og Misvisning for å identifisere objekter. Dermed δ Cep er kjent som IRAS 22273+5809, CCDM J22292+5825A og AAVSO 2225+57., Utslagene i RA og desember for kataloger oppstår på grunn av den riktige bevegelsene av stjernene og presesjon av referanse ramme.