ACT 수학 연습

에 직면하게 될 6 가지 질문 유형 이러한 질문에 대한 계산기를 사용할 수 있습니다. 선택한 문제에 대해 계산기를 사용할 수도 있지만 문제 중 일부는 계산기를 사용하지 않고도 가장 잘 수행 할 수 있습니다. 나는 이것을 할 수 없다. 무엇을 가장 큰 가치의 x 를 해결하는 방정식 x2-4+3=0

(A)1(B)2(C)3(D)4(E)5
대답을 볼

답변:(G)
경우 하나의 조각에 대한 정보를 원,모든 것을 찾을 수 있습니다 다른 당신은 필요합니다., 원 A 의 면적은 16π 이고 A=π r2 이므로 원 A 의 반지름은 4 여야합니다. 원 B 의 반지름이 원 A 의 절반 인 경우 원 B 의 반지름은 2 여야합니다. 그런 다음 c=2π r=2π r(2)=4π 또는 선택(G)으로 원 B 의 원주를 찾습니다.

대답을 볼

3. 말씀에는 매,얼마나 많은 방법이 가능한자 없는 경우에는 반복하고자 W 가야 하나요?

(A)5(B)15(C)24(D)120(E)650

대답을 참조하십시오

4., 방정식 10x+2x=y+6 으로 표현되는 선의 기울기는 무엇입니까?
(F)10(G)12(H)14(J)15(K)16

답을 참조하십시오

5. 에 삼각형 아래의 탄 표시각 같

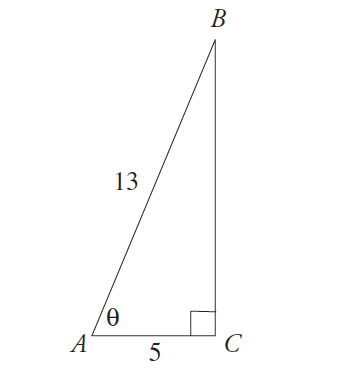
(A)5⁄12(B)12⁄13(C)17⁄12(D)12⁄5(E)3

답변:(D)
를 사용하여 방정식에 접=대/인접해 있습니다. 먼저 될 수 있습니다 여기에 해결하는 알 수없는 쪽지만,가까이 보면 각도 표시입니다., 그것의 인접한면은 5 이며,그 각도의 접선은 5 의 분모를 가져야 함을 의미합니다. (D)만 가지고 있으므로 작동 할 수있는 유일한 대답입니다. 당신이 경우 해결하기 위해 찾을 수면,기억의 피타고라스의 세 배 이 5:12:13 삼각형,그래서 알 수없는 면이어야 합 12.이 문제를 해결하려면 어떻게해야합니까?