仮説検定

統計の主な目的は、仮説をテストすることです。 たとえば、実験を実行し、特定の薬が頭痛の治療に有効であることがわかります。 しかしその実験を繰り返すことができなければ誰もあなたの結果を真剣に取らない。 これの良い例は、誰も結果を複製することができなかったので、あいまいになった常温核融合の発見でした。,

仮説検定の概要については、ビデオを見るか、以下を読んでください：

内容（クリックするとセクションにスキップします）：

1. 仮説とは何ですか？
2. 仮説検定とは何ですか？
3. 仮説検定の例（一つのサンプルZテスト）。
4. 平均に対する仮説検定（TI83）。
5. ベイズ仮説検定。
6. その他の仮説検定の記事

も参照してください：

• 一つの画像での仮説検定
• 臨界値
• 帰無仮説とは何ですか？,

宿題の問題で助けが必要ですか？ 私たちの家庭教師のページをチェック！

仮説とは何ですか？

惑星の動きを示すアンドレアス-セラリウス仮説。

仮説は、あなたの周りの世界の何かについての教育された推測です。 実験または観察のいずれかによってテスト可能であるべきである。 たとえば、

• あなたが働くかもしれないと思う新しい薬。
• あなたが考える教え方が良いかもしれません。,
• 新しい種の可能性のある場所。
• 標準化されたテストを管理するためのより公平な方法。

テストに入れることができる限り、本当に何でもかまいません。

仮説文とは何ですか？

仮説を提案する場合は、声明を書くのが通例です。 あなたのステートメントは次のようになります：
“If I…（これを独立変数に行う）….それから（これは従属変数に起こります）。”
例えば：

• もし私が（ハーブに与えられた水の量を減らす）ならば（ハーブのサイズが大きくなります）。,
• もし私が（投薬に加えて患者にカウンセリングを与える）なら（彼らの全体的なうつ病のスケールは減少する）。
• もし私が（7の代わりに正午に試験をする）なら（学生のテストの得点は改善されます）。
• 私が（この特定の場所を見て）その後（私は新しい種を見つける可能性が高いです）。

良い仮説文は、

• “if”と”then”の文を含めるべきである（カリフォルニア大学による）。
• 独立変数と従属変数の両方を含めます。
• 実験、調査、またはその他の科学的に健全な技術によってテスト可能であること。,
• 以前の研究の情報（あなたのものか他の人のものか）に基づいてください。
• い設計基準(工学またはプログラミング).li>

仮説検定とは何ですか？

統計における仮説検定は、調査または実験の結果をテストして、意味のある結果があるかどうかを確認する方法です。 だが基本試験かどうかの結果を有効によるコーヒーに飽きたら寿司に反する結果を行うことを目的として活動していチェックして下さい。, あなたの結果が偶然に起こったかもしれない場合、実験は反復可能ではないので、ほとんど使用されません。

仮説検定は、主にテストを実行する前に、帰無仮説が何であるかを知る必要があるため、学生にとって最も混乱する側面の一つになります。 しばしば、難しい言葉の問題がいることができる判読することは難しい., しかし、それはあなたが考えるよりも簡単です。

1. 帰無仮説を見つけ出し、
2. 帰無仮説を述べ、
3. 実行する必要があるテストの種類を選択し、
4. 帰無仮説をサポートまたは拒否します。
   1. 帰無仮説をサポートします。
   2. 帰無仮説をサポートするか、拒否します。li>

   帰無仮説とは何ですか？

   科学の歴史をさかのぼると、帰無仮説は常に受け入れられた事実です。 真であると一般に受け入れられている帰無仮説の簡単な例は次のとおりです。

   1. DNAは二重らせんのような形をしています。
      2. 太陽系には8つの惑星があります（冥王星を除く）。,
      3. Vioxxを服用すると、心臓の問題のリスクが高まります（薬は現在市場から取り出されています）。li>

      帰無仮説を述べるにはどうすればよいですか？

      基本的な統計で実際の実験や調査を実際に実行する必要はありません（あるいは”冥王星は惑星です”のような事実を反証することさえあり）、だからあなたは現実の状況から単語の問題を与えられるでしょう。 あなたはあなたの仮説が問題から何であるかを理解する必要があります。 これはちょうど受け入れられた事実がであるものを考え出すより少しトリッキーである場合 Wordの問題では、無効になる事実を見つけようとしています（すなわち, あなたが拒否できるもの）。

      仮説検定例#1:基本的な例

      研究者は、膝の手術患者が週二回（3回ではなく）理学療法に行くと、回復期間が長くなると考えています。 膝の外科患者のための平均回復時間は8.2週です。

      この質問の仮説文は、研究者が平均回復時間が8.2週間以上であると考えているということです。 数学用語では、
      H1:μ>8と書くことができます。,2

      次に、帰無仮説を述べる必要があります（帰無仮説を述べる方法を参照）。 それが研究者が間違っている場合に起こることです。 上記の例では、研究者が間違っている場合、回復時間は8.2週間以下です。 数学では、それは次のとおりです。
      H0≤8.2

      帰無仮説を拒否する

      十年前、太陽系には9つの惑星があると信じていました。 冥王星は2006年に惑星として降格されました。 “冥王星は惑星である”という帰無仮説は、”冥王星は惑星ではない”という帰無仮説に置き換えられました。,”もちろん、帰無仮説を拒否することは必ずしも簡単ではありません—難しい部分は、通常、あなたの帰無仮説が最初に何であるかを考え出すことです。

      仮説検定の例（一つのサンプルZ検定）

      一つのサンプルz検定はあまり頻繁に使用されません（実際の母集団標準偏差を知ることはめったに ただし、仮説検定で実行できる最も簡単なテストの一つであるため、それがどのように機能するかを理解することをお勧めします。, 英語のクラスでは、物語を書く前に（文法やスペルのような）基本を学ぶようになりました。 このページを含む二つの仮説検証の例が一つのサンプルz-試験までを実施。

      一つのサンプル仮説検定の例：＃2

      このビデオを見るために統計、マーケティングクッキーを受け入れてください。

      ある学校の校長は、彼の学校の学生が平均知性を上回っていると主張しています。 三十人の学生のIQスコアのランダムサンプルは112の平均スコアを持っています。, 校長の主張を支持するのに十分な証拠はありますか？ 平均母集団IQは100で、標準偏差は15です。

      ステップ1：帰無仮説を述べる。 受け入れられている事実は、母集団の平均が100であるため、H0：λ=100であるということです。

      ステップ2：代替仮説を述べる。 主張は、学生が平均IQスコアを上回っているということです。
      H1:√>100。
      ある点よりも”大きい”スコアを探しているということは、これが片側検定であることを意味します。

      ステップ3：問題を視覚化するのに役立つ画像を描画します。,
      

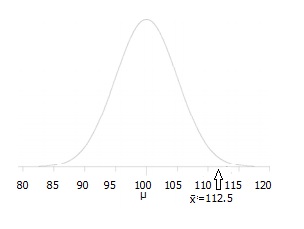
      ステップ4：アルファレベルを状態にします。 アルファレベルが与えられていない場合は、5％（0.05）を使用します。

      
      

      ステップ5：zテーブルから除去領域領域（上記のアルファレベルで与えられる）を見つけます。 のエリア。05はzスコア1.645に等しい。

      ステップ6：この式を使用して検定統計量を見つける：
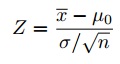
      このデータセットの場合：z= (112.5 – 100) / (15/√30) = 4.56.

      ステップ6：ステップ6がステップ5より大きい場合、帰無仮説を棄却します。, ステップ5より小さい場合、帰無仮説を棄却できません。 この場合、それはより大きい（4.56>1.645）ので、nullを拒否することができます。

      一つのサンプル仮説検定の例：＃3

      このビデオを見るために統計、マーケティングクッキーを受け入れてください。

      肥満患者の血糖値は平均100、標準偏差は15です。 研究者は、生のコーンスターチを多く含む食事は、血糖値に正または負の影響を及ぼすと考えています。, 未加工コーンスターチの食事療法を試みた30人の患者のサンプルに140の平均のブドウ糖のレベルがあります。 生のコーンスターチが効果を持っていたという仮説をテストします。 *TI-83またはExcelを使用してzスコア（”臨界値”）を計算すると、このプロセスがはるかに簡単になります。,
      参照：

      • 臨界z値TI83
      • ExcelのZスコア

      仮説検定の例：平均（TI83を使用）

      仮説検定にTI83計算機を使用することはできますが、仮説検定には

      問題の例：200人のサンプルの平均年齢は21で、母集団標準偏差（λ）は5です。 母集団平均が18.9であるという仮説をα=0.05で検定します。

      ステップ1：帰無仮説を述べる。, この場合、帰無仮説は母集団平均が18.9であるということであるため、
      H0:λ=18.9

      ステップ2:対立仮説を述べる。 21の代わりに18.9の平均を持つサンプルが実際に母集団と異なるかどうかを知りたいので、代替仮説：
      H1:≤18.9

      ステップ3：Statを押してから右矢印

      ステップ4：1を押して1：Z-Test….を選択します。 ENTERキーを押します。ステップ5：右矢印を使用して統計を選択します。

      ステップ6：問題のデータを入力します：φ0：18。,9
      ⌘:5
      x:21
      n:200
      ⌘:φ0

      ステップ7：下矢印を押して計算し、enterキーを押します。 電卓はp値を示しています：
      p=2.87×10-9

      これは私たちのアルファ値よりも小さいです。05. つまり、帰無仮説を棄却する必要があります。

      ベイズ仮説検定：それは何ですか？

      

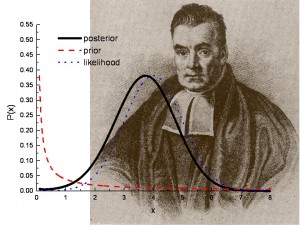
      画像：ロスアラモス国立研究所。

      ベイズ仮説検定は、質問に答えるのに役立ちます：テストまたは調査の結果を繰り返すことはできますか？
      テストを繰り返すことができるかどうかはなぜ気にしますか？, 同じ村の二十人が白血病で降りてきたとしましょう。 研究者のグループは、携帯電話の塔のせいであることがわかります。 しかし、第二の研究では、携帯電話の塔は村の癌クラスターとは何の関係もないことがわかりました。 実際、彼らは癌が完全にランダムであることを発見しました。 その音なので、実際にできる。 クラスターの癌できるようになるだけでチャンスです。 最初の研究が間違っていた理由はたくさんあるかもしれません。, 主な理由の一つは、彼らはちょうど時々事がランダムに起こると我々はちょうど理由がわからないことを考慮していないことができます。

      P値。

      あなたの研究結果が堅実であるかどうか、または偶然に起こった可能性があるかどうかを人々に知らせることは良い科学です。 これを行う通常の方法は、p値で結果をテストすることです。 P値は、データに対して仮説検定を実行することによって得られる数値です。 0.05（5％）以下のP値は、通常、結果が反復可能であると主張するのに十分です。, しかし、あなたの結果の妥当性をテストする別の方法があります：ベイズ仮説検定。 このタイプのテストはあなたの結果の強さをテストする別の方法を与える。

      ベイズ仮説検定。

      伝統的なテスト（おそらくelementary statsまたはAP statsで遭遇したタイプ）は非ベイズと呼ばれます。 それは結果が実験の繰り返された操業にどの位の割りで起こるかである。 それは実験が反復可能であるかどうかの客観的なビューです。
      ベイズ仮説検定は、同じことの主観的なビューです。, あなたの結果にどれだけの信仰があるかを考慮に入れます。 言い換えれば、あなたはあなたの実験の結果にお金を賭けるでしょうか？

      伝統的な仮説検定とベイズ仮説検定の違い。

      従来のテスト（非ベイズテスト）では、サンプリングを何度も繰り返す必要がありますが、ベイズテストではそうではありません。 二つの間の主な違いは、テストの最初のステップです：確率モデルを述べる。 ベイズテストでは、このステップに事前知識を追加します。, また、すべての証拠が考慮された後にランダムな事象に与えられる条件付き確率である事後確率を使用する必要があります。

      ベイズテストの引数。

      多くの研究者は、伝統的なテストに代わるものであると考えています。

      1. にはデータに関する事前知識が含まれているためです。
         2. 結果についての個人的な信念を考慮に入れます。

         に対する引数。

         1. 事前のデータや知識を含めることは正当ではありません。
         2. 非ベイズテストと比較して計算するのは難しいです。,

         トップに戻る

         仮説検定の記事

         基本：

         1. アドホックテストとは何ですか？
         2. 複合仮説検定
         3. 拒絶領域とは何ですか？li>
         4. 両側検定とは何ですか？
         5. 仮説検定が片側検定か両側検定かを判断する方法。
         6. 仮説が左側検定または右側検定であるかどうかを判断する方法。
         7. 帰無仮説を統計にどのように記述するか。li>
         8. どのように臨界値を見つけるために。
         9. 帰無仮説をサポートまたは拒否する方法。,

         特定のテスト：

         1. ANOVA。
         2. Brunner Munzel検定（一般化されたウィルコクソン検定）
         3. 正規性のカイ二乗検定
         4. Cochran-Mantel-Haenszel検定
         5. F検定
         6. グレンジャー因果関係テスト。
         7. ホテリングのT乗
         8. KPSSテスト。
         9. 尤度比検定とは何ですか？
         10. ログランクテスト。
         11. マンコバ
         12. シーケンシャル確率比テスト
         13. 符号テストを実行する方法。
         15. T検定：二つのサンプル。
         16. ウェルチのANOVA。
         17. 不等分散のためのウェルチのテスト。,
         18. Z-テスト：一つのサンプル。
         19. Zテスト：二割合
         20. ワルドテスト。
         1. 受け入れ領域とは何ですか？li>
         2. チェビシェフの定理を計算する方法。
         3. 決定ルール。
         4. 自由度。
         5. 方向テスト
         6. 偽発見率
         7. 最小有意差を計算する方法。
         8. 統計におけるレベル。
         9. エラーのマージンを計算する方法。li>
         10. 平均差（平均の違い）
         11. 複数のテストの問題を意味します。
         12. ネイマン-ピアソンの補題とは何ですか？
         13. 一つのサンプル中央値テスト。,
         14. REGWF
         15. サンプルサイズを見つける方法（一般的な手順）。
         16. 結果におけるSig2（尾付き）の意味
         17. 標準化された検定統計量とは何ですか？
         18. 標準エラーを見つける方法
         19. 標準化された値：例。li>
         20. どのようにTスコアを計算するか。
         22. 単一の平均をテストします。
         23. サンプルサイズが等しくない。
         24. 一様に最も強力なテスト。li>
         25. どのようにZスコアを計算するか。

         ——————————————————————————

         宿題やテストの質問に助けが必要ですか？, Chegg Studyを使用すると、その分野の専門家からあなたの質問に対するステップバイステップの解決策を得ることができます。 Cheggの家庭教師とのあなたの最初の30分は無料です！