- 歴史的背景
- 見かけの大きさ、m
- 絶対等級、M
- 星までの距離を求める-距離係数
- マグニチュード/距離計算
- 命名&星の識別
以下に示す星場写真を調べる。 これは、一般的にサザンクロスと呼ばれる、星座の核心の周りの空の領域を示しています。 移動カーソルの写真を一部です。
どの星が最も明るいですか?,

あなたはアルファ(α)ケンタウルス、写真の左下にある星を答えた場合は、あなたが正しいです。 ご覧のように、このような写真の画像は、肉眼で見ることができるよりも多くの星を示しています。 しかし一部の星が顕著になります。 Αケンタウリを選ぶ際には、いくつかの仮定をしました。 彼らは何でしたか?
このような写真は、より暗い星よりも大きな円盤として明るい星を示しています。, これは、これらの星が写真のより暗い星よりも物理的に大きいことを意味しますか? アストロメトリーのセクションでは、太陽以外のすべての星は非常に遠く、効果的に点源であることを学んだことを覚えておいてください。 なぜその一部が明るくなる(にち)以上の大きさ(写真)。 実際には明るさとは何ですか、それをどのように測定できますか? これらの質問に対する回答は、このセクションの焦点を形成します。,
歴史的背景

星の明るさを測定して比較するという概念は、ギリシャの天文学者で数学者のヒッパルコス(190-120BC)にまでさかのぼることができます。 古代の最も偉大な天文学者の一人、彼は位置と比較明るさを持つ850の星のカタログを作成すると信じられています。, 彼のシステムでは、最も明るい星は1の等級、次の最も明るい等級2など、肉眼で見える最も暗い星に6等級が割り当てられました。 この六点スケールは、ランキング、一流の星、最も明るい、最初の大きさであり、薄暗い低率の星は第六の大きさであったと考えることができます。
1600年代初頭に望遠鏡でより暗い星が発見されたため、規模を6等級を超えて拡張する必要がありました。, ジョン-ハーシェルらによる十九世紀における恒星の強度を測定するための視覚光度計の開発は、天文学者が国際標準を採用する必要性を促した。 1830年代にノーマン-ポグソンは、1等星の明るさが100×6等星の明るさよりも明るいことを提案した。 したがって、一つの大きさの差は、明るさの5÷100=2.512倍に等しかった。,
見かけの大きさm
星の見かけの大きさmは、地球上の観測者が見た大きさです。
太陽や月のような非常に明るい物体は、負の見かけの大きさを持つことができます。 ヒッパルコスはもともと明るい星を1等級と割り当てていたにもかかわらず、夜空で最も明るい星であるSiriusまたはΑ Canis Majoris(CMa)は実際にはm=-1.44の見かけの等級を持っていることを示しています。 ヒッパルコスの元の値の再調整により、明るい星ベガは見かけの等級が0.0であると定義されるようになった。,
1600年代初頭にかすかな星が望遠鏡で発見された後、マグニチュードスケールはマグニチュード6よりも暗い天体にも拡張されなければならなかった。 以下の表は、天体の見かけの大きさの範囲を示しています。
| オブジェクト | 見かけの 大きさ |
|---|---|
| 太陽 |
-26.5
|
| 満月 |
-12.5
|
| 金星 |
-4.,3
|
| Mars or Jupiter |
-2
|
| Sirius (α CMa) |
-1.44
|
| Vega (α Lyr) |
0.0
|
| Alnair (α Gru) |
1.73
|
| Naked-eye limit |
6.5
|
| Binocular limit |
10
|
| Proxima Cen |
11.,09
|
| Visual limit through 20 cm telescope |
14
|
| QSO at redshift z = 2 |
≈ 20
|
| Cepheid in galaxy M100 observed with HST |
26
|
| Galaxy at z = 6 observed with Gemini 8.1 m telescope |
28
|
| Limit for James Webb Space Telescope |
≥ 30
|
If a star of magnitude 1 is 2.,512×2等級の星よりも明るく、100&第六等級の星よりも明るい3等級の星よりもどれくらい明るいですか? ここでは気をつけてください。 それは単に2×2.512異なるものではありません。 あなたは一つの大きさの差が5÷100=2.512に等しいことを覚えておく必要があります。 したがって、2大きさの差=2.5122=6.31×明るさの差。
異なる大きさの二つのオブジェクトは、したがって、あなたの大きさの差の累乗に上げ2.512によって明るさが変化します。, これを式として書くと、大きさmAとmBを持つ二つのオブジェクトaとBの間の明るさまたは強度IA/IBの比は、次の式で与えられます。
例を見てみましょう。
例1:二つの星を比較します。
視等級+1.73のAlnairは、視等級11.09のProxima Cenよりもどれくらい明るいのでしょうか?
式4.1を使用して、私たちは持っています:
だから、代入:
例2:太陽は満月よりどれくらい明るいですか?
このために、上記の表から、太陽の見かけの等級は-26.5、満月は-12.5であることを思い出します。したがって、式4.1を使用すると、次のようになります。
代入すると、次のようになります。
絶対等級、M
シリウスの見かけの等級が-1.44で、ベテルギウスの見かけの等級が0.45であるという事実は、これら二つの星について何を教えてくれるのでしょうか? これについて考えるもう一つの方法は、なぜシリウスが夜空で最も明るい星であるのか尋ねることです。, P>
- それは本質的に明るいかもしれない、つまりそれは電磁放射の強力なエミッタであってもよいです、または
- それは私たちに非常に近いか、またはその両方であってもよいです。
したがって、星の見かけの大きさは、私たちからの距離に部分的に依存します。 実際、シリウスはベテルギウスよりも明るく見えますが、シリウスは私たちに非常に近く、わずか2.6pc離れていますが、ベテルギウスは約160pc離れています。, 星がすべて同じ光度を持つわけではないという認識は、見かけの大きさだけでは星を比較するのに十分ではないことを意味しました。 天文学者が星を直接比較できるようにする新しいシステムが開発されました。 このシステムは絶対等級Mと呼ばれます。
星の絶対等級Mは、星が私たちから10パーセクの距離にあった場合に持つであろう大きさです。 10pcの距離は純粋に恣意的ですが、今では天文学者によって国際的に合意されています。, 絶対等級のスケールは見かけの等級のスケールと同じであり、つまり1等級差=2.512倍の明るさの差です。 この対数スケールは、オープンエンドでユニットレスでもあります。 ここでも、Mの値が低いか負の値が多いほど、星は明るくなります。 絶対等級は、星の光度を表現する便利な方法です。 星の絶対等級が分かったら、他の星と比較することもできます。 ベテルギウス、M=-5.6は、本質的にM=1.41でシリウスよりも明るいです。
私たちの太陽は4.8の絶対視等級を持っています。,
星までの距離を求める-距離係数
あなたが天体測定のセクションから思い出すかもしれないように、ほとんどの星は視差を直接測定する それにもかかわらず、星の見かけの大きさと絶対の大きさの両方を知っていれば、その距離を決定できます。 シリウスとベテルギウスに加えて、GJ75と呼ばれる別の星をもう一度見てみましょう。
GJ75はどのくらい離れていますか? その見かけの大きさと絶対の大きさが同じであるという点で、これは珍しい星です。 どうして? その理由は、実際には私たちから10パーセク離れているため、定義により、その二つの大きさは同じでなければならないからです。,
シリウスはどうですか? その見かけの等級は、その絶対等級よりも低い(したがって明るい)。 これは、それが私たちに10パーセクよりも近いことを意味します。 ベテルギウスの見かけの等級は絶対等級よりも高い(したがって暗い)ので、10パーセクしか離れていなければ夜空でさらに明るく見えるでしょう。
天文学者は、星までの距離を表す方法として、見かけの等級と絶対等級の差である距離係数を使用します。
- 距離モジュラス=m-M
- 距離モジュラスは、10パーセクより近い星のために負です。,
- 距離モジュラスは、10パーセクよりも離れた星に対して正です。
- 距離係数のサイズは、距離の実際の値を決定するので、距離係数1.5の星は距離係数8.7の星よりも近くなります。
光度/距離の計算
距離係数は、次の式を使用して星までの距離を決定するために使用できます。
ここで、dはパーセク D=10pcの場合、mとMは同じであることに注意してください。 (この方程式の正式な導出は、光度に関する次のページで与えられている)。, NSW HSCシラバス式シートは、式を次のように提供します。
しかし、これは単に式4.2の再加工です。 するべきで快適に解決この式で与えられての変数. いくつかの例をどのように解決できるかを見てみましょう。
例3:Mとdを考えると、Mを見つける必要があります。
β Crucis(またはMimosa)は1.25の見かけの大きさを持ち、108パーセク離れています。 その絶対等級は何ですか?
式4.3を使用して、
したがって、β Crucisの絶対等級は-3.92
この計算は、各ステップが明示的になるように完全に機能することを示しています。 (振幅方程式を解く際に覚えておいてくださいlogは、自然対数またはlnではなく、10を底とする対数を指します。)
例4:MとMが与えられた場合、dを見つけます。
ベテルギウスの見かけの大きさは0.45、絶対等級は-5.14です。 どれくらい離れてる?
この問題では、式4.2を書き換えてdを未知のものとして与える必要があります。, これは以下に示されています:
今すぐ置き換えます:
したがって、ベテルギウスは約130pc離れています。
この例は、完全に作業が実現できない。, ただし、代数操作と置換を確認できるように、作業をこのような問題に明確に設定することが重要です。 作業ログを、指でトリッキーを知っていまからお電卓.
例5:Mとdを考えると、mを見つけます。
実際には、このタイプの問題は、通常は見かけの大きさを直接測定できるため、実際のオブジェクトにとってはあまり現実的ではありませんが、オブジェクトのクラスまたはタイプが他のパラメータを与えたかもしれない見かけの大きさを計算したい場合があります。 ここでも、式4から始まります。,3デネブのような絶対等級-8.73の超巨星が230パーセク離れていた場合、どれほど明るく現れるかを調べてみましょう。
したがって、次のように代入します。
したがって、Denebの見かけの大きさは-1.89になります。 これにより、夜空ではシリウス(m=-1.44)よりも明るくなります。, この値は大きな不確実性を持っていますが、実際にはDenebは約990pc遠いです。
例6:dが与えられていないが視差、pが与えられている場合はどうなりますか?
これは実際には非常にまっすぐ進んでいます。 距離と視差の間に直接的な関係があることを天体測定のセクションから思い出してください。
したがって、これを式4.2または4.3に挿入するだけです。
Naming&星を識別する
Cruxの写真とこのページの上部からのポインタを再訪してみましょう。, 下の写真は、著名な星がラベル付けされた同じ領域を示しています。 彼らはまた、見かけの大きさを示しています。 クラックスは、天球が天文学者によって国際的に分割され、合意された88の領域の一つである星座です。 Cruxは実際には星座の中で最も小さく、南の空で簡単に識別されます。 最近くの星が共通のポインタの実際の大きな星座と呼ばれCentaurus.

今、あなたは星がギリシャ語のアルファベットからの文字を使用して名前が付けられていることに気づくかもしれません。α、β、γ δおよびγ(アルファ、ベータ、ガンマ、デルタ、イプシロンが最初の五つである)に続いて、各星座の標準的な三文字の略語(CrucisまたはCruxのためのCruとケンタウルスのためのCen)。 クラックスの五つの星の見かけの大きさをよく見ると、最も明るい星はα、次のβなどとラベル付けされていることがわかります。, このシステムは1603年にそれを導入したヨハン-バイエルにちなんでバイエルシステムと呼ばれます。 星座の中で最も明るい星には、文字α、次のβなどが割り当てられます。 このルールの例外は、&alpha OrionisまたはBetelgeuseです。 実際にはβオリよりも暗く、少量でリゲルである。 これは、ベテルギウスがバイエルシステムの下で命名されて以来、明るさがわずかに薄暗くなっているという認識によって解決された興味深い歴史的,
星座について覚えておくべき点は、星座内の星は、星団の星とは異なり、通常、物理的に互いに関連付けられていないということです。 近くに一緒に見えるという事実は、純粋にツアーの視線に沿ったアライメント効果です。 実際には、上の領域の星は、次の画像に示すように、私たちから広く離れています。
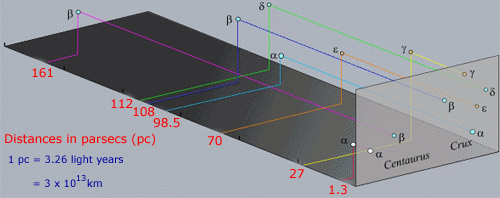
このようなα Cenのような明るい星のいくつかはまた、独自の固有の名前を持っています。 シリウス(α Sco)はそのような例の一つであり、α Cenはリゲル-ケンタウルスとも呼ばれる。 多くの星の名前は、ギリシャの記録がイスラムの天文学者によって保存され、開発された時代に由来するアラビア語です。 星の命名のバイエルシステムの問題は、ギリシャ語のアルファベットには24文字しかありませんが、各星座にあるよりも多くの星があることです。
ほとんどの星は、実際には特定の名前やバイエル分類を持っていません。, 最近の天文学者は、10万点以上の天体を持つ膨大な星のカタログをまとめているので、ほとんどの星はカタログ番号しか持っていません。 星は、それらが入っているカタログの数に応じて、複数の識別名またはカタログ番号を持つことができます。 たとえば、変光星δ Cepは、HIP110991、SAO34508、または30以上の他の識別子としても知られています。 多くのカタログは、天体を識別するために赤経や赤緯などの天体座標を利用しています。 したがって、δ CepはIRAS22273+5809、CCDM J22292+5825AおよびAAVSO2225+57として知られている。, カタログのRAとdecのわずかな変化は,星の固有運動と基準座標系の歳差運動によって生じる。