累積頻度
アーカイブされたコンテンツ
アーカイブされた情報は、参照、研究または記録 これは、カナダ政府のWeb標準の対象ではなく、アーカイブされてから変更または更新されていません。 利用可能な形式以外の形式をご希望の場合は、お問い合わせください。,
- 例1-離散変数
- 例2-連続変数
- その他の累積頻度計算
累積頻度は、データセット内の特定の値の上(または下)にある観測値の数を決定するために 累積頻度は、茎および葉のプロットから、またはデータから直接構築することができる頻度分布表を使用して計算されます。
累積頻度は、頻度分布表からの各周波数をその先行するものの合計に加算することによって計算されます。, すべての周波数がすでに前の合計に追加されているため、最後の値は常にすべての観測値の合計に等しくなります。
離散変数または連続変数
任意の計算における変数は、それらに割り当てられた値によって特徴付けることができます。 離散変数は、別々の不可分のカテゴリで構成されます。 変数とその近傍の間に値は存在できません。 たとえば、ある日から登録されているクラスの出席を観察すると、ある日に29人の学生がいて、別の日に30人の学生がいることがわかります。, ただし、学生の出席が29から30の間であることは不可能です。 (29人半の学生を持つ方法がないので、これら二つの値の間に値を観察する余地は単にありません。)
すべての変数が離散として特徴付けられるわけではありません。 いくつかの変数(時間、身長、体重など)は、不可分のカテゴリの固定されたセットに限定されません。 これらの変数は連続変数と呼ばれ、無限の数の可能な値に割り切れます。 例えば、時間は、時、分、秒、およびミリ秒の小数部で測定することができる。, したがって、11分または12分でレースを終えるのではなく、騎手と彼の馬は11分43秒でフィニッシュラインを通過することができます。
累積頻度を適切に計算するためには、二つのタイプの変数の違いを知ることが不可欠です。
例1-離散変数
アルバータ州レイクルイーズのロッククライマー数の合計は、30日間にわたって記録されました。 結果は次のとおりです。
31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56, 4, 54, 39, 52, 35, 51, 63, 42.,E離散変数へ:
- 茎と葉のプロットを設定します(茎と葉のプロットのセクションを参照)周波数、上位値、および累積頻度というラベルの追加の列を使用して
- 各茎の観測値の頻度を計算します
- 各茎の上限値を求めます
- 頻度列に数値を追加して累積頻度を計算します
回答:
- ロッククライマーの数は4から65の範囲です。 茎と葉のプロットを作成するには、データを10のクラス間隔でグループ化するのが最適です。
各間隔は、ステム列に配置することができます。 この列内の数値は、クラス間隔内の最初の数値を表します。 (たとえば、Stem0は間隔0-9を表し、Stem1は間隔10-19を表します。)
リーフ列には、各クラス区間内にある観測値の数がリストされます。, たとえば、Stem2(区間20-29)では、23、24、および26の三つの観測値は3、4、および6として表されます。
頻度列には、クラス区間内で見つかった観測値の数がリストされます。 例えば、茎5では九つの葉(または観察)が見つかり、茎1では二つの葉しか見つからなかった。
[Frequency]列を使用して累積頻度を計算します。
- まず、周波数カラムの番号を先行カラムに追加します。 たとえば、Stem0では、観測は一つしかなく、先行するものはありません。 累積頻度は一つです。,
1+0=1 - しかし、Stem1では二つの観測があります。 これら二つを前の累積頻度(一つ)に追加すると、結果は三つになります。
1+2=3 - Stem2では、三つの観測があります。 これらの三つを前の累積頻度(three)に追加し、合計(six)はStem2の累積頻度です。
3+3=6 - 周波数列のすべての数値を加算するまで、これらの計算を続けます。
- 結果を累積頻度列に記録します。,
[Upper value]列には、各クラス間隔で最も高い値を持つ観測値(変数)がリストされます。 たとえば、Stem1では、二つの観測値8と9は変数18と19を表します。 これら二つの変数の上限値は19です。
<キャプション>テーブル1.,>8 9
2 19 1 + 2 = 3 2 3 4 6 3 26 3 + 3 = 6 3 1 5 5 7 9 5 39 6 + 5 = 11 4 0 1 2 3 5 9 6 49 11 + 6 = 17 5 0 1 1 2 4 4 5 6 7 9 57 17 + 9 = 26 6 0 2 3 5 4 65 26 + 4 = 30 - まず、周波数カラムの番号を先行カラムに追加します。 たとえば、Stem0では、観測は一つしかなく、先行するものはありません。 累積頻度は一つです。,
- Since these variables are discrete, use the upper values in plotting the graph., ポイントをプロットして、ogiveと呼ばれる連続曲線を形成します。
グラフには、垂直軸上で行われた観測値の数に対応する累積頻度で常にラベルを付けます。,
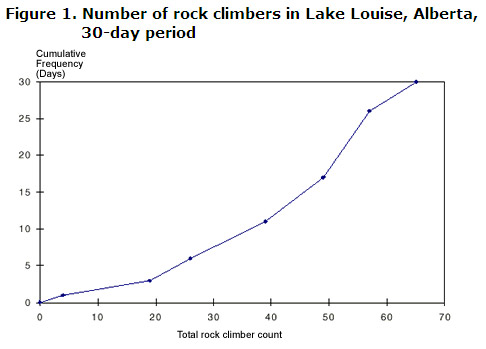
グラフまたはテーブルから次の情報を得ることができます。
- 11月30日に39人以下がレイクルイーズ周辺の岩を登った
- 13月30日に50人以上が岩を登った。around lake louise
連続変数を使用する場合、累積頻度の計算とグラフのプロットの両方に、離散変数に使用される方法とは若干異なるアプローチが必要です。,
例2-連続変数
紀元前ウィスラー山の雪の深さを25日間(最も近いセンチメートルまで)測定し、次のように記録しました。
242, 228, 217, 209, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257.,
- 上記の連続変数を使用して、次のことを行います。
- 頻度分布表の設定
- 各クラス間隔の頻度を見つける
- 各クラス間隔の終点を見つける
- 頻度列に数値を加えて累積頻度を計算する
- テーブルにすべての結果を記録する
- 頻度分布表から収集した情報を使用して累積頻度グラフをプロットします。
回答:
- 雪の深さの測定範囲は209cmから266cmです。, 頻度分布表を生成するために、データはそれぞれ10cmのクラス間隔でグループ化されるのが最善です。
積雪深欄には、10cmクラスの間隔が200cmから270cmまで記載されています。
頻度列には、特定の区間内にある観測値の数が記録されます。 この列は、集計の列の観測値を数値形式でのみ表します。,
エンドポイント列は、各観測値の実際の値にかかわらず、エンドポイントが区間の最大数であることを除いて、演習1の上位値列とよく似ています。 たとえば、210-220のクラス区間では、二つの観測値の実際の値は217と219です。 ただし、219を使用する代わりに、220のエンドポイントが使用されます。
累積頻度の列には、先行する周波数に追加された各周波数の合計がリストされます。
<キャプション>表2. ウィスラー山、B.C.で測定された雪の深さ,e2cd5a9″>
5 240 11 240 to < 250 
7 250 18 250 to < 260 
5 260 23 260 to < 270 
2 270 25 - Because the variable is continuous, the endpoints of each class interval are used in plotting the graph., プロットされたポイントは結合されてogiveを形成します。
図2に示すように、累積頻度(観測回数)は垂直y軸にラベル付けされ、その他の変数(積雪深)は水平x軸にラベル付けされます。,

グラフまたはテーブルから次の情報を得ることができます:
- 25日の雪の深さが200cm未満ではなかった
- 25日の雪の深さが210cm未満であった
- 25日の雪の深さが260cm以上であった
その他の累積頻度計算
頻度分布表を使用して得ることができるもう一つの計算は、相対頻度分布である。 このメソッドは、各クラス区間における観測値の割合として定義されます。, 相対累積頻度は、各区間の頻度を観測値の総数で割ることによって求めることができます。 (詳細については、”データの整理”の章の”頻度分布”を参照してください。)
度数分布表を使用して累積パーセンテージを計算することもできます。 この頻度分布の方法は、単なる頻度の割合とは対照的に、累積頻度の割合を与えます。