Test di Ipotesi
Lo scopo principale di statistiche è quello di verificare un’ipotesi. Ad esempio, potresti eseguire un esperimento e scoprire che un determinato farmaco è efficace nel trattamento del mal di testa. Ma se non puoi ripetere quell’esperimento, nessuno prenderà sul serio i tuoi risultati. Un buon esempio di ciò è stata la scoperta della fusione fredda, che si è ridotta nell’oscurità perché nessuno è stato in grado di duplicare i risultati.,
Guarda il video per una breve panoramica dei test di ipotesi, o continua a leggere qui sotto:
Contenuto (Clicca per saltare alla sezione):
- Che cos’è un’ipotesi?
- Che cos’è il test di ipotesi?
- Esempi di test di ipotesi (un campione Z Test).
- Test di ipotesi su una media (TI 83).
- Test di ipotesi bayesiana.
- Altri articoli di test di ipotesi
Vedi anche:
- Test di ipotesi in un’immagine
- Valori critici
- Qual è l’ipotesi Nulla?,
Hai bisogno di aiuto con un problema a casa? Controlla la nostra pagina di tutoraggio!
Che cos’è un’ipotesi?
Ipotesi di Andreas Cellarius, che mostra i moti planetari.
Un’ipotesi è un’ipotesi istruita su qualcosa nel mondo che ti circonda. Dovrebbe essere verificabile, mediante esperimento o osservazione. Ad esempio:
- Un nuovo farmaco che pensi possa funzionare.
- Un modo di insegnare si pensa potrebbe essere migliore.,
- Una possibile localizzazione di nuove specie.
- Un modo più equo per amministrare test standardizzati.
Può davvero essere qualsiasi cosa finché puoi metterlo alla prova.
Che cos’è una dichiarazione di ipotesi?
Se hai intenzione di proporre un’ipotesi, è consuetudine scrivere una dichiarazione. La tua dichiarazione sarà simile a questa:
“Se io…(fai questo su una variabile indipendente)….quindi (questo accadrà alla variabile dipendente).”
Per esempio:
- Se I (diminuire la quantità di acqua data alle erbe) quindi (le erbe aumenteranno di dimensioni).,
- Se io (dare ai pazienti consulenza in aggiunta ai farmaci) poi (la loro scala di depressione complessiva diminuirà).
- Se io (dare esami a mezzogiorno invece di 7) poi (punteggi dei test degli studenti miglioreranno).
- Se io (guardo in questa determinata posizione) allora (sono più propenso a trovare nuove specie).
Una buona affermazione di ipotesi dovrebbe:
- Includere una dichiarazione “if” e “then” (secondo l’Università della California).
- Include sia le variabili indipendenti che quelle dipendenti.
- Essere testabile da esperimento, indagine o altra tecnica scientificamente suono.,
- Essere basato su informazioni nella ricerca precedente (sia il vostro o di qualcun altro).
- Hanno criteri di progettazione (per progetti di ingegneria o di programmazione).
Che cos’è il test di ipotesi?
Il test di ipotesi nelle statistiche è un modo per testare i risultati di un sondaggio o di un esperimento per vedere se si hanno risultati significativi. Stai fondamentalmente testando se i tuoi risultati sono validi per capire le probabilità che i tuoi risultati siano accaduti per caso., Se i tuoi risultati potrebbero essere accaduti per caso, l’esperimento non sarà ripetibile e quindi ha poco uso.
Il test di ipotesi può essere uno degli aspetti più confusi per gli studenti, soprattutto perché prima di poter eseguire un test, devi sapere qual è la tua ipotesi nulla. Spesso, quei problemi di parole difficili che si trovano ad affrontare possono essere difficili da decifrare., Ma è più facile di quanto pensi; tutto quello che devi fare è:
- Capire la tua ipotesi nulla,
- Dichiarare la tua ipotesi nulla,
- Scegliere che tipo di test è necessario eseguire,
- Supportare o rifiutare l’ipotesi nulla.
Qual è l’ipotesi Nulla?
Se si ripercorre la storia della scienza, l’ipotesi nulla è sempre il fatto accettato. Semplici esempi di ipotesi nulle che sono generalmente accettate come vere sono:
- Il DNA ha la forma di una doppia elica.
- Ci sono 8 pianeti nel sistema solare (escluso Plutone).,
- L’assunzione di Vioxx può aumentare il rischio di problemi cardiaci (un farmaco ora tolto dal mercato).
Come faccio a dichiarare l’ipotesi Nulla?
Non ti verrà richiesto di eseguire effettivamente un vero esperimento o un sondaggio nelle statistiche elementari (o addirittura confutare un fatto come “Plutone è un pianeta”!), quindi ti verranno dati problemi di parole da situazioni di vita reale. Avrai bisogno di capire quale sia la tua ipotesi dal problema. Questo può essere un po ‘ più complicato del semplice capire quale sia il fatto accettato. Con i problemi di word, stai cercando di trovare un fatto che è nullificabile (cioè, qualcosa che puoi rifiutare).
Esempi di test di ipotesi #1: Esempio di base
Un ricercatore pensa che se i pazienti con chirurgia del ginocchio vanno in terapia fisica due volte a settimana (invece di 3 volte), il loro periodo di recupero sarà più lungo. I tempi medi di recupero per i pazienti con chirurgia del ginocchio sono di 8,2 settimane.
L’affermazione di ipotesi in questa domanda è che il ricercatore ritiene che il tempo medio di recupero sia superiore a 8,2 settimane. Può essere scritto in termini matematici come:
H1: μ > 8.,2
Successivamente, dovrai dichiarare l’ipotesi nulla (Vedi: Come dichiarare l’ipotesi nulla). Questo è ciò che accadrà se il ricercatore ha torto. Nell’esempio precedente, se il ricercatore ha torto, il tempo di recupero è inferiore o uguale a 8,2 settimane. In matematica, questo è:
H0 μ ≤ 8.2
Rifiutando l’ipotesi nulla
Dieci anni fa, credevamo che ci fossero 9 pianeti nel sistema solare. Plutone è stato retrocesso come pianeta nel 2006. L’ipotesi nulla di ” Plutone è un pianeta “è stata sostituita da” Plutone non è un pianeta.,”Naturalmente, rifiutare l’ipotesi nulla non è sempre così facile—la parte difficile è di solito capire quale sia la tua ipotesi nulla in primo luogo.
Esempi di test di ipotesi (One Sample Z Test)
Il test one sample z non viene utilizzato molto spesso (perché raramente conosciamo la deviazione standard effettiva della popolazione). Tuttavia, è una buona idea capire come funziona in quanto è uno dei test più semplici che è possibile eseguire nei test di ipotesi., Nella classe di inglese devi imparare le basi (come la grammatica e l’ortografia) prima di poter scrivere una storia; pensa a un campione di test z come base per comprendere test di ipotesi più complessi. Questa pagina contiene due esempi di test di ipotesi per un campione z-test.
Un esempio di test di ipotesi Esempi: #2
Un preside di una certa scuola afferma che gli studenti della sua scuola sono al di sopra dell’intelligenza media. Un campione casuale di trenta studenti IQ punteggi hanno un punteggio medio di 112., Ci sono prove sufficienti per sostenere la richiesta del preside? Il QI medio della popolazione è 100 con una deviazione standard di 15.
Passaggio 1: Indicare l’ipotesi Nulla. Il fatto accettato è che la media della popolazione è 100, quindi: H0: μ=100.
Passaggio 2: Indicare l’ipotesi alternativa. L’affermazione è che gli studenti hanno punteggi IQ superiori alla media, quindi:
H1: μ > 100.
Il fatto che stiamo cercando punteggi “maggiori di” un certo punto significa che questo è un test a una coda.
Passo 3: Disegna un’immagine per aiutarti a visualizzare il problema.,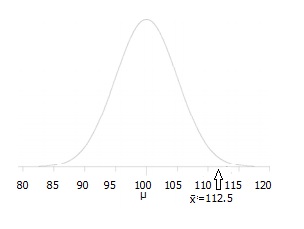
Passo 4: Indicare il livello alfa. Se non ti viene dato un livello alfa, usa 5% (0,05).
Passo 5: Trova l’area della regione di rifiuto (data dal tuo livello alfa sopra) dalla tabella z. Un’area di .05 è uguale a un punteggio z di 1.645.
Passo 6: Trova la statistica del test usando questa formula: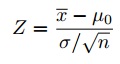 
Per questo set di dati: z= (112.5 – 100) / (15/√30) = 4.56.
Passaggio 6: se il passaggio 6 è maggiore del passaggio 5, rifiutare l’ipotesi nulla., Se è inferiore al passaggio 5, non è possibile rifiutare l’ipotesi nulla. In questo caso, è maggiore (4.56 > 1.645), quindi puoi rifiutare il null.
Un esempio di test di ipotesi Esempi: #3
I livelli di glucosio nel sangue per i pazienti obesi hanno una media di 100 con una deviazione standard di 15. Un ricercatore pensa che una dieta ricca di amido di mais crudo avrà un effetto positivo o negativo sui livelli di glucosio nel sangue., Un campione di 30 pazienti che hanno provato la dieta di amido di mais crudo ha un livello medio di glucosio di 140. Prova l’ipotesi che l’amido di mais crudo abbia avuto un effetto.
* Questo processo è reso molto più semplice se si utilizza un TI-83 o Excel per calcolare il punteggio z (il”valore critico”).,
Vedi:
- Valore z critico TI 83
- Punteggio Z in Excel
Esempi di test di ipotesi: Media (usando TI 83)
Puoi usare la calcolatrice TI 83 per il test di ipotesi, ma la calcolatrice non capirà le ipotesi nulle e alternative; sta a te leggere la domanda e inserirla nella calcolatrice.
Problema di esempio: un campione di 200 persone ha un’età media di 21 anni con una deviazione standard della popolazione (σ) di 5. Prova l’ipotesi che la media della popolazione sia 18,9 a α = 0,05.
Passaggio 1: Indicare l’ipotesi nulla., In questo caso, l’ipotesi nulla è che la media della popolazione sia 18.9, quindi scriviamo:
H0: μ = 18.9
Passaggio 2: Indicare l’ipotesi alternativa. Vogliamo sapere se il nostro campione, che ha una media di 21 invece di 18.9, è davvero diverso dalla popolazione, quindi la nostra ipotesi alternativa:
H1: μ 1 18.9
Passo 3: Premere Stat quindi premere due volte la freccia destra per selezionare i TEST.
Passo 4: Premere 1 per selezionare 1: Z-Test…. Premere INVIO.
Passo 5: Usa la freccia destra per selezionare le statistiche.
Passo 6: Inserire i dati dal problema:
μ0: 18.,9
σ: 5
x: 21
n: 200
μ: μ μ0
Passo 7: Freccia verso il basso per calcolare e premere INVIO. La calcolatrice mostra il valore p:
p = 2,87 × 10-9
Questo è più piccolo del nostro valore alfa di .05. Ciò significa che dovremmo respingere l’ipotesi nulla.
Test di ipotesi bayesiana: che cos’è?
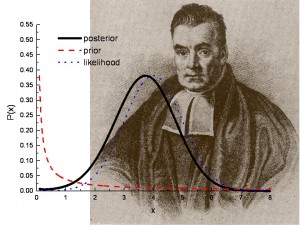
Immagine: Los Alamos National Lab.
Il test di ipotesi bayesiana aiuta a rispondere alla domanda: i risultati di un test o di un sondaggio possono essere ripetuti?
Perché ci interessa se un test può essere ripetuto?, Diciamo che venti persone nello stesso villaggio sono venute con la leucemia. Un gruppo di ricercatori scopre che le torri dei telefoni cellulari sono da biasimare. Tuttavia, un secondo studio ha rilevato che le torri dei telefoni cellulari non avevano nulla a che fare con il cluster del cancro nel villaggio. In effetti, hanno scoperto che i tumori erano completamente casuali. Se questo sembra impossibile, in realtà può accadere! I cluster di cancro possono accadere semplicemente per caso. Ci potrebbero essere molte ragioni per cui il primo studio era difettoso., Uno dei motivi principali potrebbe essere che non hanno tenuto conto del fatto che a volte le cose accadono casualmente e non sappiamo perché.
Valori P.
È una buona scienza far sapere se i risultati dello studio sono solidi o se potrebbero essere accaduti per caso. Il solito modo di farlo è testare i risultati con un valore P. Un valore p è un numero che si ottiene eseguendo un test di ipotesi sui dati. Un valore P di 0,05 (5%) o inferiore è di solito sufficiente per affermare che i risultati sono ripetibili., Tuttavia, c’è un altro modo per testare la validità dei risultati: test di ipotesi bayesiana. Questo tipo di test ti offre un altro modo per testare la forza dei tuoi risultati.
Test di ipotesi bayesiana.
I test tradizionali (il tipo che probabilmente hai incontrato nelle statistiche elementari o nelle statistiche AP) sono chiamati Non bayesiani. È la frequenza con cui un risultato si verifica su ripetute esecuzioni dell’esperimento. È una visione oggettiva se un esperimento è ripetibile.
Il test di ipotesi bayesiana è una visione soggettiva della stessa cosa., Prende in considerazione quanta fede hai nei tuoi risultati. In altre parole, scommetteresti denaro sull’esito del tuo esperimento?
Differenze tra test di ipotesi tradizionale e bayesiana.
Il test tradizionale (non bayesiano) richiede di ripetere il campionamento più e più volte, mentre il test bayesiano no. La principale differenza tra i due è nella prima fase del test: indicare un modello di probabilità. Nei test bayesiani si aggiungono conoscenze precedenti a questo passaggio., Richiede anche l’uso di una probabilità posteriore, che è la probabilità condizionale data a un evento casuale dopo che tutte le prove sono state considerate.
Argomenti per il test bayesiano.
Molti ricercatori pensano che sia un’alternativa migliore ai test tradizionali, perché:
- Include una conoscenza preliminare dei dati.
- Tiene conto delle convinzioni personali sui risultati.
Argomenti contro.
- Includere dati o conoscenze precedenti non è giustificabile.
- È difficile da calcolare rispetto ai test non bayesiani.,
Torna all’inizio
Articoli per il test di ipotesi
Nozioni di base:
- Che cos’è il test ad Hoc?
- Test di ipotesi composita
- Che cos’è una regione di rifiuto?
- Che cos’è un test a due code?
- Come decidere se un test di ipotesi è un test a una coda o un test a due code.
- Come decidere se un’ipotesi è un test a coda sinistra o un test a coda destra.
- Come dichiarare l’ipotesi nulla nelle statistiche.
- Come trovare un valore critico.
- Come supportare o rifiutare un’ipotesi Nulla.,
Test specifici:
- ANOVA.
- Test di Brunner Munzel (Test di Wilcoxon generalizzato)
- Test Chi Quadrato per la normalità
- Test di Cochran-Mantel-Haenszel
- Test F
- Test di causalità Granger.
- T-Squared di Hotelling
- Test KPSS.
- Che cos’è un test del rapporto di verosimiglianza?
- Log rank test.
- MANCOVA
- Sequential Probability Ratio Test
- Come eseguire un test segno.
- T Test: un campione.
- T-Test: due campioni.
- ANOVA di Welch.
- Test di Welch per varianze disuguali.,
- Z-Test: un campione.
- Z Test: Due proporzione
- Wald Test.
- Che cos’è una regione di accettazione?
- Come calcolare il teorema di Chebyshev.
- Regola di decisione.
- Gradi di libertà.
- Test direzionale
- False Discovery Rate
- Come calcolare la differenza meno significativa.
- Livelli nelle statistiche.
- Come calcolare il margine di errore.
- Differenza media (Differenza di mezzi)
- Il problema di test multipli.
- Qual è il lemma di Neyman-Pearson?
- Una prova mediana del campione.,
- REGWF
- Come trovare una dimensione del campione (istruzioni generali).
- Sig 2 (Tailed) significato nei risultati
- Cos’è una statistica di test standardizzata?
- Come trovare l’errore standard
- Valori standardizzati: Esempio.
- Come calcolare un T-Score.
- T-Score Vs. a Z. Score.
- Testare una singola media.
- Dimensioni del campione disuguali.
- Test uniformemente più potenti.
- Come calcolare un punteggio Z.
——————————————————————————
Hai bisogno di aiuto con un compito a casa o una domanda di prova?, Con Chegg Studio, è possibile ottenere soluzioni passo-passo alle vostre domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!