- Sfondo Storico
- Magnitudine Apparente, m
- Magnitudine Assoluta, M
- Trovare la Distanza delle Stelle – Modulo di Distanza
- Grandezza/Distanza Calcoli
- Denominazione & Identificazione di Stelle
Studiare il campo della stella fotografia mostrato di seguito. Mostra una regione del cielo attorno alla costellazione Crux, comunemente chiamata Croce del Sud. Spostare il cursore sulla foto per identificare alcune stelle.
Quale stella è più luminosa?,

Se hai risposto Alpha (α) Centauri, la stella in basso a sinistra della fotografia hai ragione. Come puoi vedere, un’immagine fotografica come questa mostra molte più stelle di quante tu possa vedere ad occhio nudo. Tuttavia alcune stelle sono più prominenti di altre. Nella scelta di α Centauri hai fatto alcune ipotesi. Cosa erano?
Una fotografia come questa mostra stelle luminose come dischi più grandi di stelle più deboli., Questo significa che queste stelle sono fisicamente più grandi delle stelle più deboli nella foto? Ricorda, nella sezione sull’astrometria abbiamo imparato che tutte le stelle diverse dal nostro Sole sono così distanti che sono effettivamente fonti puntiformi. Perché allora alcuni appaiono più luminosi (ai nostri occhi) o più grandi (nelle fotografie) di altri? Cos’è, infatti, la luminosità e come possiamo misurarla? Le risposte a queste domande formano il focus di questa sezione.,
Background storico

Il concetto di misurazione e confronto della luminosità delle stelle può essere fatto risalire all’astronomo e matematico greco Ipparco (190 – 120 AC). Uno dei più grandi astronomi dell’antichità, è accreditato di aver prodotto un catalogo di 850 stelle con posizioni e luminosità comparative., Nel suo sistema, alle stelle più luminose è stata assegnata una magnitudine di 1, la successiva magnitudine più luminosa 2 e così via alle stelle più deboli, appena visibili ad occhio nudo che erano magnitudine 6. Questa scala a sei punti può essere pensato come una classifica, stelle di prim’ordine, il più luminoso, erano prima magnitudine e dim stelle a basso tasso erano sesta magnitudine.
La scoperta di stelle più deboli con i telescopi nei primi anni del 1600 richiese che la scala fosse estesa oltre la magnitudine 6., Lo sviluppo di fotometri visivi, strumenti per misurare le intensità stellari, nel diciannovesimo secolo da John Herschel e altri ha spinto la necessità per gli astronomi di adottare uno standard internazionale. Il fatto che gli occhi rilevino differenze di intensità logaritmicamente piuttosto che linearmente fu scoperto nel 1830. Nel 1856 Norman Pogson propose che una stella di magnitudine 1 fosse 100 × più luminosa di una stella di magnitudine 6. Una differenza di una magnitudine era quindi pari a 5√100 = 2.512 volte in luminosità.,
Magnitudine apparente, m
La magnitudine apparente, m, di una stella è la magnitudine che ha visto da un osservatore sulla Terra.
Un oggetto molto luminoso, come il Sole o la Luna può avere una magnitudine apparente negativa. Anche se Ipparco originariamente assegnava alle stelle più luminose una magnitudine di 1, un confronto più attento mostra che la stella più luminosa del cielo notturno, Sirio o α Canis Majoris (CMa) ha in realtà una magnitudine apparente di m = -1,44. Con la ricalibrazione dei valori originali di Ipparco la stella luminosa Vega è ora definita per avere una magnitudine apparente di 0,0.,
In seguito alla scoperta telescopica di stelle deboli nei primi anni del 1600, la scala di magnitudine ha dovuto essere estesa anche a oggetti più deboli di magnitudine 6. La tabella seguente mostra la gamma di magnitudini apparenti per gli oggetti celesti.
| Oggetto | Apparente Magnitudine |
|---|---|
| Sole |
-26.5
|
| Luna Piena |
-12.5
|
| Venere |
-4.,3
|
| Mars or Jupiter |
-2
|
| Sirius (α CMa) |
-1.44
|
| Vega (α Lyr) |
0.0
|
| Alnair (α Gru) |
1.73
|
| Naked-eye limit |
6.5
|
| Binocular limit |
10
|
| Proxima Cen |
11.,09
|
| Visual limit through 20 cm telescope |
14
|
| QSO at redshift z = 2 |
≈ 20
|
| Cepheid in galaxy M100 observed with HST |
26
|
| Galaxy at z = 6 observed with Gemini 8.1 m telescope |
28
|
| Limit for James Webb Space Telescope |
≥ 30
|
If a star of magnitude 1 is 2.,512 × più luminosa di una stella di magnitudine 2 e 100 & volte più luminosa di una stella di sesta magnitudine quanto è più luminosa di una stella di magnitudine 3? Devi stare attento qui. Non è semplicemente 2 × 2.512 diverso. È necessario ricordare che una differenza di una grandezza è uguale a 5√100 = 2.512. Una differenza di 2 magnitudini quindi = 2.5122 = 6.31 × differenza di luminosità.
Due oggetti di diversa magnitudine quindi variano in luminosità di 2.512 elevato alla potenza della differenza di magnitudine., Se scriviamo questo come un’equazione, il rapporto tra luminosità o intensità, IA / IB tra due oggetti, A e B, con magnitudini mA e mB è dato dalla seguente equazione:
Diamo un’occhiata a un esempio.
Esempio 1: Confronto tra due stelle.
Quanto più luminoso è Alnair, magnitudine apparente di +1,73 rispetto a Proxima Cen con una magnitudine di 11,09?
Usando l’equazione 4.1 abbiamo:
quindi, sostituendo in:
Esempio 2: Quanto più luminoso è il Sole della Luna piena?
Per questo ricordiamo dalla tabella sopra che il Sole ha una magnitudine apparente di -26,5 e la Luna piena, – 12,5.
Quindi usando l’equazione 4.1 otteniamo:
sostituendo in ci dà:
È importante ricordare che la grandezza è semplicemente un numero, non ha unità. Il simbolo per la magnitudine apparente è un minuscolo m; è necessario chiarire questo in qualsiasi problema.
Magnitudine assoluta, M
Cosa ci dice il fatto che Sirio abbia una magnitudine apparente di -1,44 e Betelgeuse una magnitudine apparente di 0,45 su queste due stelle? Un altro modo di pensare a questo è chiedere perché Sirius è la stella più luminosa del cielo notturno?, Una stella può apparire luminosa per due motivi principali:
- Può essere intrinsecamente luminosa, cioè può essere un potente emettitore di radiazioni elettromagnetiche, o
- Può essere molto vicina a noi, o entrambi.
La magnitudine apparente di una stella dipende quindi in parte dalla sua distanza da noi. In effetti Sirius appare più luminoso di Betelgeuse proprio perché Sirius è molto vicino a noi, a soli 2,6 pc di distanza mentre Betelgeuse è a circa 160 pc di distanza., La consapevolezza che le stelle non hanno tutte la stessa luminosità significava che la sola magnitudine apparente non era sufficiente per confrontare le stelle. È stato sviluppato un nuovo sistema che consentirebbe agli astronomi di confrontare direttamente le stelle. Questo sistema è chiamato la magnitudine assoluta, M.
La magnitudine assoluta, M, di una stella è la magnitudine che la stella avrebbe se fosse ad una distanza di 10 parsec da noi. Una distanza di 10 pc è puramente arbitraria ma ora concordata a livello internazionale dagli astronomi., La scala per la magnitudine assoluta è la stessa di quella per la magnitudine apparente, cioè una differenza di 1 magnitudine = 2,512 volte la differenza di luminosità. Questa scala logaritmica è anche aperta e senza unità. Ancora una volta, più basso o più negativo è il valore di M, più luminosa è la stella. La magnitudine assoluta è un modo conveniente per esprimere la luminosità di una stella. Una volta conosciuta la magnitudine assoluta di una stella, puoi anche confrontarla con altre stelle. Betelgeuse, M = -5.6 è intrinsecamente più luminoso di Sirius con un M = 1.41.
Il nostro Sole ha una magnitudine visiva assoluta di 4,8.,
Trovare la distanza dalle stelle – Modulo della distanza
Come si può ricordare dalla sezione sull’astrometria, la maggior parte delle stelle sono troppo distanti per avere la loro parallasse misurata direttamente. Tuttavia, se si conoscono sia le magnitudini apparenti che assolute per una stella, è possibile determinare la sua distanza. Guardiamo ancora Sirius e Betelgeuse più un’altra stella chiamata GJ 75.
Quanto dista GJ 75? È una stella insolita in quanto le sue magnitudini apparenti e assolute sono le stesse. Perché? Il motivo è che in realtà è distante 10 parsec da noi, quindi per definizione le sue due grandezze devono essere le stesse.,
Che dire di Sirius? La sua magnitudine apparente è inferiore (quindi più luminosa) rispetto alla sua magnitudine assoluta. Ciò significa che è più vicino di 10 parsec a noi. La magnitudine apparente di Betelgeuse è più alta (quindi più debole) della sua magnitudine assoluta, quindi sembrerebbe ancora più luminosa nel cielo notturno se fosse distante solo 10 parsec.
Gli astronomi usano la differenza tra magnitudine apparente e assoluta, il modulo di distanza, come un modo per de terminare la distanza da una stella.
- Modulo di distanza = m – M.
- Modulo di distanza è negativo per le stelle più vicine di 10 parsec.,
- Modulo di distanza è positivo per le stelle più lontano di 10 parsec.
- La dimensione del modulo di distanza determina il valore effettivo della distanza, in modo che una stella di modulo di distanza 1.5 sia più vicina di una con un modulo di distanza di 8.7.
Calcoli di magnitudine/Distanza
Il modulo di distanza può essere usato per determinare la distanza da una stella usando l’equazione:
dove d è in parsec. Si noti che se d = 10 pc, m e M sono uguali. (Una derivazione formale di questa equazione è data nella pagina successiva sulla luminosità)., Il foglio formula NSW HSC Syllabus fornisce l’equazione come:
ma questa è semplicemente una rielaborazione dell’equazione 4.2. Dovresti essere a tuo agio nel risolvere questa equazione date due delle tre variabili. Fateci sapere guardare come si può risolvere alcuni esempi.
Esempio 3: Dato m e d, è necessario trovare M.
β Crucis (o Mimosa) ha una magnitudine apparente di 1,25 ed è distante 108 parsec. Qual è la sua grandezza assoluta?
Usando l’equazione 4.3 abbiamo:
quindi β Crucis ha una magnitudine assoluta di -3.92
Nota questo calcolo ha mostrato il pieno funzionamento in modo che ogni passo sia esplicito. (Ricorda che nel risolvere le equazioni di magnitudine il log si riferisce ai logaritmi in base 10 e non ai logaritmi naturali o ln.)
Esempio 4: Dato M e M, trova d.
Betelgeuse ha una magnitudine apparente di 0,45 e una magnitudine assoluta di -5,14. Quanto è lontano?
Questo problema ci richiede di riscrivere l’equazione 4.2 per darci d come sconosciuto., Questo è illustrato di seguito:
che può essere scritto come:
ora che sostituisce in:
Betelgeuse è di circa 130 pc distanti.
Ancora una volta, questo esempio mostra il funzionamento completo mentre in realtà non puoi mostrare ogni passo., È importante, tuttavia, impostare chiaramente il lavoro su tali problemi in modo da poter controllare la manipolazione algebrica e le sostituzioni. Lavorare con i registri e gli indici può essere difficile in modo da assicurarsi di sapere come fare questi sulla calcolatrice.
Esempio 5: Dato M e d, trova m.
In pratica questo tipo di problema è meno realistico per gli oggetti reali poiché normalmente possiamo misurare direttamente le loro magnitudini apparenti, tuttavia potrebbe essere che desideriamo calcolare quale magnitudine apparente una classe o un tipo di oggetto può aver dato gli altri parametri. Ancora una volta, a partire dall’equazione 4.,3 determiniamo quanto apparirebbe brillante una supergigante come Deneb con una magnitudine assoluta di -8,73 se fosse a 230 parsec di distanza.
quindi, sostituendo:
Deneb sarebbe una magnitudine apparente di -1.89. Ciò lo renderebbe più luminoso nel nostro cielo notturno di Sirius (m = -1.44)., In realtà Deneb è distante circa 990 pc anche se questo valore ha una grande incertezza.
Esempio 6: Cosa succede se d non è dato ma parallax, p è dato?
Questo è in realtà molto semplice. Ricordiamo dalla sezione sull’astrometria che esiste una relazione diretta tra distanza e parallasse.
quindi devi semplicemente inserire questo nell’equazione 4.2 o 4.3.
Denominazione& Identificazione delle stelle
Facci sapere rivisita quella foto di Crux e i Puntatori dall’alto di questa pagina., La foto qui sotto mostra la stessa regione con le stelle prominenti etichettate. Hanno anche mostrato le loro magnitudini apparenti. Crux è una costellazione, una delle 88 regioni in cui la sfera celeste è stata suddivisa e concordata a livello internazionale dagli astronomi. Crux è in realtà la più piccola delle costellazioni ed è facilmente identificabile nei cieli meridionali. Le prominenti stelle vicine comunemente chiamate Puntatori sono in realtà parte di una grande costellazione chiamata Centaurus.

Ora puoi notare che le stelle sono denominate usando lettere dell’alfabeto greco; α, β, γ δ e ε (alfa, beta, gamma, delta, epsilon sono le prime cinque) seguite dall’abbreviazione standard di tre lettere per ogni costellazione (Cru per Crucis o Crux e Cen per Centaurus). Se osservi attentamente le magnitudini apparenti per le cinque stelle nominate in Crux vedrai che la stella più luminosa è etichettata α, la successiva β e così via., Questo sistema è chiamato sistema Bayer, dopo Johann Bayer che lo introdusse nel 1603. Alla stella più luminosa di una costellazione viene assegnata la lettera α, la successiva β e così via. Un’eccezione a questa regola è & alpha Orionis o Betelgeuse. È infatti più debole di β Ori, Rigel di una piccola quantità. Questo è un caso storico interessante risolto dalla realizzazione che Betelgeuse ha oscurato leggermente in luminosità da quando è stato nominato sotto il sistema Bayer.,
Un punto da ricordare sulle costellazioni è che le stelle all’interno di una costellazione di solito non sono fisicamente associate tra loro, a differenza delle stelle negli ammassi. Il fatto che appaiono vicini è puramente un effetto di allineamento lungo la linea di vista del tour. In effetti, le stelle nella regione sopra sono ampiamente separate in distanza da noi come mostrato nell’immagine successiva.
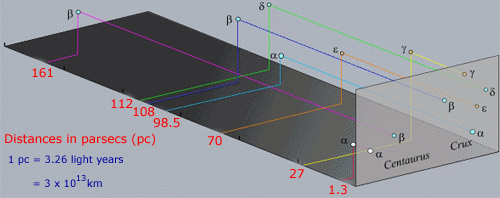
Alcune delle stelle luminose come α Cen hanno anche il loro nome specifico. Sirius (α Sco) è uno di questi esempi mentre α Cen è anche chiamato Rigel Kentaurus. Molti nomi di stelle sono di origine araba dall’epoca in cui i record greci sono stati conservati e sviluppati dagli astronomi islamici. Il problema con il sistema Bayer di nominare le stelle è che ci sono solo 24 lettere nell’alfabeto greco, ma ci sono molte più stelle di quante ce ne siano in ogni costellazione.
La maggior parte delle stelle infatti non ha un nome specifico o una classificazione Bayer., In questi giorni gli astronomi hanno compilato vasti cataloghi di stelle, alcune con oltre 10 milioni di oggetti, quindi la maggior parte delle stelle ha solo un numero di catalogo. Le stelle possono avere più di un nome di identificazione o un numero di catalogo, a seconda del numero di cataloghi in cui si trovano. La stella variabile, δ Cep per esempio è anche conosciuta come HIP 110991, SAO 34508, o uno qualsiasi di più di 30 altri identificatori! Molti cataloghi utilizzano coordinate celesti come Ascensione retta e Declinazione per identificare gli oggetti. Così δ Cep è conosciuto come IRAS 22273 + 5809, CCDM J22292 + 5825A e AAVSO 2225 + 57., Le leggere variazioni di RA e dec per i cataloghi derivano dal moto corretto delle stelle e dalla precessione del quadro di riferimento.