kumulatív frekvencia

• 1. példa – diszkrét változók
• 2. példa-folyamatos változók
• Egyéb kumulatív frekvencia számítások

kumulatív frekvencia az adatkészletben egy adott érték felett (vagy alatt) lévő megfigyelések számának meghatározására szolgál. A halmozott frekvenciát egy frekvenciaelosztási táblázat segítségével számítjuk ki, amely a szárból és a levelekből, vagy közvetlenül az adatokból építhető ki.

a halmozott frekvenciát úgy számítják ki, hogy minden frekvenciát hozzáadnak egy frekvenciaelosztási táblázatból az elődei összegéhez., Az utolsó érték mindig megegyezik az összes megfigyelés összegével, mivel az összes frekvenciát már hozzáadták az előző összeghez.

diszkrét vagy folytonos változók

változók bármely számításban a hozzájuk rendelt értékkel jellemezhetők. A diszkrét változó különálló, oszthatatlan kategóriákból áll. Egy változó és szomszédja között nem létezhet érték. Például, ha megfigyel egy óraszámot, amelyet napról napra regisztráltak, felfedezheti, hogy az osztálynak egy nap 29 hallgatója van, a másikon pedig 30 hallgató., A hallgatói részvétel azonban nem lehet 29-30 év között. (A két érték között egyszerűen nincs helye semmilyen értéknek, mivel nincs mód arra, hogy 29 és fél diák legyen.)

nem minden változót jellemeznek diszkrétnek. Egyes változók (például az idő, a magasság és a súly) nem korlátozódnak az oszthatatlan kategóriák rögzített halmazára. Ezeket a változókat folyamatos változóknak nevezzük,és végtelen számú lehetséges értékre oszthatók. Az idő például órák, percek, másodpercek és ezredmásodpercek törtrészeiben mérhető., Így ahelyett, hogy 11-12 perc alatt befejezné a versenyt, a zsoké és a lova 11 perc 43 másodperc alatt keresztezi a célvonalat.

alapvető fontosságú tudni a különbséget a két típusú változó között a halmozott gyakoriság megfelelő kiszámításához.

1. példa-diszkrét változók

A Louise-tó teljes sziklamászó száma, Alberta 30 napos időszak alatt került rögzítésre. Az eredmények a következők:

31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56, 4, 54, 39, 52, 35, 51, 63, 42.,e diszkrét változók:

• létre, szár, levél, valamint telek, (lásd a szár, levél, valamint a telkek), a további oszlopokban címkézett Frekvencia, Felső Érték Halmozott frekvencia
• kitalálni, hogy az a megfigyelések gyakorisága az egyes szár
• keresse meg a felső értéket, minden szár
• számítani a kumulatív gyakoriság hozzáadásával a számok a Frekvencia oszlop
• felvétel az eredményeket, a telek

Telken egy grafikon segítségével az y-tengely (vagy függőleges vonal) a kumulatív gyakoriság, valamint az x-tengely (vagy vízszintes vonal) az embereknek a száma, sziklamászás.,

válaszok:

1. a sziklamászók száma 4-től 65-ig terjed. Annak érdekében, hogy egy szár és levél telek, az adatok a legjobban csoportosítva osztály intervallumokban 10.

   minden intervallum a szár oszlopban található. Az oszlopon belüli számok az első számot képviselik az osztály intervallumán belül. (Például a 0 szár a 0-9 intervallumot jelenti, az 1 szár a 10-19 intervallumot, stb.)

   A levél oszlop felsorolja az egyes osztályintervallumokban található megfigyelések számát., Például a 2. szárban (20-29.intervallum) a három megfigyelést (23, 24 és 26) 3, 4 és 6-ként ábrázolják.

   A frekvencia oszlop felsorolja az osztály intervallumon belül található megfigyelések számát. Például az 5. szárban kilenc levél (vagy megfigyelés) található; az 1.szárban csak kettő van.

   a halmozott frekvencia kiszámításához használja a Frekvenciaoszlopot.

   • először adja hozzá a számot a Frekvenciaoszlopból elődjéhez. Például a Stem 0-ban csak egy megfigyelésünk van, nincsenek elődeink. A halmozott frekvencia egy.,
     1 + 0 = 1
   • az 1.szárban azonban két megfigyelés van. Adja hozzá ezt a kettőt az előző halmozott gyakorisághoz (egy), az eredmény pedig három.
     1 + 2 = 3
   • a Stem 2-ben három megfigyelés van. Ezt a hármat hozzá kell adni az előző halmozott gyakorisághoz (három), a teljes (hat) pedig a Stem 2 halmozott gyakorisága.
     3 + 3 = 6
   • folytassa ezeket a számításokat, amíg össze nem adja az összes számot a frekvencia oszlopban.
   • rögzítse az eredményeket a halmozott frekvencia oszlopban.,

   a felső Érték oszlop felsorolja azt a megfigyelést (változót), amelynek a legmagasabb értéke az egyes osztályintervallumokban van. Például az 1. szárban a két 8. és 9. megfigyelés a 18.és 19. változót jelenti. E két változó felső értéke a 19.

   1.táblázat.,>8 9

   2	19	1 + 2 = 3
   2	3 4 6	3	26	3 + 3 = 6
   3	1 5 5 7 9	5	39	6 + 5 = 11
   4	0 1 2 3 5 9	6	49	11 + 6 = 17
   5	0 1 1 2 4 4 5 6 7	9	57	17 + 9 = 26
   6	0 2 3 5	4	65	26 + 4 = 30

2. Since these variables are discrete, use the upper values in plotting the graph., Rajzolja meg a pontokat, hogy egy ogive nevű folyamatos görbét képezzen.

   mindig jelölje meg a grafikont a halmozott frekvenciával—amely megfelel a megfigyelések számának—a függőleges tengelyen.,bel a vízszintes tengely a többi változó (ebben az esetben a teljes turistára számít) az alábbiak szerint:

   

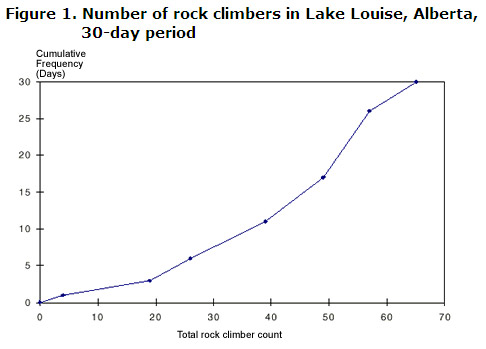
A következő információ nyerhető, akár grafikont vagy táblázatot:

• 11-től a 30 napot, 39 az emberek vagy kevesebb felmászott a szikla körül Lake Louise
• 13-án, a 30 nap, 50 vagy több ember felmászott a szikla körül Lake Louise

Ha egy folytonos változó használt, mindkét kiszámítása a kumulatív gyakoriság, ábrázolást a grafikon igényel, egy kicsit más megközelítést alkalmazott diszkrét változó.,

2. példa-folytonos változók

25 napig a Whistler-hegy hómélységét mértük (a legközelebbi centiméterre), és a következőképpen rögzítettük:

242, 228, 217, 209, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257.,

1. használja a fenti folytonos változókat:
   • állítson be egy gyakorisági eloszlási táblázatot
   • keresse meg a frekvenciát minden osztály intervallumhoz
   • keresse meg a végpontot minden osztály intervallumhoz
   • számítsa ki a halmozott frekvenciát a

gyakorisági oszlopban lévő számok hozzáadásával.

válaszok:

1. a hó mélysége 209 cm-től 266 cm-ig terjed., A frekvenciaelosztási táblázat elkészítéséhez az adatokat leginkább 10 cm-es osztályintervallumokban lehet csoportosítani.

   A hómélység oszlopban minden 10 cm-es osztály intervallum 200 cm-től 270 cm-ig szerepel.

   A frekvencia oszlop rögzíti az adott intervallumba tartozó megfigyelések számát. Ez az oszlop képviseli a megfigyelések a Tally oszlop, csak numerikus formában.,

   a végpont oszlop ugyanúgy működik, mint az 1.gyakorlat felső érték oszlopa, azzal a kivétellel, hogy a végpont az intervallum legmagasabb száma, függetlenül az egyes megfigyelések tényleges értékétől. Például a 210-220-as osztályintervallumban a két megfigyelés tényleges értéke 217 és 219. De a 219 használata helyett a 220 végpontot használják.

   a halmozott frekvencia oszlop felsorolja az elődjéhez hozzáadott összes frekvencia összegét.

   2.táblázat. Hó mélysége mért Whistler Mountain, B. C.,e2cd5a9″>

   5	240	11
   240 to < 250		7	250	18
   250 to < 260		5	260	23
   260 to < 270		2	270	25

2. Because the variable is continuous, the endpoints of each class interval are used in plotting the graph., A ábrázolt pontok össze vannak kötve, hogy ogive-t képezzenek.

   ne feledje, hogy a halmozott frekvenciát (a megfigyelések száma) a függőleges y tengelyen jelölik, és bármely más változót (hó mélysége) a vízszintes x tengelyen jelölik a 2.ábrán látható módon.,

A következő információ nyerhető, akár grafikon vagy táblázat:

• egyik a 25 nap volt a hótakaró vastagsága kevesebb, mint 200 cm
• egyik a 25 nap hó volt, mélysége kevesebb, mint 210 cm
• két hó 25 nap volt mélysége 260 cm vagy több

Egyéb kumulatív gyakoriság számítások

egy Másik számítást is kapott segítségével frekvencia engedély táblázat a relatív gyakorisági eloszlás. Ezt a módszert úgy definiáljuk, mint az egyes osztályintervallumokba tartozó megfigyelések százalékos arányát., Relatív kumulatív frekvencia megtalálható az egyes intervallumok gyakoriságának a megfigyelések teljes számával történő elosztásával. (További információkért lásd a frekvencia elosztást az adatok szervezése című fejezetben.)

a gyakorisági eloszlási táblázat is használható a kumulatív százalék kiszámításához. Ez a frekvencia-elosztási módszer megadja nekünk a kumulatív frekvencia százalékos arányát, szemben a frekvencia százalékos arányával.