hipotézisvizsgálat

A statisztikák fő célja egy hipotézis tesztelése. Például, lehet, hogy fut egy kísérletet, és úgy találja, hogy egy bizonyos gyógyszer hatásos fejfájás kezelésére. De ha nem tudja megismételni ezt a kísérletet, senki sem veszi komolyan az eredményeket. Jó példa erre a hidegfúziós felfedezés, amely homályossá vált, mert senki sem tudta megismételni az eredményeket.,

nézze meg a videót a hipotézis tesztelésének rövid áttekintéséhez, vagy olvassa el alább:

kérjük, fogadja el a statisztikákat, a marketing cookie-kat a videó megtekintéséhez.

tartalom (kattintson ide, hogy átugorja a szakaszt):

1. mi a hipotézis?
2. mi a hipotézis tesztelése?
3. Hipotézisvizsgálati példák (egy minta Z teszt).
4. hipotézis teszt átlagon (TI 83).
5. Bayesian hipotézis vizsgálat.
6. további Hipotézisvizsgálati cikkek

Lásd még:

• hipotézis tesztek egy képen
• kritikus értékek
• mi a Null hipotézis?,

segítségre van szüksége a házi feladathoz? Nézze meg a tutori oldal!

mi a hipotézis?

Andreas Cellarius hipotézis, amely a bolygó mozgását mutatja.

A hipotézis egy képzett találgatás valamiről a körülötted lévő világban. Tesztelhetőnek kell lennie, akár kísérlet, akár megfigyelés útján. Például:

• egy új gyógyszer, amelyről úgy gondolja, hogy működhet.
• egy módja a tanítás úgy gondolja, hogy jobb lehet.,
• az új fajok lehetséges helye.
• egy igazságosabb módja a szabványosított tesztek beadásának.

valójában bármi lehet, amíg tesztelheti.

mi a hipotézis állítás?

ha hipotézist javasol, szokásos nyilatkozatot írni. A kijelentése így fog kinézni:
” Ha én…(ezt egy független változóval)….ezután (ez megtörténik a függő változóval).”
például:

• Ha én (csökkentem a gyógynövényeknek adott víz mennyiségét), akkor (a gyógynövények mérete növekedni fog).,
• Ha én (a gyógyszeres kezelés mellett tanácsot adok a betegeknek), akkor (általános depressziós skálájuk csökken).
• Ha én (a vizsgákat délben 7 helyett) akkor (a hallgatói teszt pontszámai javulnak).
• Ha én (nézd meg ezt a bizonyos helyet), akkor (nagyobb valószínűséggel találok új fajokat).

egy jó hipotézis állításnak:

• tartalmaznia kell egy “HA” és “akkor” nyilatkozatot (a Kaliforniai Egyetem szerint).
• tartalmazza mind a független, mind a függő változókat.
• kísérletezéssel, felméréssel vagy más tudományosan megalapozott technikával tesztelhető.,
• a korábbi kutatásokban (akár a tiéd, akár valaki másé) szereplő információkon alapul.
• Tervezési kritériumok (mérnöki vagy programozási projektek).

mi a hipotézis tesztelése?

A hipotézis tesztelése a statisztikában egy módja annak, hogy tesztelje egy felmérés vagy kísérlet eredményeit, hogy kiderítse, van-e értelmes eredménye. Ön alapvetően teszteli, hogy az eredmények érvényesek kitalálni az esélye, hogy az eredmények véletlenül történt., Ha az eredmények véletlenül megtörténtek, a kísérlet nem lesz megismételhető, ezért kevés haszna van.

A hipotézis tesztelése a hallgatók számára az egyik leginkább zavaró szempont lehet, főleg azért, mert mielőtt még tesztet is elvégezhet, tudnia kell, mi a null hipotézis. Gyakran nehéz megfejteni azokat a trükkös szóproblémákat, amelyekkel szembesül., De könnyebb, mint gondolnád; mindössze annyit kell tennie, hogy:

1. kitalálja a null hipotézisét,
2. adja meg a null hipotézisét,
3. válassza ki, hogy milyen tesztet kell elvégeznie,
4. vagy támogassa vagy elutasítja a null hipotézist.

mi a Null hipotézis?

Ha a tudomány történetét nyomon követjük, a null hipotézis mindig az elfogadott tény. Az általánosan elfogadott null hipotézisek egyszerű példái a következők:

1. a DNS kettős spirál alakú.
2. a Naprendszerben 8 bolygó van (a Plútó kivételével).,
3. a Vioxx szedése növelheti a szívproblémák kockázatát (egy gyógyszer, amelyet most kivettek a piacról).

hogyan adhatom meg A Null hipotézist?

nem lesz szükség valódi kísérlet vagy felmérés elvégzésére az elemi statisztikákban (vagy akár megcáfolni egy olyan tényt, mint a “Plútó bolygó”!), így szóproblémákat kapnak a valós élethelyzetekből. Meg kell, hogy kitaláljuk, mi a hipotézis a probléma. Ez lehet egy kicsit trükkösebb, mint kitalálni, hogy mi az elfogadott tény. A Word problémák, keres, hogy megtalálja a tényt, hogy érvényteleníthető (azaz., valami, amit elutasíthat).

Hipotézis Tesztelése Példa #1: Alapvető Példa

A kutató úgy gondolja, hogy ha műteni beteg megy fizikai terápia hetente kétszer (ahelyett, hogy 3-szor), a felépülési idő hosszabb lesz. A térdsebészeti betegek átlagos gyógyulási ideje 8,2 hét.

a hipotézis kijelentése ebben a kérdésben az, hogy a kutató úgy véli, hogy az átlagos helyreállítási idő több mint 8, 2 hét. Matematikai értelemben írható:
H1: μ > 8.,2

ezután meg kell adnia a null hipotézist (lásd: hogyan kell megadni a null hipotézist). Ez fog történni, ha a kutató téved. A fenti példában, ha a kutató rossz, akkor a helyreállítási idő kevesebb, mint vagy egyenlő 8,2 hét. A matematikában ez:
H0 μ ≤ 8,2

A null hipotézis elutasítása

tíz évvel ezelőtt úgy gondoltuk, hogy 9 bolygó van a Naprendszerben. A Plútót 2006-ban bolygóként lefokozták. A “Plútó egy bolygó” null hipotézisét a “Plútó nem bolygó.,”Természetesen a null hipotézis elutasítása nem mindig olyan egyszerű—a kemény rész általában kitalálja, hogy mi a null hipotézis.

Hipotézisvizsgálati példák (egy minta Z teszt)

az egy minta z tesztet nem használják nagyon gyakran (mert ritkán ismerjük a tényleges populáció szórását). Jó ötlet azonban megérteni, hogyan működik, mivel ez az egyik legegyszerűbb teszt, amelyet a hipotézis tesztelésekor végezhet., Az angol osztályban meg kell tanulnod az alapokat (például a nyelvtant és a helyesírást), mielőtt megírhatnál egy történetet; gondolj egy Z minta tesztre, mint a bonyolultabb hipotézis tesztelésének megértésének alapjára. Ez az oldal két hipotézis tesztelési példát tartalmaz egy z-minta tesztelésére.

egy minta hipotézis tesztelési példák: #2

kérjük, fogadjon el statisztikákat, marketing cookie-kat a videó megtekintéséhez.

egy bizonyos iskola igazgatója azt állítja, hogy iskolájában a diákok átlag feletti intelligenciával rendelkeznek. A véletlenszerű minta harminc diák IQ pontszámok átlagos pontszám 112., Van-e elegendő bizonyíték az igazgató állításának alátámasztására? Az átlagos populáció IQ 100, szórása 15.

1. lépés: Adja meg A Null hipotézist. Az elfogadott tény az, hogy a népesség átlaga 100, tehát: H0: μ=100.

2. lépés: Adja meg az alternatív hipotézist. Az állítás az, hogy a diákok átlag feletti IQ pontszámok, így:
H1: μ > 100.
Az a tény, hogy egy bizonyos pontnál “nagyobb” pontszámokat keresünk, azt jelenti, hogy ez egy egyfarkú teszt.

3. lépés: rajzoljon egy képet a probléma megjelenítéséhez.,

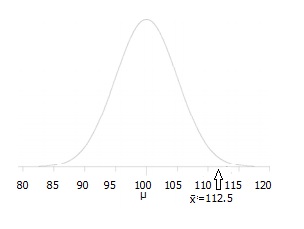
4.lépés: Adja meg az alfa szintet. Ha nem kap alfa-szintet, használjon 5% – ot (0,05).

5.lépés: Keresse meg a elutasítási régió területét (amelyet a fenti alfa szint ad meg) a z-táblázatból. Egy terület .05 egyenlő egy z-pontszám 1.645.

6. lépés: Keresse meg a tesztstatisztikát a következő képlet segítségével: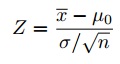
ehhez az adatkészlethez: z= (112.5 – 100) / (15/√30) = 4.56.

6. lépés: ha a 6.lépés nagyobb, mint az 5. lépés, utasítsa el a null hipotézist., Ha ez kevesebb, mint az 5. lépés, akkor nem utasíthatja el a null hipotézist. Ebben az esetben nagyobb (4, 56 > 1, 645), így elutasíthatja a null-t.

egy minta hipotézis tesztelési példák: #3

az elhízott betegek vércukorszintje átlagosan 100, standard eltérése 15. A kutató úgy gondolja, hogy a nyers kukoricakeményítőben magas étrend pozitív vagy negatív hatással lesz a vércukorszintre., A nyers kukoricakeményítő étrendet kipróbáló 30 betegből álló minta átlagos glükózszintje 140. Tesztelje azt a hipotézist, hogy a nyers kukoricakeményítő hatással volt.

* Ez a folyamat sokkal könnyebbé válik, ha TI-83 vagy Excel segítségével kiszámítja a z-pontszámot (a”kritikus érték”).,
Lásd:

• Kritikus z érték TI-83
• Z Pontszám Excel

Hipotézis Tesztelése Példák: Jelenti (A TI-83)

használhatja a TI-83 számológép hipotézis tesztelése, de a számológép nem fog rájönni, null, valamint alternatív hipotézisek; ez neked, hogy olvasd el a kérdést, a bemeneti be a számológép.

példa probléma: egy 200 fős minta átlagos életkora 21, populációs szórása (σ) 5. Tesztelje azt a hipotézist, hogy a populáció átlaga 18,9 α = 0,05.

1. lépés: Adja meg a null hipotézist., Ebben az esetben a nullhipotézis az, hogy a népesség átlaga 18,9, ezért írjuk:
H0: μ = 18,9

2.lépés: Adja meg az alternatív hipotézist. Azt akarjuk tudni, hogy a mintánk, amelynek átlaga 18,9 helyett 21, valóban különbözik-e a populációtól, ezért alternatív hipotézisünk:
H1: μ ≠ 18,9

3.lépés: Nyomja meg a Stat gombot, majd nyomja meg kétszer a jobb nyilat a tesztek kiválasztásához.

4. lépés: Nyomja meg az 1 gombot az 1:Z-Test kiválasztásához…. Nyomja meg az ENTER billentyűt.

5. lépés: a jobb nyíl segítségével válassza ki a statisztikákat.

6. lépés: Adja meg a probléma adatait:
μ0: 18.,9
σ: 5
x: 21
n: 200
μ: ≠μ0

7.lépés: lefelé mutató nyíl a számításhoz, majd nyomja meg az ENTER billentyűt. A számológép mutatja A p-érték:
p = 2,87 × 10-9

Ez kisebb, mint a mi alfa értéke .05. Ez azt jelenti, hogy el kell utasítanunk a null hipotézist.

Bayesian hipotézis tesztelése: mi ez?

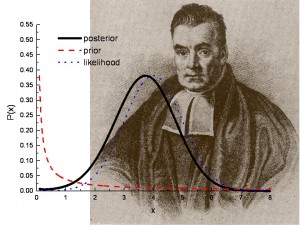
kép: Los Alamos National Lab.

Bayesian hipotézis vizsgálat segít megválaszolni a kérdést: Meg lehet-e ismételni egy teszt vagy felmérés eredményeit?
Miért érdekel, ha egy tesztet meg lehet ismételni?, Tegyük fel, hogy húsz ember ugyanabban a faluban leukémiával jött le. A kutatók egy csoportja szerint a mobiltelefon-tornyok hibásak. Egy másik tanulmány azonban megállapította, hogy a mobiltelefon-tornyoknak semmi köze sincs a falu rákos klaszteréhez. Valójában azt találták, hogy a rákok teljesen véletlenszerűek. Ha ez lehetetlennek hangzik, akkor valójában megtörténhet! A rák klaszterei egyszerűen véletlenül történhetnek. Számos oka lehet annak, hogy az első vizsgálat hibás volt., Az egyik fő ok az lehet, hogy csak nem vették figyelembe, hogy néha a dolgok véletlenszerűen történnek, csak nem tudjuk, miért.

p értékek.

jó tudomány, ha tudatja az emberekkel, hogy a tanulmányi eredményei szilárdak-e, vagy véletlenül megtörténhettek-e. Ennek szokásos módja az eredmények p-értékkel történő tesztelése. A p érték olyan szám, amelyet egy hipotézis teszt futtatásával kap az adatain. A p értéke 0,05 (5%) vagy annál kevesebb általában elég ahhoz, hogy azt állítják, hogy az eredmények megismételhetők., Van azonban egy másik módja annak, hogy tesztelje az eredmények érvényességét: Bayesian hipotézis tesztelés. Ez a fajta tesztelés ad egy másik módja annak, hogy teszteljék az erejét az eredményeket.

Bayesian hipotézis vizsgálat.

a hagyományos tesztelés (az a típus, amellyel valószínűleg az elemi statisztikákban vagy az AP statisztikákban találkozott)nem Bayesian. Ez az, hogy milyen gyakran történik az eredmény a kísérlet ismételt futtatása során. Ez egy objektív nézet arról, hogy egy kísérlet megismételhető-e.
Bayesian hypothesist testing is a subjective view of the same thing., Figyelembe veszi, hogy mennyi hit van az eredményekben. Más szóval, fogadna pénzt a kísérlet eredményére?

különbségek a hagyományos és a bayesi hipotézisek vizsgálata között.

hagyományos tesztelés (nem Bayesian) megköveteli, hogy ismételje meg a mintavételt újra és újra, míg Bayesian tesztelés nem. A kettő közötti fő különbség a tesztelés első lépése: valószínűségi modell megadása. A Bayesian tesztelés során ehhez a lépéshez előzetes ismereteket ad hozzá., Szükség van egy hátsó valószínűség használatára is, amely a véletlenszerű eseményhez adott feltételes valószínűség, miután az összes bizonyítékot figyelembe vették.

érvek Bayesian vizsgálat.

sok kutató úgy gondolja, hogy ez jobb alternatíva a hagyományos teszteléshez, mert:

1. tartalmazza az adatokkal kapcsolatos előzetes ismereteket.
2. figyelembe veszi az eredményekkel kapcsolatos személyes hiedelmeket.

ellenérvek.

1. előzetes adatok vagy ismeretek feltüntetése nem indokolt.
2. nehéz kiszámítani, mint a nem Bayes-vizsgálat.,

vissza a tetejére

Hipotézisvizsgálati cikkek

alapjai:

1. mi az Ad Hoc tesztelés?
2. kompozit hipotézis teszt
3. mi az elutasítási Régió?
4. mi a Kétfarkú teszt?
5. hogyan lehet eldönteni, hogy egy hipotézis teszt egy farkú teszt vagy Kétfarkú teszt.
6. hogyan lehet eldönteni, hogy egy hipotézis bal farkú teszt vagy jobb farkú teszt.
7. Hogyan állapítható meg A Null hipotézis statisztikában.
8. hogyan lehet megtalálni a kritikus értéket.
9. hogyan lehet támogatni vagy elutasítani a Null hipotézist.,

specifikus tesztek:

1. ANOVA.
2. Brunner Munzel Test (Generalized Wilcoxon Test)
3. Chi Square Test for Normality
4. Cochran-Mantel-Haenszel Test

F Test

5. Granger Causality Test.
6. Hotelling ‘ s t-Squared
7. KPSS Test.
8. mi a valószínűségi Arány teszt?
9. Log rank teszt.
10. MANCOVA
11. szekvenciális valószínűségi Arány teszt
12. Jelteszt futtatása.
13. T teszt: egy minta.
14. T-teszt: két minta.
15. Welch ‘ s ANOVA.
16. Welch ‘ s Test for Unquest Variancis.,
17. Z-teszt: egy minta.
18. Z teszt: két Arány
19. Wald teszt.

1. mi az Elfogadó Régió?
2. hogyan kell kiszámítani Chebyshev tételét.
3. döntési szabály.
4. szabadságfok.
5. irányított teszt
6. hamis felfedezési Arány
7. a legkevésbé jelentős különbség kiszámítása.
8. szintek a statisztikákban.
9. a hibahatár kiszámítása.
10. átlagos különbség (különbség az eszközökben)
11. a többszörös tesztelési probléma.
12. mi a Neyman-Pearson Lemma?
13. egy minta medián teszt.,
14. REGWF
15. hogyan lehet megtalálni a minta méretét (Általános utasítások).
16. Sig 2 (farkú) jelentése eredmények
17. mi a szabványosított vizsgálati statisztika?
18. Standard Error
19. standardizált értékek: példa.
20. hogyan kell kiszámítani a T-pontszámot.
21. T-Score Vs. A Z. Score.
22. egyetlen átlag tesztelése.
23. egyenlőtlen mintaméretek.
24. egységesen legerősebb tesztek.
25. hogyan kell kiszámítani a Z-pontszámot.

——————————————————————————

segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez?, A Chegg tanulmány segítségével lépésről-lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!