- történelmi háttér
- látszólagos magnitúdó, m
- a csillagok távolságának meghatározása – távolság Modulus
- név & Csillagok azonosítása
abszolút magnitúdó, M
Magnitude / távolság számítások
tanulmányozza az alább látható csillagtérképeket. Megmutatja az égbolt egy részét a Crux csillagkép körül, amelyet általában déli keresztnek neveznek. Mozgassa a kurzort a fényképen, hogy azonosítsa néhány csillagot.
melyik csillag a legfényesebb?,

ha válaszol Alpha (α)Centauri, a csillag a bal alsó sarokban a fénykép jobb. Mint látható, egy ilyen fényképészeti kép sokkal több csillagot mutat, mint amennyit szabad szemmel láthat. Ennek ellenére egyes csillagok kiemelkedőbbek, mint mások. Az α Centauri kiválasztásakor néhány feltételezést tett. Mik voltak?
egy ilyen fénykép fényes csillagokat mutat nagyobb lemezekként, mint a halványabb csillagok., Ez azt jelenti, hogy ezek a csillagok fizikailag nagyobbak, mint a fénykép halványabb csillagai? Ne feledje, hogy az asztrometriai szakaszban megtudtuk, hogy a Napunkon kívüli összes csillag olyan távoli, hogy hatékonyan pontforrások. Miért jelennek meg néhányan fényesebbek (a szemünknek) vagy nagyobbak (fényképeken), mint mások? Valójában mi a fényerő, és hogyan mérhetjük meg? Ezekre a kérdésekre adott válaszok képezik e szakasz középpontjában.,
történelmi háttér

a csillagok fényességének mérése és összehasonlítása a görög csillagászra és matematikusra vezethető vissza (IE 190-120). Az ókor egyik legnagyobb csillagásza, 850 csillagból álló katalógust készít, pozíciókkal és összehasonlító fényességekkel., Rendszerében a legfényesebb csillagokat 1-es nagyságrend, a következő legfényesebb 2-es magnitúdó stb.rendelték a leggyengébb csillagokhoz, amelyek csak a szabad szemmel láthatók, amelyek 6-os nagyságúak voltak. Ez a hatpontos skála Rangsor, az első osztályú csillagok, a legfényesebbek, az első magnitúdók, a halvány alacsony sebességű csillagok pedig a hatodik magnitúdók voltak.
az 1600-as évek elején távcsövekkel rendelkező halványabb csillagok felfedezése szükségessé tette a skála kiterjesztését a 6.magnitúdón túl., A vizuális fotométerek, a csillagok intenzitásának mérésére szolgáló eszközök fejlesztése, a tizenkilencedik században John Herschel és mások arra késztették a csillagászokat, hogy nemzetközi szabványt fogadjanak el. Az a tény, hogy a szem érzékeli különbségek intenzitás logaritmikusan pedig lineárisan találtak az 1830-as években. 1856-ban Norman Pogson javasolt, hogy egy csillag nagyságrendű 1 100 × fényesebb, mint egy csillag nagyságrendű 6. Az egy nagyságú különbség tehát 5√100 = 2, 512-szeres fényerővel egyenlő.,
látszólagos magnitúdó, m
a csillag látszólagos nagysága, m, az a nagyság, amelyet egy megfigyelő látott a Földön.
egy nagyon fényes tárgy, például a nap vagy a Hold negatív látszólagos nagyságrendű lehet. Bár Hipparkhosz eredetileg rendelt a legfényesebb csillagok, hogy egy nagysága 1 óvatosabb összehasonlítás azt mutatja, hogy a legfényesebb csillag az éjszakai égbolton, Sirius vagy α Canis Majoris (CMa) valójában egy látszólagos nagysága, m = -1.44. A Hipparchus eredeti értékeinek újrakalibrálásával a Vega fényes csillag most úgy van meghatározva, hogy látszólagos nagysága 0, 0.,
a halvány csillagok teleszkópos felfedezése után az 1600-as évek elején a magnitúdó skálát a 6-os magnitúdónál kisebb objektumokra is ki kellett terjeszteni. Az alábbi táblázat az égi objektumok látszólagos nagyságának tartományát mutatja.
| Objektum | Látszólagos Nagysága |
|---|---|
| Napot |
-26.5
|
| Telihold |
-12.5
|
| a Vénusz |
-4.,3
|
| Mars or Jupiter |
-2
|
| Sirius (α CMa) |
-1.44
|
| Vega (α Lyr) |
0.0
|
| Alnair (α Gru) |
1.73
|
| Naked-eye limit |
6.5
|
| Binocular limit |
10
|
| Proxima Cen |
11.,09
|
| Visual limit through 20 cm telescope |
14
|
| QSO at redshift z = 2 |
≈ 20
|
| Cepheid in galaxy M100 observed with HST |
26
|
| Galaxy at z = 6 observed with Gemini 8.1 m telescope |
28
|
| Limit for James Webb Space Telescope |
≥ 30
|
If a star of magnitude 1 is 2.,512 × fényesebb, mint egy 2-es és 100-as magnitúdójú csillag, &szer fényesebb, mint egy hatodik magnitúdójú csillag mennyivel világosabb, mint egy 3-as magnitúdójú csillag? Itt óvatosnak kell lenned. Ez nem egyszerűen 2 × 2,512 különböző. Ne feledje, hogy egy nagyságú különbség 5√100 = 2, 512. Ezért 2 nagyságú különbség = 2,5122 = 6,31 × fényerő különbség.
két objektum különböző nagyságú ezért változik a fényerő 2.512 emelt a hatalom te nagysága különbség., Ha ezt egyenletként írjuk, akkor a fényerő vagy intenzitás arányát, az IA / IB-t két objektum, az A és B között, a ma és mB nagyságokkal a következő egyenlet adja meg:
vessünk egy pillantást egy példára.
1. példa: két csillag összehasonlítása.
mennyivel világosabb az Alnair, látszólagos nagysága +1, 73, mint a Proxima Cen, 11, 09 magnitúdóval?
a 4.1 egyenlet segítségével:
so, helyettesítve:
2. példa: mennyivel világosabb a nap, mint a telihold?
erre emlékeztetünk a fenti táblázatból, hogy a Nap látszólagos nagysága -26,5, a telihold pedig – 12,5.
tehát a 4.1-es egyenlet használatával kapjuk:
a helyettesítés megadja nekünk:
fontos megjegyezni, hogy a magnitúdó egyszerűen egy szám, nincs egysége. A látszólagos nagyságrendű szimbólum egy kisebb eset m; ezt minden probléma esetén egyértelművé kell tennie.
abszolút magnitúdó, M
mit mond nekünk az a tény, hogy a Sirius látszólagos nagysága -1,44, a Betelgeuse pedig 0,45 látszólagos magnitúdója? Egy másik gondolkodásmód az, hogy megkérdezzük, miért Sirius A legfényesebb csillag az éjszakai égbolton?, A csillag két fő okból is fényesnek tűnhet:
- lehet, hogy belső fényű, vagyis az elektromágneses sugárzás erős kibocsátója, vagy
- nagyon közel lehet hozzánk, vagy mindkettőhöz.
a csillag látszólagos nagysága tehát részben attól függ, hogy milyen távolságra van tőlünk. Valójában Sirius fényesebbnek tűnik, mint a Betelgeuse, pontosan azért, mert Sirius nagyon közel van hozzánk, csak 2.6 pc-re, míg a Betelgeuse körülbelül 160 pc-re van., Az a felismerés, hogy a csillagok nem mindegyike azonos fényerővel rendelkezik, azt jelentette, hogy a látszólagos magnitúdó önmagában nem elegendő a csillagok összehasonlításához. Kifejlesztettek egy új rendszert, amely lehetővé tenné a csillagászok számára, hogy közvetlenül összehasonlítsák a csillagokat. Ezt a rendszert abszolút nagyságnak nevezik, M.
egy csillag abszolút nagysága, m, az a nagyság, amely a csillagnak akkor lenne, ha 10 parszek távolságra lenne tőlünk. A távolság 10 pc tisztán önkényes, de most nemzetközileg elfogadott csillagászok., Az abszolút magnitúdó skálája megegyezik a látszólagos magnitúdóval, azaz az 1 magnitúdó különbsége = 2, 512-szeres fényerő-különbség. Ez a logaritmikus skála is nyílt végű és unitless. Ismét minél alacsonyabb vagy negatívabb az M értéke, annál világosabb a csillag. Az abszolút nagyság kényelmes módja a csillag fényességének kifejezésére. Miután egy csillag abszolút nagysága ismert, összehasonlíthatja azt más csillagokkal is. A Betelgeuse, M = -5,6 lényegében fényesebb, mint a Sirius, m = 1,41-gyel.
napunk abszolút vizuális nagysága 4, 8.,
A csillagoktól való távolság meghatározása-távolság Modulus
amint az asztrometria szakaszából emlékeztethet, a legtöbb csillag túl távoli ahhoz, hogy parallaxisát közvetlenül mérjék. Mindazonáltal, ha ismeri mind a csillag látszólagos, mind abszolút nagyságát, meghatározhatja annak távolságát. Nézzük meg újra Sirius és Betelgeuse plusz egy másik csillag nevű GJ 75.
milyen messze van a GJ 75? Ez egy szokatlan csillag, mivel látszólagos és abszolút nagyságai azonosak. Miért? Ennek oka az, hogy valójában 10 parszek távol van tőlünk, tehát definíció szerint két nagyságának azonosnak kell lennie.,
mi a helyzet Siriusszal? Látszólagos nagysága alacsonyabb (ezért világosabb), mint abszolút nagysága. Ez azt jelenti, hogy közelebb van hozzánk, mint 10 Parsec. A Betelgeuse látszólagos nagysága magasabb (tehát halványabb), mint abszolút nagysága, így még fényesebbnek tűnik az éjszakai égbolton, ha csak 10 parszek távolságra lenne.
A csillagászok a látszólagos és az abszolút magnitúdó, a távolság modulus közötti különbséget használják a csillagtól való távolság meghatározásának módjaként.
- távolság Modulus = M – M.
- távolság modulus negatív csillagok közelebb 10 parszecs.,
- távolság modulus pozitív csillagok távolabb, mint 10 parszek.
- a távolságmodulus mérete határozza meg a távolság tényleges értékét, így az 1.5 távolságmodulus csillag közelebb van, mint egy, 8.7 távolságmodulával.
magnitúdó/távolság számítások
a távolság modulus lehet használni, hogy meghatározzák a távolság a csillag az egyenlet segítségével:
ahol d a parsecs. Vegye figyelembe, hogy ha d = 10 pc, akkor m és M ugyanaz. (Ennek az egyenletnek a formális levezetése a fényesség következő oldalán található)., Az NSW HSC Syllabus Képletlap a következő egyenletet tartalmazza:
de ez egyszerűen a 4.2 egyenlet átdolgozása. Kényelmesnek kell lennie ennek az egyenletnek a megoldásában, tekintettel a három változó bármelyikére. Tudassa velünk, nézd meg, hogyan lehet megoldani néhány példát.
3. példa: adott m és d, meg kell találni M.
β Crucis (vagy mimóza) látszólagos nagysága 1,25 és 108 parszecs távoli. Mi az abszolút nagysága?
a 4.3 egyenlet segítségével:
tehát a β Crucis abszolút nagysága -3.92
Megjegyzés Ez a számítás teljes munkát mutatott, hogy minden lépés explicit legyen. (Ne feledje, hogy a magnitúdóegyenletek megoldása során a log a logaritmusokat a 10-es alapra, nem pedig a természetes logaritmusokat vagy az ln-t jelenti.)
4. példa: adott m és M, keresse meg d.
a Betelgeuse látszólagos nagysága 0,45 és abszolút nagysága -5,14. Milyen messze van?
Ez a probléma megköveteli, hogy átírjuk a 4.2 egyenletet, hogy D-t ismeretlenként adjuk meg., Ezt mutatja az alábbi:
ami lehet írni, mint:
most helyettesítik a:
tehát Betelgeuse körülbelül 130 pc távoli.
ismét ez a példa teljes munkát mutat, míg a valóságban előfordulhat, hogy nem mutat minden lépést., Fontos azonban, hogy a munka, hogy az ilyen problémák egyértelműen, így ellenőrizni tudja az algebrai manipuláció és a helyettesítések. Munka naplók, indexek lehet trükkös, így biztosítani tudja, hogyan kell csinálni ezeket a számológép.
5. példa: adott M és d, keresse m.
a gyakorlatban ez a fajta probléma kevésbé reális a tényleges tárgyak, mint mi általában mérni a látszólagos nagyságok közvetlenül azonban lehet, hogy szeretnénk kiszámítani, hogy milyen látszólagos nagysága egy osztály vagy típusú objektum adott a többi paramétert. Ismét, kezdve egyenlet 4.,3 határozzuk meg, hogy egy olyan szuperóriás, mint a Deneb, abszolút nagyságú -8.73, milyen fényes lenne, ha 230 parszek távolságra lenne.
szóval helyettesítik a:
tehát Deneb volna egy látszólagos nagysága -1.89. Ez fényesebbé tenné az éjszakai égbolton, mint Sirius (m = -1.44)., A valóságban Deneb körülbelül 990 pc távoli, bár ez az érték nagy bizonytalansággal rendelkezik.
6. példa: mi van, ha D-t nem adják meg, hanem parallax,p-t adnak?
ez valójában nagyon egyenesen előre. Emlékezzünk vissza az asztrometriai szakaszból, hogy közvetlen kapcsolat van a távolság és a parallaxis között.
így egyszerűen be kell illesztenie ezt a 4.2 vagy 4.3 egyenletbe.
névadó & Csillagok azonosítása
tudassa velünk, hogy a Crux fotója és az oldal tetején található mutatók., Az alábbi fotó ugyanazt a régiót mutatja a kiemelkedő csillagokkal. Látható a látszólagos nagyságuk is. A Crux egy csillagkép, amely egyike annak a 88 régiónak, amelybe az égi szférát a csillagászok nemzetközi szinten felosztották és megállapodtak. A Crux valójában a legkisebb csillagkép, amely könnyen azonosítható a déli égbolton. A kiemelkedő közeli csillagok gyakran nevezik a Mutatók valójában része egy nagy constellation nevű Kentaur.

most már észreveheti, hogy a csillagokat a görög ábécé betűivel nevezték el; α, β, γ δ És ε (alfa, béta, gamma, delta, epszilon az első öt), majd az egyes konstellációk standard hárombetűs rövidítése (Cru a Crucis vagy a Crux és Cen a Centaurus esetében). Ha alaposan megnézzük a Crux öt megnevezett csillagának látszólagos nagyságát, látni fogjuk, hogy a legfényesebb csillag α, a következő β stb., Ezt a rendszert Bayer rendszernek hívják, Johann Bayer után, aki 1603-ban mutatta be. A csillagkép legfényesebb csillaga az α betű, a következő β stb. E szabály alóli kivétel a &alpha Orionis vagy Betelgeuse. Valójában halványabb, mint a β Ori, a Rigel kis mennyiségben. Ez egy érdekes történelmi eset, amelyet az a felismerés old meg, hogy a Betelgeuse fényereje kissé elhalványult, mivel a Bayer rendszer alatt nevezték el.,
a csillagképekről való emlékezés egyik pontja az, hogy a csillagképen belüli csillagok általában nem fizikailag kapcsolódnak egymáshoz, ellentétben a klaszterek csillagaival. Az a tény, hogy úgy tűnik, közel egymáshoz tisztán igazítás hatása mentén túra látómező. Valójában a fenti régió csillagai széles körben el vannak választva tőlünk, amint az a következő képen látható.
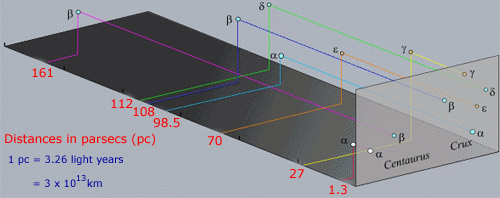
néhány fényes csillagnak, például az α Cen-nek is van saját neve. A Sirius (α Sco) egy ilyen példa, míg az α Cen-t Rigel Kentaurusnak is nevezik. Számos csillagnév arab eredetű abból a korból, amikor a görög feljegyzések megmaradtak és az Iszlám csillagászok fejlesztették ki őket. A csillagok elnevezésének Bayer-rendszerével az a probléma, hogy a görög ábécében csak 24 betű van, de sokkal több csillag van, mint az egyes csillagképekben.
a legtöbb csillagnak valójában nincs konkrét neve vagy Bayer besorolása., Manapság a csillagászok hatalmas csillagkatalógusokat állítottak össze, néhányuk több mint 10 millió objektummal rendelkezik, így a legtöbb csillagnak csak katalógusszáma van. A csillagoknak egynél több azonosító neve vagy katalógusszáma lehet, attól függően, hogy hány katalógusban vannak. A változó csillag, δ Cep például HIP 110991, SAO 34508 vagy bármely több mint 30 más azonosítók néven is ismert! Sok katalógus égi koordinátákat használ, mint például a helyes felemelkedés és a deklináció az objektumok azonosításához. Így δ cep ismert IRAS 22273+5809, CCDM J22292 + 5825A és AAVSO 2225+57., A katalógusok RA és dec változásainak enyhe eltérése a csillagok megfelelő mozgásának és a referenciakeret precessziójának köszönhető.