Hypoteesin Testaus
 päätarkoitus tilastot on testata hypoteesi. Saatat esimerkiksi tehdä kokeen ja huomata, että tietty lääke on tehokas päänsärkyjen hoidossa. Mutta jos et voi toistaa tuota kokeilua, kukaan ei ota tuloksiasi vakavasti. Hyvä esimerkki tästä oli kylmä fuusio löytö, joka raukesi unohduksiin, koska kukaan ei voi kopioida tulokset.,
päätarkoitus tilastot on testata hypoteesi. Saatat esimerkiksi tehdä kokeen ja huomata, että tietty lääke on tehokas päänsärkyjen hoidossa. Mutta jos et voi toistaa tuota kokeilua, kukaan ei ota tuloksiasi vakavasti. Hyvä esimerkki tästä oli kylmä fuusio löytö, joka raukesi unohduksiin, koska kukaan ei voi kopioida tulokset.,
Katso video lyhyt katsaus hypoteesin testaus, tai lukea alla:
sisältö (klikkaa hypätäksesi osioon):
- mikä on hypoteesi?
- mikä on Hypoteesitestaus?
- Hypoteesitestausesimerkkejä (yksi näyte Z-testi).
- Hypoteesitesti keskiarvolla (TI 83).
- Bayesilainen Hypoteesitestaus.
- Enemmän Hypoteesin Testaus Artikkeleita
Katso myös:
- Hypoteesi Testit Yksi Kuva
- Kriittiset Arvot
- Mikä on nollahypoteesi?,
Tarvitsetko apua läksyongelmaan? Tsekkaa tutorointisivumme!
Mikä on Hypoteesi?

Andreas Cellarius hypoteesi, osoittaa planeettojen liikkeet.
hypoteesi on valistunut arvaus siitä jotain maailmassa ympärilläsi. Sen pitäisi olla testattavissa joko kokeilemalla tai havainnoimalla. Esimerkiksi:
- uusi lääke luulet saattaisi toimia.
- tapa opettaa luulet voisi olla parempi.,
- uusien lajien mahdollinen sijainti.
- oikeudenmukaisempi tapa antaa standardoituja testejä.
se voi olla oikeastaan mitä tahansa, kunhan sen voi laittaa testiin.
mikä on hypoteesi lausuma?
Jos aiot ehdottaa hypoteesia, on tapana kirjoittaa lausunto. Lausuntosi näyttää tältä:
” If I…(do this to an independent variable)….sitten (tämä tapahtuu riippuvainen muuttuja).”
esimerkiksi:
- Jos minä (vähentää määrä vettä annetaan yrttejä) sitten (yrtit kasvaa kokoa).,
- Jos I (anna potilaille neuvontaa lääkityksen lisäksi) silloin (heidän masennusasteikkonsa laskee).
- Jos I (anna tentit keskipäivällä 7: n sijaan) niin (ylioppilaskokeiden pisteet paranevat).
- Jos minä (katso tätä tiettyä paikkaa) sitten (löydän todennäköisemmin uusia lajeja).
hyvä hypoteesi lausunto olisi:
- Sisältää ”jos” ja ”sitten” – käskyn (mukaan University of California).
- sisältää sekä riippumattomat että riippuvaiset muuttujat.
- on testattavissa kokeilun, tutkimuksen tai muun tieteellisesti äänitekniikan avulla.,
- perustuu aikaisemman tutkimuksen tietoihin (joko sinun tai jonkun muun tietoihin).
- on suunnittelukriteerit (suunnittelu-tai ohjelmointihankkeille).
mikä on Hypoteesitestaus?

Hypoteesin testaus tilastoissa on tapa, jolla voit testata tulokset tutkimuksen tai kokeilun nähdä, jos sinulla on mielekkäitä tuloksia. Testaat, ovatko tuloksesi kelvollisia-selvittämällä todennäköisyydet, että tuloksesi ovat sattuneet sattumalta., Jos tulokset ovat voineet tapahtua sattumalta, kokeilu ei ole toistettavissa ja niin on vähän käyttöä.
Hypoteesin testaus voi olla yksi kaikkein sekava näkökohtia opiskelijoille, lähinnä koska ennen kuin voit jopa suorittaa testin, sinun täytyy tietää, mitä teidän nollahypoteesi on. Usein niitä hankalia sanaongelmia, joita joudut kohtaamaan, voi olla vaikea tulkita., Mutta se on helpompaa kuin luulet; kaikki sinun tarvitsee tehdä, on:
- Selvittää nollahypoteesi,
- Valtion nollahypoteesi,
- Valitse, millainen testi sinun täytyy tehdä,
- Joko tukea tai hylätä nollahypoteesi.
Mikä on nollahypoteesi?
Jos seuraa tieteen historiaa, nollahypoteesi on aina hyväksytty tosiasia. Yksinkertaisia esimerkkejä nollahypoteeseista, jotka yleisesti hyväksytään todeksi, ovat:
- DNA on kaksoiskierteen muotoinen.
- aurinkokunnassa on 8 planeettaa (Plutoa lukuun ottamatta).,
- Vioxxin ottaminen voi lisätä sydänvaivojen riskiä (lääke, joka otetaan nyt pois markkinoilta).
miten lausun nollahypoteesin?
Sinun ei tarvitse oikeastaan tehdä todellinen koe tai tutkimus peruskoulun tilastot (tai jopa kumota se, kuin ”Pluto on planeetta”!), joten saat sanaongelmia tosielämän tilanteista. Sinun täytyy selvittää, mikä hypoteesi on ongelma. Tämä voi olla hieman hankalampaa kuin vain selvittää, mikä hyväksytty tosiasia on. Sanaongelmien kanssa etsit tosiasiaa, joka on mitätön (ts., jotain voit hylätä).
Hypoteesin Testaus Esimerkkejä #1: yksinkertainen Esimerkki
tutkija uskoo, että jos polvi leikkausta potilaat mennä fysioterapiaa kaksi kertaa viikossa (sen sijaan 3 kertaa), niiden toipumisaika on pidempi. Polvileikkauspotilaiden toipumisajat ovat keskimäärin 8,2 viikkoa.
hypoteesi lausunnon tähän kysymykseen on, että tutkija uskoo, keskimääräinen toipumisaika on yli 8.2 viikkoa. Se voidaan kirjoittaa matemaattisesti seuraavasti:
H1: μ > 8.,2
seuraavaksi on ilmoitettava null-hypoteesi (Katso: miten null-hypoteesi esitetään). Niin käy, jos tutkija on väärässä. Yllä olevassa esimerkissä, jos tutkija on väärässä, palautumisaika on alle tai yhtä suuri kuin 8,2 viikkoa. Matematiikka, joka on:
H0 μ ≤ 8.2
Hylkää nollahypoteesi
Kymmenen vuotta sitten, uskoimme, että siellä oli 9 planeettojen aurinkokunnan. Pluto alennettiin planeetaksi vuonna 2006. Nollahypoteesin ” Pluto on planeetta ”korvasi” Pluto ei ole planeetta.,”Nollahypoteesin hylkääminen ei tietenkään ole aina niin helppoa—vaikeinta on yleensä selvittää, mikä nollahypoteesi ylipäätään on.
Hypoteesin Testaus Esimerkkejä (Yhden Otoksen Z-Testi)
yhden otoksen z-testi ei käytetä kovin usein (koska me harvoin tiedämme, todellinen perusjoukon keskihajonta). On kuitenkin hyvä ymmärtää, miten se toimii, koska se on yksi yksinkertaisimmista testeistä, joita voit tehdä hypoteesitestauksessa., Englannin tunnilla sai opetella perusasiat (kuten kielioppi ja oikeinkirjoitus) ennen kuin pystyi kirjoittamaan tarinan; ajattele yhtä näytettä z-testit perustaksi monimutkaisemman hypoteesitestauksen ymmärtämiselle. Tällä sivulla on kaksi hypoteesitestausesimerkkiä yhdelle näytteelle z-testit.
Yksi Näyte Hypoteesin Testaus Esimerkkejä: #2
erään koulun rehtori väittää, että hänen koulunsa oppilaat ovat keskimääräistä älykkäämpiä. Kolmisenkymmentä opiskelijaa käsittävän satunnaisotoksen ÄLYKKYYSOSAMÄÄRIEN keskiarvo on 112., Onko rehtorin väitteen tueksi riittävästi todisteita? Keskimääräinen väestön ÄLYKKYYSOSAMÄÄRÄ on 100 ja keskihajonta 15.
Vaihe 1: ilmoitetaan nollahypoteesi. Hyväksytty tosiasia on, että populaation keskiarvo on 100, joten: H0: μ=100.
Vaihe 2: ilmoitetaan vaihtoehtoinen hypoteesi. Väite on, että opiskelijoilla on keskimääräistä enemmän ÄLYKKYYSOSAMÄÄRIÄ, joten:
H1: μ > 100.
se, että etsimme pistemääriä” suurempi kuin ” tietty piste tarkoittaa, että kyseessä on yksipyrstöinen testi.
Vaihe 3: Piirrä kuva, jonka avulla voit visualisoida ongelman.,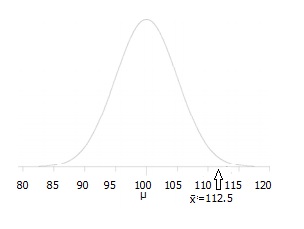
Vaihe 4: ilmoitetaan alfataso. Jos sinulle ei anneta alfatasoa, Käytä 5% (0,05).
Vaihe 5: Etsi hylkääminen alueen (antama alfa-tason yläpuolella) z-taulukko. Alue .05 vastaa z-lukemaa 1,645.
Vaihe 6: Löytää testimuuttuja käyttämällä tätä kaavaa: 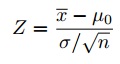
tästä joukko tietoja: z= (112.5 – 100) / (15/√30) = 4.56.
Vaihe 6: jos Vaihe 6 on suurempi kuin Vaihe 5, hylkää nollahypoteesi., Jos se on alle vaihe 5, et voi hylätä nollahypoteesi. Tässä tapauksessa, se on suurempi (4.56 > 1.645), joten voit hylätä null.
Yksi Näyte Hypoteesin Testaus Esimerkkejä: #3
lihavien potilaiden veren glukoosipitoisuuksien keskiarvo on 100 ja keskihajonta 15. Tutkija arvelee, että runsaasti raakaa maissitärkkelystä sisältävällä ruokavaliolla on positiivinen tai negatiivinen vaikutus veren glukoosipitoisuuksiin., 30 raakaa maissitärkkelysruokavaliota kokeilleesta potilaasta otetun näytteen glukoosipitoisuus on keskimäärin 140. Testaa hypoteesi, että raaka maissitärkkelyksellä oli vaikutusta.
*Tämä prosessi on paljon helpompaa, jos käytät TI-83 tai Excel laskea z-score (”kriittinen arvo”).,
Katso:
- Kriittinen z-arvo TI-83
- Z Pisteet Excel
Hypoteesin Testaus Esimerkkejä: Keskiarvo (Käyttäen TI-83)
Voit käyttää TI-83 laskin hypoteesin testaus, mutta laskin ei selvittää, null ja vaihtoehtoisia hypoteeseja; se on jopa voit lukea kysymys ja syöttää sen laskin.
Esimerkkiongelma: 200 ihmisen otoksen keski-ikä on 21 ja populaation keskihajonta (σ) 5. Testaa hypoteesi, jonka mukaan populaation keskiarvo on 18,9 α = 0,05.
Vaihe 1: ilmoitetaan nollahypoteesi., Tässä tapauksessa nollahypoteesi on, että populaation keskiarvo on 18,9, niin kirjoitetaan:
H0: μ = 18.9
Vaihe 2: Valtion vaihtoehtoinen hypoteesi. Haluamme tietää, jos meidän näyte, joka on siis 21 sen sijaan, 18.9, todella on erilainen väestö, siksi meidän vaihtoehtoinen hypoteesi:
H1: μ ≠ 18.9
Vaihe 3: Paina Stat sitten paina oikeaa nuolta kaksi kertaa valitse TESTIT.
Vaihe 4: Paina 1 valitaksesi 1: Z-testin…. Paina ENTER.
Vaihe 5: Valitse tilastot oikealla nuolella.
Vaihe 6: Anna tiedot ongelmasta:
μ0: 18.,9
σ: 5
x: 21
n: 200
μ: ≠μ0
Vaihe 7: Nuoli alas, jos haluat Laskea ja paina ENTER-näppäintä. Laskin osoittaa, p-arvo:
p = 2.87 × 10-9
Tämä on pienempi kuin alfa-arvo .05. Se tarkoittaa, että meidän pitäisi hylätä nollahypoteesi.
Bayesilainen Hypoteesikoe: mikä se on?
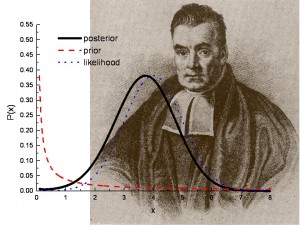
Kuva: Los Alamosin Kansallisessa Laboratoriossa.
Bayesilainen hypoteesitestaus auttaa vastaamaan kysymykseen: Voidaanko testin tai tutkimuksen tulokset toistaa?
miksi välitämme, jos testi voidaan toistaa?, Sanotaan, että kaksikymmentä ihmistä samassa kylässä sairastui leukemiaan. Tutkijaryhmä toteaa, että syynä ovat kännykkätornit. Toisessa tutkimuksessa kävi kuitenkin ilmi, että kännykkätorneilla ei ollut mitään tekemistä kylän syöpäklusterin kanssa. Syöpien todettiin olevan täysin sattumanvaraisia. Jos se kuulostaa mahdottomalta, se voi todella tapahtua! Syöpäklusterit voivat tapahtua yksinkertaisesti sattumalta. Ensimmäiseen tutkimukseen saattoi olla monia syitä., Yksi tärkeimmistä syistä, voi olla, että he eivät ota huomioon, että joskus asioita tapahtuu satunnaisesti ja me vain tiedä, miksi.
p-arvot.
on hyvä tiedettä kertoa ihmisille, ovatko tutkimustuloksesi vankkoja vai olisiko ne voineet tapahtua sattumalta. Tavallinen tapa on testata tuloksesi p-arvolla. P-arvo on luku, jonka saat tekemällä hypoteesitestin tiedoistasi. P-arvo 0,05 (5%) tai vähemmän riittää yleensä väittämään, että tulokset ovat toistettavissa., On kuitenkin toinenkin tapa testata tulosten oikeellisuutta: Bayesilainen Hypoteesitestaus. Tällainen testaus antaa sinulle toisen tavan testata tulosten voimaa.
Bayesilainen Hypoteesitestaus.
Perinteinen testaus (tyyppi olet luultavasti tuli koko peruskoulun tilastot tai AP tilastot) kutsutaan ei-Bayes. Näin usein lopputulos tapahtuu kokeen toistuvien juoksujen aikana. Se on objektiivinen näkemys siitä, onko kokeilu toistettavissa.
Bayesilainen hypoteesitestaus on subjektiivinen näkemys samasta asiasta., Siinä otetaan huomioon, miten paljon uskot tuloksiisi. Toisin sanoen, panostaisitko rahaa kokeilusi lopputulokseen?
Erot Perinteisen ja Bayes-Hypoteesin Testaus.
perinteinen testaus (ei Bayesilainen) vaatii toistamaan näytteenottoa yhä uudelleen, kun taas Bayesilainen testaus ei. Suurin ero näiden kahden välillä on testauksen ensimmäisessä vaiheessa: todennäköisyysmallin ilmoittaminen. Bayesilaisessa testauksessa lisätään tähän vaiheeseen ennakkotietoa., Se edellyttää myös posteriorisen todennäköisyyden käyttöä,joka on satunnaiselle tapahtumalle annettu ehdollinen todennäköisyys, Kun kaikki todisteet katsotaan.
argumentit Bayesilaiselle testaukselle.
monien tutkijoiden mielestä se on parempi vaihtoehto perinteiselle testaukselle, koska se:
- Sisältää ennakkotietoa aineistosta.
- huomioi henkilökohtaiset uskomukset tuloksista.
argumentit vastaan.
- ennakkotietojen tai-tietojen sisällyttäminen ei ole perusteltua.
- on vaikea laskea verrattuna ei-Bayesilaiseen testaukseen.,
Takaisin alkuun
Hypoteesin Testaus Artikkeleita
Perusteet:
- Mitä on Ad Hoc-Testaus?
- Komposiittihypoteesikoe
- mikä on Hylkimisalue?
- mikä on Kaksipyrstökoe?
- miten päätetään, onko Hypoteesitesti Yksipyrstökoe vai Kaksipyrstökoe.
- miten päätetään, onko hypoteesi vasemmanpuoleinen vai Oikeapyrstöinen testi.
- miten tilastoissa ilmoitetaan nollahypoteesi.
- kuinka löytää kriittinen arvo.
- Miten Tukea tai Hylätä nollahypoteesi.,
Erityisiä Testejä:
- ANOVA.
- Brunner Munzel Testi (Generalized Wilcoxon-Testi)
- Chi-Square Testi Normaaliuden
- Cochran-Mantel-Haenszel-Testi
- F-Testi
- Grangerin Kausaliteetti-Testissä.
- Hotellingin T-neliö
- KPSS-testi.
- mikä on Todennäköisyystesti?
- Log rank-testi.
- MANCOVA
- Peräkkäistä Todennäköisyydellä Suhde Testi
- Miten Ajaa Sign-Testi.
- t testi: yksi näyte.
- t-testi: kaksi näytettä.
- Welchin ANOVA.
- Welchin testi epätasa-arvoisille Variansseille.,
- Z-testi: yksi näyte.
- Z-testi: kaksi osuutta
- Wald-testi.
- Mitä on Hyväksymis-Alueella?
- miten Chebyshevin lause lasketaan.
- Ratkaisusääntö.
- vapausasteet.
- Suunnattu Testi
- False Discovery Rate
- Miten laskea Ainakin Merkittävää Eroa.
- tasot tilastoissa.
- virhemarginaalin laskeminen.
- keskimääräinen ero (keskiarvojen ero)
- moninkertainen Testiongelma.
- mikä on Neyman-Pearson Lemma?
- yhden näytteen Mediaanitesti.,
- REGWF
- Miten Löytää otoskoko (Yleiset Ohjeet).
- Sig 2 (Tailed) eli tuloksissa
- mikä on standardoitu Testitilasto?
- Miten löytää standardivirhe
- standardoidut arvot: esimerkki.
- miten T-pisteet lasketaan.
- t-Score Vs. A Z. Score.
- testataan yhtä keskiarvoa.
- epätasa-arvoiset otoskoot.
- tasaisen tehokkaimmat testit.
- miten Z-pisteet lasketaan.
——————————————————————————
Tarvitsetko apua läksyjä tai testi kysymys?, Chegg-tutkimuksen avulla voit saada askel-askeleelta ratkaisuja kysymyksiisi alan asiantuntijalta. Ensimmäiset 30 minuuttia Chegg tutor on ilmainen!