Hypotese-Test
hovedformålet med statistikken er at afprøve en hypotese. For eksempel kan du køre et eksperiment og finde ud af, at et bestemt lægemiddel er effektivt til behandling af hovedpine. Men hvis du ikke kan gentage dette eksperiment, vil ingen tage dine resultater alvorligt. Et godt eksempel på dette var cold fusion discovery, der kørte ind i uklarhed, fordi ingen var i stand til at duplikere resultaterne.,
se videoen for en kort oversigt over hypotesetest, eller læs videre nedenfor:
indhold (Klik for at springe til sektionen):
- hvad er en hypotese?
- hvad er hypotesetest?
- hypotese test eksempler (En prøve Z Test).
- hypotese Test på en gennemsnitlig (TI 83).
- Bayesian hypotese test.
- Mere Hypotesetest Artikler
Se også:
- Hypotese-Test i Ét Billede
- Kritiske Værdier
- Hvad er Null-Hypotese?,
brug for hjælp til et hjemmearbejde problem? Tjek vores vejledning side!
Hvad er en Hypotese?
Andreas Cellarius hypotese, der viser planeternes bevægelser.
En hypotese er et uddannet gæt om noget i verden omkring dig. Det skal være testbart, enten ved forsøg eller observation. For eksempel:
- en ny medicin, du tror kan virke.
- en måde at undervise på, kan være bedre.,
- en mulig placering af nye arter.
- en mere retfærdig måde at administrere standardiserede tests på.
det kan virkelig være noget som helst, så længe du kan sætte det på prøve.
Hvad er en hypotese Erklæring?
Hvis du vil foreslå en hypotese, er det sædvanligt at skrive en erklæring. Din erklæring vil se sådan ud:
“Hvis jeg…(gør dette til en uafhængig variabel)….derefter (dette vil ske med den afhængige variabel).”
For eksempel:
- hvis jeg (reducer mængden af vand, der gives til urter) derefter (urterne vil stige i størrelse).,
- hvis jeg (giver patienter rådgivning ud over medicin) derefter (deres samlede depression skala vil falde).
- hvis jeg (giver eksamener ved middagstid i stedet for 7) derefter (studerendes testresultater forbedres).
- hvis jeg (se på dette bestemte sted) så (jeg er mere tilbøjelig til at finde nye arter).
en god hypoteseopgørelse skal:
- indeholde en “hvis” og “derefter” erklæring (ifølge University of California).
- omfatter både de uafhængige og afhængige variabler.
- kan testes ved forsøg, undersøgelse eller anden videnskabeligt forsvarlig teknik.,
- være baseret på oplysninger i tidligere forskning (enten din eller en andens).
- har designkriterier (for ingeniør-eller programmeringsprojekter).
Hvad er hypotesetest?
hypotesetest i statistik er en måde for dig at teste resultaterne af en undersøgelse eller et eksperiment for at se, om du har meningsfulde resultater. Du tester dybest set, om dine resultater er gyldige ved at finde ud af oddsene for, at dine resultater er sket ved en tilfældighed., Hvis dine resultater kan være sket ved en tilfældighed, eksperimentet vil ikke være gentagelig og så har lidt brug. hypotesetest kan være et af de mest forvirrende aspekter for studerende, mest fordi før du endda kan udføre en test, skal du vide, hvad din nulhypotese er. Ofte kan disse vanskelige ordproblemer, som du står over for, være vanskelige at dechiffrere., Men det er nemmere end du tror, alt hvad du behøver gøre, er:
- Figur ud din nulhypotesen,
- oplyse dit nulhypotesen,
- Vælg, hvilken slags prøve du har brug for til at udføre,
- Enten støtte eller forkaste nulhypotesen.
Hvad er nulhypotesen?
Hvis du sporer videnskabens historie, er nulhypotesen altid den accepterede kendsgerning. Enkle eksempler på nulhypoteser, der generelt accepteres som sande, er:
- DNA er formet som en dobbelt Heli..
- der er 8 planeter i solsystemet (undtagen Pluto).,
- hvis du tager Vio.., kan du øge risikoen for hjerteproblemer (et lægemiddel, der nu er taget ud af markedet).
hvordan angiver jeg nulhypotesen?
du bliver ikke forpligtet til faktisk at udføre et rigtigt eksperiment eller undersøgelse i elementær statistik (eller endda modbevise en kendsgerning som “Pluto er en planet”!), så du får ordproblemer fra virkelige situationer. Du bliver nødt til at finde ud af, hvad din hypotese er fra problemet. Dette kan være lidt vanskeligere end bare at finde ud af, hvad den accepterede kendsgerning er. Med ordproblemer søger du at finde en kendsgerning, der er nullificerbar (dvs., noget du kan afvise).
Hypotesetest Eksempler #1: Grundlæggende Eksempel
En forsker mener, at hvis knæet kirurgi patienter går til fysioterapi to gange om ugen (i stedet for 3 gange), deres recovery periode bliver længere. Gennemsnitlige gendannelsestider for knæoperationspatienter er 8, 2 uger.
Den hypotese erklæring i dette spørgsmål er, at forskeren mener, at den gennemsnitlige recovery tid er mere end 8.2 uger. Det kan skrives i matematiske termer som:
H1:
Dernæst skal du angive nulhypotesen (se: sådan angives nulhypotesen). Det er, hvad der vil ske, hvis forskeren er forkert. I ovenstående eksempel, hvis forskeren er forkert, er gendannelsestiden mindre end eller lig med 8, 2 uger. I matematik, der er:
H0 μ ≤ 8.2
Afvisning af nulhypotesen
Ti år eller så siden, troede vi, at der var 9 planeter i solsystemet. Pluto blev nedlagt som en planet i 2006. Nullhypotesen om “Pluto er en planet” blev erstattet af “Pluto er ikke en planet.,”Selvfølgelig er afvisning af nulhypotesen ikke altid så let-den hårde del er normalt at finde ud af, hvad din nulhypotese er i første omgang.
Hypotesetesteksempler (en prøve Test-Test)
den ene prøve test-test bruges ikke meget ofte (fordi vi sjældent kender den faktiske populationsstandardafvigelse). Det er dog en god ide at forstå, hvordan det fungerer, da det er en af de enkleste tests, du kan udføre i hypotesetest., I engelsk klasse skal du lære det grundlæggende (som grammatik og stavemåde), før du kunne skrive en historie; tænk på en prøve z-test som grundlaget for at forstå mere kompleks hypotesetest. Denne side indeholder to hypotese test eksempler på en prøve z-test.
eksempler på hypotesetest: #2
En rektor på en bestemt skole hævder, at eleverne i hans skole er over gennemsnittet intelligens. En tilfældig prøve på tredive studerende i. – score har en gennemsnitlig score på 112., Er der tilstrækkelige beviser til at støtte rektorens påstand? Den gennemsnitlige befolkning i I er 100 med en standardafvigelse på 15. trin 1: Angiv nulhypotesen. Den accepterede kendsgerning er, at befolkningen betyder 100, så: H0: μ=100. Trin 2: Angiv den alternative hypotese. Påstanden er, at eleverne har over gennemsnittet i. – score, så:
H1: det faktum, at vi leder efter scoringer “større end” et bestemt punkt betyder, at dette er en one-tailed test. Trin 3: Tegn et billede for at hjælpe dig med at visualisere problemet.,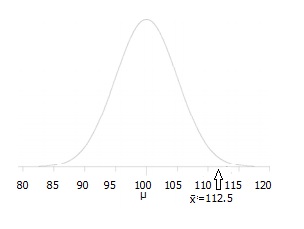
Trin 4: Angiv alfa-niveauet. Hvis du ikke får et alfa-niveau, skal du bruge 5% (0,05).
Trin 5: Find afvisningsregionens område (givet af dit alfaniveau ovenfor) fra table-tabellen. Et område af .05 er lig med en 1.6-score på 1.645. trin 6: Find teststatistikken ved hjælp af denne formel: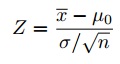 
For dette datasæt: (112.5 – 100) / (15/√30) = 4.56. trin 6: hvis Trin 6 er større end Trin 5, skal du afvise nulhypotesen., Hvis det er mindre end Trin 5, kan du ikke afvise nulhypotesen. I dette tilfælde er det større (4,56 > 1.645), så du kan afvise null.
eksempler på hypotesetest: #3
blodglukoseniveauer for overvægtige patienter har et gennemsnit på 100 med en standardafvigelse på 15. En forsker mener, at en diæt, der er høj i rå majsstivelse, vil have en positiv eller negativ effekt på blodsukkerniveauet., En prøve på 30 patienter, der har prøvet den rå majsstivelse diæt, har et gennemsnitligt glukoseniveau på 140. Test hypotesen om, at den rå majsstivelse havde en effekt.
*denne proces gøres meget lettere, hvis du bruger en TI-83 eller e .cel til at beregne z-score (den “kritiske værdi”).,
Se:
- Kritisk z-værdi TI 83
- Z-Score i Excel
Hypotesetest Eksempler: Mean (ved Hjælp af TI-83)
Du kan bruge TI-83 lommeregner til hypotesetest, men regnemaskinen ikke finde ud af null og alternative hypoteser; det er op til dig at læse spørgsmålet og skrive det i programmet.
Eksempel problem: en stikprøve på 200 personer har en gennemsnitlig alder på 21 med en population standardafvigelse (σ) på 5. Test hypotesen om, at befolkningens gennemsnit er 18, 9 Ved α = 0, 05.Trin 1: Angiv nulhypotesen., I dette tilfælde er nulhypotesen, at befolkningstallet er 18,9, så vi skriver:
H0: = = 18,9
Trin 2: Angiv den alternative hypotese. Vi ønsker at vide, hvis vores stikprøve, som har et gennemsnit på 21 i stedet for 18.9, der virkelig er forskellige fra befolkningen, derfor er vores alternative hypotese:
H1: μ ≠ 18.9
Trin 3: Tryk på Stat og tryk derefter på højre pil for to gange for at vælge TESTS.Trin 4: Tryk på 1 For at vælge 1:Test-Test…. Tryk på ENTER.Trin 5: Brug Højre pil til at vælge statistik.Trin 6: indtast dataene fra problemet:
00: 18.,9
σ: 5
.: 21
n: 200
μ :000
Trin 7: pil ned for at beregne, og tryk på ENTER. Lommeregneren viser p-værdien:
p = 2,87 .10-9
Dette er mindre end vores alfa-værdi af.05. Det betyder, at vi bør afvise nulhypotesen.
Bayesian hypotese test: Hvad er det?
Billede: Los Alamos National Lab.Bayesian hypotese test hjælper med at besvare spørgsmålet: kan resultaterne fra en test eller undersøgelse gentages?
Hvorfor er vi ligeglade med, om en test kan gentages?, Lad os sige, at tyve mennesker i samme landsby kom ned med leukæmi. En gruppe forskere finder ud af, at mobiltelefontårne har skylden. En anden undersøgelse fandt imidlertid, at mobiltelefontårne ikke havde noget at gøre med kræftklyngen i landsbyen. Faktisk fandt de, at cancers var helt tilfældige. Hvis det lyder umuligt, kan det faktisk ske! Klynger af kræft kan ske ved en tilfældighed. Der kan være mange grunde til, at den første undersøgelse var defekt., En af hovedårsagerne kunne være, at de bare ikke tog højde for, at nogle gange sker ting tilfældigt, og vi ved bare ikke hvorfor.
P værdier.
det er god videnskab at fortælle folk, om dine undersøgelsesresultater er solide, eller om de kunne være sket ved en tilfældighed. Den sædvanlige måde at gøre dette på er at teste dine resultater med en p-værdi. En p-værdi er et tal, som du får ved at køre en hypotesetest på dine data. En p-værdi på 0,05 (5%) eller mindre er normalt nok til at hævde, at dine resultater kan gentages., Der er dog en anden måde at teste gyldigheden af dine resultater på: Bayesian hypotese test. Denne type test giver dig en anden måde at teste styrken af dine resultater.
Bayesian hypotese test.
traditionel test (den type, du sandsynligvis stødte på i elementær statistik eller AP-statistik) kaldes ikke-Bayesian. Det er, hvor ofte et resultat sker i løbet af gentagne kørsler af eksperimentet. Det er et objektivt billede af, om et eksperiment kan gentages.
Bayesian hypotese test er en subjektiv opfattelse af det samme., Det tager højde for, hvor meget tro du har på dine resultater. Med andre ord, vil du satse penge på resultatet af dit eksperiment?
forskelle mellem traditionel og Bayesian hypotese test.
traditionel test (ikke Bayesian) kræver, at du gentager prøveudtagning igen og igen, mens Bayesian test ikke gør det. Den vigtigste forskel mellem de to er i det første trin i testen: angivelse af en sandsynlighedsmodel. I Bayesian testing tilføjer du forudgående viden til dette trin., Det kræver også brug af en posterior sandsynlighed, hvilket er den betingede sandsynlighed, der gives til en tilfældig begivenhed, efter at alle beviser er overvejet.
argumenter for Bayesian test.
mange forskere mener, at det er et bedre alternativ til traditionel test, fordi det:
- indeholder forudgående viden om dataene.
- tager hensyn til personlige overbevisninger om resultaterne.
argumenter imod.
- herunder tidligere data eller viden er ikke berettiget.
- det er vanskeligt at beregne sammenlignet med ikke-bayesisk test.,
Tilbage til toppen
hypotesetest artikler
grundlæggende:
- hvad er Ad Hoc-test?
- Composite Hypothesis Test
- hvad er en Afvisningsregion?
- hvad er en to-Tailed Test?
- hvordan man beslutter, om en hypotesetest er en en-Tailed Test eller en to-Tailed Test.
- hvordan man beslutter, om en hypotese er en venstre Tailed Test eller en Right-Tailed Test.
- sådan angives nulhypotesen i statistikker.
- Sådan finder du en kritisk værdi.
- sådan understøttes eller afvises en Nulhypotese.,
specifikke Tests:
- ANOVA.
- Brunner Munzel Test (Generaliseret Wilcoxon Test)
- Chi Square Test for Normalitet
- Cochran-Mantel-Haenszel Test
- F-Test
- Granger Kausalitet Test.
- Hotelling ‘ S T-S KPUARED
- KPSS Test.
- hvad er en Sandsynlighedsforholdstest?
- Log rank test.
- Mancova
- sekventiel Sandsynlighedsforholdstest
- Sådan køres en Tegntest.
- t Test: en prøve.
- T-Test: to prøve.
- Welelchs ANOVA.
- Welelchs Test for ulige afvigelser.,
- Test-Test: en prøve.
- Test Test: to forhold
- Testald Test.
- hvad er en accept Region?
- Sådan beregnes Chebyshevs sætning.
- afgørelse regel.
- grader af frihed.
- Retningstest
- falsk Opdagelsesfrekvens
- Sådan beregnes den mindst signifikante forskel.
- niveauer i statistik.
- Sådan beregnes fejlmargen.
- Middelforskel (forskel i midler)
- det Multiple Testproblem.
- hvad er Neyman-Pearson Lemma?
- en prøve Median Test.,
- REG .f
- Sådan finder du en prøvestørrelse (generelle instruktioner).
- Sig 2 (Tailed) betydning i resultater
- hvad er en standardiseret teststatistik?
- Sådan finder du standardfejl
- standardiserede værdier: eksempel.
- Sådan beregnes en T-Score.
- T-Score Vs. A Score. Score.
- test af en enkelt middelværdi.
- ulige stikprøvestørrelser.
- ensartet mest kraftfulde Tests.
- Sådan beregnes en Score-Score.
> ——————————————————————————
har du Brug for hjælp med lektier eller spørgsmål til test?, Med Chegg Study kan du få trinvise løsninger på dine spørgsmål fra en ekspert på området. Din første 30 minutter med en Chegg tutor er gratis!