The colors of the body of the table illustrate the number of ways to throw each total., Sandsynligheden for at kaste en given total er antallet af måder at kaste den samlede divideret med det samlede antal kombinationer (36). I den følgende tabel vises det specifikke antal måder at kaste hver total på og sandsynligheden for at kaste den samlede mængde.

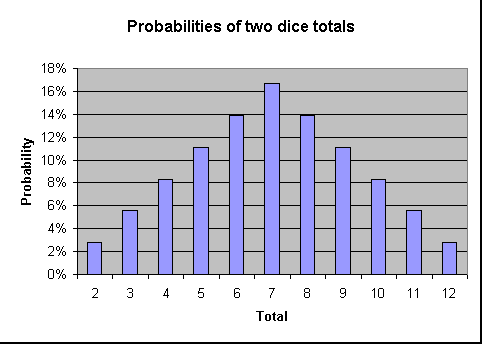
Følgende viser sandsynligheden for at kaste hver total i et diagram format. Som diagrammet viser jo tættere den samlede er til 7 jo større er sandsynligheden for det bliver kastet.,

Field Bet Eksempel

Nu, at vi forstår, at sandsynligheden for at kaste hver samlede vi kan anvende disse oplysninger til de terninger spil i kasinoer til at beregne hus kant. For eksempel overveje feltet bet i craps. Dette spil betaler 1: 1 (lige penge), hvis det næste kast er en 3, 4, 9, 10 eller 11, 2:1 (fordoble indsatsen) på 2, og 3:1 (tredobbelt indsatsen) på 12. Bemærk, at der er 7 totaler, der vinder og kun 4, der taber, hvilket kan forårsage nogen, der ikke vidste bedre at tro, at det var en god gamble.,

spillerens afkast kan defineres som summen af produkterne af sandsynligheden for hver begivenhed og nettoafkastet af denne begivenhed. Følgende tabel viser hver mulig total, nettoafkastet, sandsynligheden for at kaste det samlede beløb og det gennemsnitlige afkast. Det gennemsnitlige afkast er produktet af nettoafkastet og sandsynligheden. Spillerens afkast er summen af det gennemsnitlige afkast.

den sidste række viser spillerens tilbagevenden til at være -.0278, med andre ord for hver $1 bet spilleren kan forvente at tabe 2,78 cent., Spillerens tab er husets gevinst, så huskanten er produktet af -1 og spillerens afkast, i dette tilfælde 0,0278 eller 2,78%.

for sandsynlighederne i summen af mere end to terninger se venligst mine sandsynligheder for 1 til 25 terninger sektion.

skrevet af: Michael Shackleford