• Historiske Baggrund
• Tilsyneladende Størrelsesklasse, m
• Absolutte Størrelse, M
• at Finde Afstanden til Stjerner – Afstand Modul
• Størrelse/Distance Beregninger
• Navngivning & Identificere Stjerner

Undersøgelse star felt fotografi, der er vist nedenfor. Det viser et område af himlen omkring stjernebilledet Cru., ofte kaldet Sydkorset. Flyt markøren hen over billedet for at identificere nogle stjerner.

hvilken stjerne er lyseste?,

Hvis du svarede Alpha (cent) Centauri, stjernen nederst til venstre på fotografiet du har ret. Som du kan se, viser et fotografisk billede som dette mange flere stjerner, end du kan se med dit blotte øje. Ikke desto mindre er nogle stjerner mere fremtrædende end andre. Ved at vælge cent Centauri lavede du nogle antagelser. Hvad var de? et fotografi som dette viser klare stjerner som større diske end svagere stjerner., Betyder det, at disse stjerner er fysisk større end de svagere stjerner på billedet? Husk, i afsnittet om astrometri lærte vi, at alle andre stjerner end vores Sol er så fjerne, at de effektivt er punktkilder. Hvorfor ser nogle så lysere ud (for vores øjne) eller større (på fotografier) end andre? Hvad er faktisk lysstyrke, og hvordan kan vi måle det? Svarene på disse spørgsmål danner fokus for dette afsnit.,

Historiske Baggrund

begrebet måling og sammenligning af lysstyrken af stjerner, der kan spores tilbage til den græske astronom og matematiker Hipparchus (190 – 120 F.KR.). En af de største astronomer i antikken, han er krediteret med at producere et katalog af 850 stjerner med positioner og sammenlignende lysstyrker., I hans system blev de lyseste stjerner tildelt en størrelse på 1, Den næste lyseste Størrelse 2 og så videre til de svageste stjerner, bare synlige for det blotte øje, som var Størrelse 6. Denne seks-punkts skala kan betragtes som en placering, førsteklasses stjerner, de lyseste, var første størrelse, og svage lavhastighedsstjerner var sjette størrelse.

opdagelsen af svagere stjerner med teleskoper i begyndelsen af 1600-tallet krævede, at skalaen blev udvidet ud over størrelsen 6., Udviklingen af visuelle fotometre, instrumenter til måling af stjerneintensiteter i det nittende århundrede af John Herschel og andre fik astronomerne til at vedtage en international standard. Det faktum, at øjnene påvise forskelle i intensitet logarithmically snarere end lineært blev opdaget i 1830’erne. I 1856 Norman Pogson foreslået, at en stjerne af størrelsesorden 1 var 100 × lysere end en stjerne af størrelsesorden 6. En forskel på en størrelse var derfor lig med 5 100 100 = 2, 512 gange i lysstyrke.,

tilsyneladende størrelse, M

den tilsyneladende størrelse, m, af en stjerne er den størrelse, den har set af en observatør på jorden.

et meget lyst objekt, såsom solen eller månen, kan have en negativ tilsyneladende størrelse. Selvom Hipparchus oprindeligt tildelte de lyseste stjerner til at have en størrelse på 1 mere omhyggelig sammenligning viser, at den lyseste stjerne på nattehimlen, Sirius eller can Canis Majoris (CMa) faktisk har en tilsyneladende størrelse på m = -1.44. Med omkalibreringen af Hipparchus ‘ oprindelige værdier er den klare stjerne Vega nu defineret til at have en tilsyneladende størrelse på 0,0.,

efter den teleskopiske opdagelse af svage stjerner i begyndelsen af 1600-tallet har størrelsesskalaen også været nødt til at udvides til objekter svagere end størrelsesorden 6. Tabellen nedenfor viser rækkevidden af tilsyneladende størrelser for himmelobjekter.

Objektet	Tilsyneladende Størrelse
Sol	-26.5
fuldmåne	-12.5
Venus	-4.,3
Mars or Jupiter	-2
Sirius (α CMa)	-1.44
Vega (α Lyr)	0.0
Alnair (α Gru)	1.73
Naked-eye limit	6.5
Binocular limit	10
Proxima Cen	11.,09
Visual limit through 20 cm telescope	14
QSO at redshift z = 2	≈ 20
Cepheid in galaxy M100 observed with HST	26
Galaxy at z = 6 observed with Gemini 8.1 m telescope	28
Limit for James Webb Space Telescope	≥ 30

If a star of magnitude 1 is 2.,512 × lysere end en stjerne af størrelsesorden 2 og 100 &gange lysere end en sjettedel størrelsesorden stjerne, hvor meget lysere er det end en stjerne i størrelsesorden 3? Du skal være forsigtig her. Det er ikke blot 2 2 2.512 anderledes. Du skal huske, at en forskel på en størrelse er lig med 5 100 100 = 2,512. En forskel på 2 størrelser derfor = 2,5122 = 6,31 difference forskel i lysstyrke.

to objekter med forskellige størrelser varierer derfor i lysstyrke med 2.512 hævet til kraften i din størrelsesforskel., Hvis vi skriver dette som en ligning, forholdet mellem lysstyrken eller intensitet, IA/IB mellem to objekter, A og B, med størrelser mA og mB er givet ved følgende ligning:

Lad os se på et eksempel.eksempel 1: sammenligning af to stjerner.
Hvor meget lysere er Alnair, tilsyneladende størrelsesklasse på +1.73 end Proxima Cen med en størrelse på 11.09?
ved Hjælp af ligning 4.1 har vi:

så, som optræder i:

Eksempel 2: Hvor meget lysere er Solen end fuldmånen?
for dette husker vi fra tabellen ovenfor, at Solen har en tilsyneladende størrelse på -26,5 og fuldmåne, – 12,5.

Så ved hjælp af ligning 4.1 får vi:

som optræder i giver os:

det er vigtigt at huske, at størrelsen simpelthen er et tal, det har ingen enheder. Symbolet for tilsyneladende størrelse er et lille bogstav m; Du skal gøre dette klart i ethvert problem.

Absolutte Størrelsesklasse, M

Hvad betyder det faktum, at Sirius har en tilsyneladende størrelsesklasse på -1.44 og Betelgeuse en tilsyneladende størrelsesklasse på 0,45 fortælle os om disse to stjerner? En anden måde at tænke på dette er at spørge, hvorfor er Sirius den lyseste stjerne på nattehimlen?, En stjerne kan ses lyse, for to hovedårsager:

1. Det kan være uløseligt lysende, er, at det kan være en stærk kilde til emission af elektromagnetisk stråling, eller
2. Det kan være meget tæt på os, eller begge dele.

den tilsyneladende størrelse af en stjerne afhænger derfor delvis af dens afstand fra os. Faktisk ser Sirius lysere ud end Betelgeuse netop fordi Sirius er meget tæt på os, kun 2.6 pc væk, mens Betelgeuse er omkring 160 pc fjernt., Erkendelsen af, at Stjerner ikke alle har meget den samme lysstyrke, betød, at tilsyneladende størrelse alene ikke var tilstrækkelig til at sammenligne stjerner. Et nyt system, der ville give astronomer mulighed for direkte at sammenligne stjerner, blev udviklet. Dette system kaldes det absolutte størrelse, M.

Den absolutte størrelsesklasse, M, af en stjerne er i den størrelsesorden, som stjernen ville have hvis den var i en afstand af 10 parsec fra os. En afstand på 10 pc er rent vilkårlig, men nu internationalt aftalt af astronomer., Skalaen for absolut størrelsesorden er den samme som for tilsyneladende størrelsesorden, der er en forskel på 1 størrelsesorden = 2,512 gange forskel i lysstyrke. Denne logaritmiske skala er også åben og unitless. Igen, jo lavere eller mere negativ værdien af M, jo lysere er stjernen. Absolut størrelse er en bekvem måde at udtrykke en stjernes lysstyrke på. Når den absolutte størrelse af en stjerne er kendt, kan du også sammenligne den med andre stjerner. Betelgeuse, m = -5.6 er i sig selv mere lysende end Sirius med en m = 1.41.

vores sol har en absolut visuel størrelse på 4,8.,

find afstanden til stjerner – Afstandsmodul

som du måske husker fra afsnittet om astrometri, er de fleste stjerner for fjerne til at få deres paralla.målt direkte. Ikke desto mindre, hvis du kender både de tilsyneladende og absolutte størrelser for en stjerne, kan du bestemme dens afstand. Lad os se igen på Sirius og Betelgeuse plus en anden stjerne kaldet GJ 75.

hvor langt væk er GJ 75? Det er en usædvanlig stjerne, idet dens tilsyneladende og absolutte størrelser er de samme. Hvorfor? Årsagen er, at det faktisk er 10 parsecs fjernt fra os, så per definition skal dens to størrelser være de samme.,

hvad med Sirius? Dens tilsyneladende størrelse er lavere (derfor lysere) end dens absolutte størrelse. Det betyder, at det er tættere end 10 parsecs til os. Betelgeuses tilsyneladende størrelse er højere (derfor lysere) end dens absolutte størrelse, så det ser ud til at være endnu lysere på nattehimlen, hvis det kun var 10 parsecs fjernt.

astronomer bruger forskellen mellem tilsyneladende og absolut størrelse, afstandsmodulet, som en måde at bestemme afstanden til en stjerne på.

• Distance Modulus = m – M.
• Distance modulus er negativt for stjerner tættere end 10 parsecs.,
• Afstandsmodul er positivt for stjerner længere væk end 10 parsecs.
• størrelsen på afstandsmodulet bestemmer den faktiske værdi af afstanden, så en stjerne med afstandsmodul 1.5 er tættere end en med et afstandsmodul på 8.7.

Størrelse/Distance Beregninger

Den afstand modul kan bruges til at bestemme afstanden til en stjerne ved hjælp af ligningen:

hvor d er i parsec. Bemærk, at hvis d = 10 pc derefter m og M er de samme. (En formel afledning af denne ligning er givet på Næste side om lysstyrke)., NS.HSC pensum Formula Sheet giver ligningen som:

men dette er simpelthen en omarbejdning af ligning 4.2. Du skal være komfortabel med at løse denne ligning givet to af de tre variabler. Lad os vide se på, hvordan du kan løse nogle eksempler.eksempel 3: givet m og d, nødt til at finde M.
β Crucis (eller Mimosa) har en tilsyneladende størrelse på 1,25 og er 108 parsecs fjernt. Hvad er dens absolutte størrelse?under anvendelse af ligning 4.3 har vi:

så β Crucis har en absolut størrelsesklasse på -3.92
Bemærk denne beregning har vist, fuld arbejdstid, således at hvert trin er eksplicit. (Husk at løse størrelsesligninger log henviser til logaritmer til base 10 og ikke naturlige logaritmer eller ln.eksempel 4: givet m og M, find d.
Betelgeuse har en tilsyneladende størrelse på 0,45 og en absolut størrelse på -5,14. Hvor langt væk er det?
dette problem kræver, at vi omskriver ligning 4.2 for at give os d som det ukendte., Dette er vist nedenfor:

, som kan skrives som:

nu optræder i:

så Betelgeuse er omkring 130 pc fjern.

igen viser dette eksempel fuldstændig arbejde, mens du i virkeligheden muligvis ikke viser hvert trin., Det er dog vigtigt, at du indstiller dit arbejde til sådanne problemer klart, så du kan tjekke din algebraiske manipulation og dine substitutioner. Det kan være vanskeligt at arbejde med logfiler og indekser, så sørg for, at du ved, hvordan du gør disse på din lommeregner.

Eksempel 5: I M og d, finde m.
I praksis er denne type af problemet er mindre realistisk for faktiske objekter, som vi normalt kan måle deres tilsyneladende størrelser direkte, men det kan være at vi ønsker at beregne, hvad der tilsyneladende størrelsesklasse en klasse eller type af objekt kan have givet de andre parametre. Igen, begyndende med ligning 4.,3 Lad os bestemme, hvor lyst en supergiant som Deneb med en absolut størrelse på -8.73 ville se ud, hvis den var 230 parsecs væk.

så erstatte i:

så Deneb ville have en tilsyneladende størrelsesklasse på -1.89. Dette ville gøre det lysere på vores nattehimmel end Sirius (m = -1.44)., I virkeligheden er Deneb omkring 990 pc fjernt, selvom denne værdi har en stor usikkerhed.eksempel 6: Hvad hvis d ikke er givet, men paralla?, p er givet?dette er faktisk meget ligetil. Husk fra afsnittet om astrometri, at der er et direkte forhold mellem afstand og paralla..

så du skal blot indsætte dette i ligning 4.2 eller 4.3.

navngivning& identificerende stjerner

lad os vide gense det billede af Cru.og pegerne fra toppen af denne side., Billedet nedenfor viser det samme område med de fremtrædende stjerner mærket. De har også deres tilsyneladende størrelser vist. CRU.er en konstellation, en af 88 regioner, som den himmelske sfære er blevet brudt op i og aftalt internationalt af astronomer. CRU.er faktisk den mindste af konstellationerne og er let identificeret i de sydlige himmel. De fremtrædende nærliggende stjerner, der ofte kaldes pegerne, er faktisk en del af en stor konstellation kaldet Centaurus.

Nu kan du opleve, at stjernerne er navngivet med bogstaver fra det græske alfabet; α, β, γ δ og ε (alpha, beta, gamma, delta, epsilon, der bliver de fem første) efterfulgt af standard forkortelse på tre bogstaver for hver konstellation (Cru for Crucis eller Kernen og Cen for Centaurus). Hvis du ser nøje på de tilsyneladende størrelser for de fem navngivne stjerner i Cru., vil du se, at den lyseste stjerne er mærket α, Den næste β og så videre., Dette system kaldes Bayer-systemet, efter Johann Bayer, der introducerede det i 1603. Den lyseste stjerne i en konstellation er tildelt bogstavet A, Den næste β og så videre. En undtagelse fra denne regel er &alpha Orionis eller Betelgeuse. Det er faktisk svagere end β Ori, Rigel med en lille mængde. Dette er en interessant historisk sag løst ved Erkendelsen af, at Betelgeuse er dæmpet lidt i lysstyrke, siden den blev navngivet under Bayer-systemet.,

et punkt at huske om konstellationer er, at stjernerne i en konstellation normalt ikke er fysisk forbundet med hinanden, i modsætning til stjerner i klynger. Det faktum, at vises tæt sammen er rent en justering effekt langs tour linje af syne. Faktisk er stjernerne i regionen ovenfor vidt adskilt i afstand fra os som vist på det næste billede.

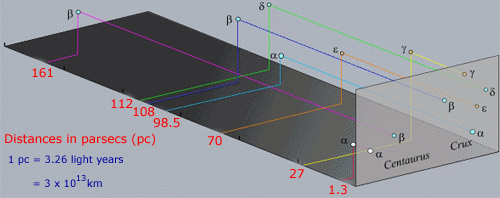
Nogle af de lyse stjerner som Cen Cen har også deres eget specifikke navn. Sirius (α Sco) er et af disse eksempler, mens Cen Cen også kaldes Rigel Kentaurus. Mange stjernenavne er arabisk oprindelse fra den æra, hvor græske optegnelser blev bevaret og udviklet af islamiske astronomer. Problemet med Bayer-systemet med navngivning af stjerner er, at der kun er 24 bogstaver i det græske alfabet, men der er mange flere stjerner end i hver konstellation. de fleste stjerner har faktisk ikke et bestemt navn eller Bayer-klassificering., I disse dage har astronomer samlet store kataloger over stjerner, nogle med over 10 millioner objekter, så de fleste stjerner har kun et katalognummer. Stjerner kan have mange mere end et identifikationsnavn eller katalognummer, afhængigt af antallet af kataloger, de er i. Den variable stjerne, δ Cep for eksempel er også kendt som HIP 110991, SAO 34508, eller nogen af mere end 30 andre identifikatorer! Mange kataloger udnytter himmelske koordinater såsom højre opstigning og deklination til at identificere objekter. Således δ Cep er kendt som IRAS 22273+5809, CCDM J22292+5825A og AAVSO 2225+57., De små variationer i RA og dec for katalogerne opstår på grund af stjernernes korrekte bevægelse og præcessionen af referencerammen.