Testování Hypotéz
 hlavním cílem statistiky je testování hypotéz. Můžete například provést experiment a zjistit, že určitý lék je účinný při léčbě bolesti hlavy. Ale pokud nemůžete tento experiment opakovat, nikdo nebude brát vaše výsledky vážně. Dobrým příkladem byl objev studené fúze, která vymizela do neznáma, protože nikdo nebyl schopen duplikovat výsledky.,
hlavním cílem statistiky je testování hypotéz. Můžete například provést experiment a zjistit, že určitý lék je účinný při léčbě bolesti hlavy. Ale pokud nemůžete tento experiment opakovat, nikdo nebude brát vaše výsledky vážně. Dobrým příkladem byl objev studené fúze, která vymizela do neznáma, protože nikdo nebyl schopen duplikovat výsledky.,
podívejte se na video pro stručný přehled testování hypotéz, nebo si přečtěte níže:
Obsah (kliknutím přeskočíte do sekce):
- co je hypotéza?
- co je testování hypotéz?
- příklady testování hypotéz (jeden vzorek z testu).
- test hypotézy na střední (TI 83).
- Bayesovské testování hypotéz.
- Více Testování Hypotéz Články
Viz také:
- Hypotéza Testy v Jednom Obrázku
- Kritické Hodnoty
- Co je Nulové Hypotézy?,
potřebujete pomoc s problémem s domácími úkoly? Podívejte se na naši stránku doučování!
co je hypotéza?

Andreas Cellarius hypotéza, ukazující planetární pohyby.
hypotéza je vzdělaný odhad o něčem ve světě kolem vás. Mělo by být testovatelné, buď experimentem nebo pozorováním. Například:
- nový lék, o kterém si myslíte, že by mohl fungovat.
- způsob výuky si myslíte, že by mohlo být lepší.,
- možné umístění nových druhů.
- spravedlivější způsob správy standardizovaných testů.
může to být opravdu cokoli, pokud to můžete vyzkoušet.
co je to tvrzení hypotézy?
Pokud se chystáte navrhnout hypotézu, je obvyklé napsat prohlášení. Vaše prohlášení bude vypadat takto:
“ Pokud … (udělejte to nezávislé proměnné)….pak (to se stane závislé proměnné).“
například:
- Když jsem (snižte množství vody dané byliny), pak (bylinky zvýší ve velikosti).,
- pokud I (poskytuji pacientům poradenství kromě léků), pak (jejich celková stupnice deprese se sníží).
- pokud (dávám zkoušky v poledne místo 7), pak (skóre studentských testů se zlepší).
- pokud (podívejte se na toto určité místo) pak (pravděpodobněji najdu nové druhy).
dobrá hypotéza by měla:
- obsahovat prohlášení“ if „a“ then “ (podle University of California).
- zahrnují nezávislé i závislé proměnné.
- být testovatelný experimentem, průzkumem nebo jinou vědecky zvukovou technikou.,
- být založen na informacích v předchozím výzkumu (buď vaše nebo někoho jiného).
- mají konstrukční kritéria (pro inženýrské nebo programovací projekty).
co je testování hypotéz?

testování Hypotéz ve statistice je způsob, jak pro vás otestovat výsledky průzkumu, nebo experiment, aby zjistili, zda máte smysluplné výsledky. V podstatě testujete, zda jsou vaše výsledky platné, když zjistíte, že vaše výsledky se staly náhodou., Pokud se vaše výsledky mohly stát náhodou, experiment nebude opakovatelný, a tak má jen málo využití.
testování hypotéz může být pro studenty jedním z nejvíce matoucích aspektů, hlavně proto, že než budete moci dokonce provést test, musíte vědět, jaká je vaše nulová hypotéza. Často ty složité problémy se slovem, kterým čelíte, mohou být obtížné dešifrovat., Ale je to jednodušší, než si myslíte. vše, co musíte udělat, je:
- Zjistit vaše nulovou hypotézu,
- uveďte své nulovou hypotézu,
- Vyberte si, jaký druh testu je třeba provést,
- Buď podpořit nebo odmítnout nulovou hypotézu.
jaká je nulová hypotéza?
Pokud vysledujete historii vědy, nulová hypotéza je vždy akceptovanou skutečností. Jednoduché příklady null hypotéz, které jsou obecně přijímány jako pravdivé, jsou:
- DNA ve tvaru dvojité šroubovice.
- ve sluneční soustavě je 8 planet (kromě Pluta).,
- užívání přípravku Vioxx může zvýšit riziko srdečních problémů (lék nyní odebraný z trhu).
Jak mohu uvést nulovou hypotézu?
nebudete muset skutečně provádět skutečný experiment nebo průzkum v elementárních statistikách (nebo dokonce vyvrátit skutečnost, jako je „Pluto je planeta“!), takže budete mít slovo problémy z reálných situacích. Budete muset zjistit, jaká je vaše hypotéza z problému. To může být trochu složitější, než jen přijít na to, co je přijatou skutečností. S problémy se slovem, hledáte najít fakt, který je nullifiable (tj., něco, co můžete odmítnout).
Testování Hypotéz Příklady #1: Základní Příklad
výzkumník si myslí, že pokud operaci kolena pacienti jít do fyzikální terapie dvakrát týdně (namísto 3 krát), jejich rekonvalescence bude delší. Průměrná doba zotavení pacientů s operací kolena je 8,2 týdnů.
hypotéza prohlášení v této otázce je to, že výzkumník se domnívá, průměrná doba zotavení je více než 8,2 týdnů. Může být napsán matematicky jako:
H1: μ > 8.,2
Dále budete muset uvést nulovou hypotézu (viz: Jak uvést nulovou hypotézu). To se stane, pokud se výzkumník mýlí. Ve výše uvedeném příkladu, pokud je výzkumník špatný, je doba zotavení kratší nebo rovna 8,2 týdnů. V matematice je to:
H0 μ ≤ 8.2
odmítnutí nulové hypotézy
před deseti nebo tak lety jsme věřili, že ve sluneční soustavě bylo 9 planet. Pluto byl degradován jako planeta v roce 2006. Nulová hypotéza „Pluto je planeta“ byla nahrazena „Pluto není planeta.,“Samozřejmě, odmítnutí nulové hypotézy není vždy tak snadné-tvrdá část obvykle zjišťuje, jaká je vaše nulová hypotéza na prvním místě.
příklady testování hypotéz (Test jednoho vzorku Z)
test jednoho vzorku z se nepoužívá příliš často (protože zřídka známe skutečnou standardní odchylku populace). Je však dobré pochopit, jak to funguje, protože je to jeden z nejjednodušších testů, které můžete provést při testování hypotéz., V anglické třídě máš se naučit základy (jako gramatika a pravopis), než byste mohli napsat článek, že jeden vzorek z testů jako základ pro pochopení složitějších testování hypotéz. Tato stránka obsahuje dva příklady testování hypotéz pro jeden vzorek z-testů.
jeden příklad testování hypotéz: # 2
ředitel určité školy tvrdí, že studenti v jeho škole jsou nadprůměrní inteligence. Náhodný vzorek třiceti studentů IQ skóre mají průměrné skóre 112., Existují dostatečné důkazy na podporu tvrzení ředitele? Průměrné IQ populace je 100 se standardní odchylkou 15.
Krok 1: uveďte nulovou hypotézu. Uznávanou skutečností je, že populační průměr je 100, takže: H0: μ=100.
Krok 2: uveďte alternativní hypotézu. Tvrdí se, že studenti mají nadprůměrné skóre IQ, takže:
H1: μ > 100.
skutečnost, že hledáme skóre „větší než“ určitý bod, znamená, že se jedná o test s jedním ocasem.
Krok 3: nakreslete obrázek, který vám pomůže vizualizovat problém.,
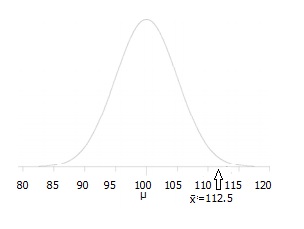
Krok 4: Uveďte úroveň alfa. Pokud nedostanete alfa úroveň, použijte 5% (0,05).
Krok 5: Najděte oblast odmítnutí (danou úrovní alfa výše) z tabulky z. Oblast .05 se rovná z-skóre 1,645.
Krok 6: Najít testovací statistika pomocí tohoto vzorce: 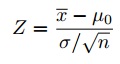
Pro tuto sadu dat: z= (112.5 – 100) / (15/√30) = 4.56.
Krok 6: Pokud je Krok 6 větší než Krok 5, odmítněte nulovou hypotézu., Pokud je to méně než Krok 5, nemůžete odmítnout nulovou hypotézu. V tomto případě je větší (4.56 > 1.645), takže můžete odmítnout null.
jeden příklad testování hypotéz: # 3
hladiny glukózy v krvi u obézních pacientů mají průměr 100 se standardní odchylkou 15. Výzkumník si myslí, že strava s vysokým obsahem surového kukuřičného škrobu bude mít pozitivní nebo negativní vliv na hladinu glukózy v krvi., Vzorek 30 pacientů, kteří vyzkoušeli dietu surového kukuřičného škrobu, má průměrnou hladinu glukózy 140. Otestujte hypotézu, že surový kukuřičný škrob měl účinek.
* tento proces je mnohem jednodušší, pokud používáte TI-83 nebo Excel pro výpočet z-skóre („kritická hodnota“).,
Zobrazit:
- Kritické z hodnoty TI 83
- Z-Skóre v aplikaci Excel
Testování Hypotéz Příklady: Průměr (Pomocí TI 83)
můžete použít TI 83 kalkulačka pro testování hypotéz, ale kalkulačka nebude zjistit nulové a alternativní hypotézy; to je na vás, abyste si přečíst otázku a vstup do kalkulátoru.
příklad problému: vzorek 200 lidí má průměrný věk 21 s populační směrodatnou odchylkou (σ) 5. Otestujte hypotézu, že průměr populace je 18, 9 při α = 0, 05.
Krok 1: uveďte nulovou hypotézu., V tomto případě je nulová hypotéza, že populační průměr je 18,9, takže píšeme:
H0: μ = 18,9
Krok 2: uveďte alternativní hypotézu. Chceme vědět, zda je náš vzorek, který má průměr 21 místo 18.9, opravdu se liší od populace, tedy naši alternativní hypotézu:
H1: μ ≠ 18.9
Krok 3: Stiskněte Stat poté stiskněte šipku doprava dvakrát do vyberte TESTY.
Krok 4: stisknutím 1 Vyberte 1: z-Test…. Stiskněte klávesu ENTER.
Krok 5: pomocí pravé šipky vyberte statistiky.
Krok 6: Zadejte data z problému:
μ0: 18.,9
σ: 5
x: 21
n: 200
μ: μ μ0
Krok 7: šipka dolů pro výpočet a stiskněte klávesu ENTER. Kalkulačka zobrazuje hodnotu p:
p = 2,87 × 10-9
to je menší než naše alfa hodnota.05. To znamená, že bychom měli odmítnout nulovou hypotézu.
Bayesovské testování hypotéz: co to je?
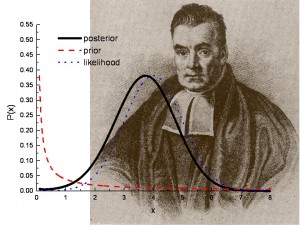
Image: Los Alamos National Lab.
Bayesovské testování hypotéz pomáhá odpovědět na otázku: Mohou se výsledky testu nebo průzkumu opakovat?
proč nám záleží na tom, zda se test může opakovat?, Řekněme, že dvacet lidí ve stejné vesnici přišlo s leukémií. Skupina vědců zjistila, že na vině jsou věže mobilních telefonů. Druhá studie však zjistila, že věže mobilních telefonů nemají nic společného s rakovinovým klastrem v obci. Ve skutečnosti zjistili, že rakoviny byly zcela náhodné. Pokud to zní nemožné, ve skutečnosti se to může stát! Shluky rakoviny se mohou stát jednoduše náhodou. Mohlo by existovat mnoho důvodů, proč byla první studie vadná., Jedním z hlavních důvodů může být to, že prostě nebrali v úvahu, že se někdy věci dějí náhodně a my prostě nevíme proč.
hodnoty P.
je dobré dát lidem vědět, zda jsou vaše studijní výsledky solidní nebo zda se mohly stát náhodou. Obvyklým způsobem, jak toho dosáhnout, je otestovat své výsledky s hodnotou p. Hodnota p je číslo, které získáte spuštěním testu hypotézy na vašich datech. Hodnota P 0,05 (5%) nebo méně obvykle stačí k tvrzení, že vaše výsledky jsou opakovatelné., Existuje však i jiný způsob, jak otestovat platnost vašich výsledků: Bayesovské testování hypotéz. Tento typ testování vám dává další způsob, jak otestovat sílu vašich výsledků.
Bayesovské testování hypotéz.
tradiční testování (typ, na který jste pravděpodobně narazili v elementárních statistikách nebo statistikách AP) se nazývá non-Bayesian. To je, jak často výsledek se stane přes opakované běhy experimentu. Je to objektivní pohled na to, zda je experiment opakovatelný.testování Bayesovské hypotézy je subjektivní pohled na totéž., Bere v úvahu, kolik víry máte ve svých výsledcích. Jinými slovy, vsadili byste peníze na výsledek svého experimentu?
rozdíly mezi tradičním a Bayesovským testováním hypotéz.
tradiční testování (Non Bayesian) vyžaduje opakování odběru vzorků znovu a znovu, zatímco Bayesovské testování ne. Hlavní rozdíl mezi těmito dvěma je v prvním kroku testování: uvedení pravděpodobnostního modelu. V Bayesian testování přidáte předchozí znalosti k tomuto kroku., Vyžaduje také použití zadní pravděpodobnosti, což je podmíněná pravděpodobnost daná náhodné události po zvážení všech důkazů.
argumenty pro Bayesovské testování.
mnoho vědců si myslí, že je lepší alternativou k tradičnímu testování, protože:
- zahrnuje předchozí znalosti o datech.
- bere v úvahu osobní přesvědčení o výsledcích.
argumenty proti.
- včetně předchozích údajů nebo znalostí není opodstatněné.
- je obtížné vypočítat ve srovnání s non-Bayesovským testováním.,
Zpět na začátek
Testování Hypotéz Články
Základy
- Co je Ad Hoc Testování?
- Test kompozitní hypotézy
- co je oblast odmítnutí?
- co je to test se dvěma ocasy?
- jak se rozhodnout, zda test hypotézy je test s jedním ocasem nebo Test s dvěma ocasy.
- jak se rozhodnout, zda je hypotéza test s levým ocasem nebo test s pravým ocasem.
- jak uvést nulovou hypotézu ve statistice.
- jak najít kritickou hodnotu.
- jak podpořit nebo odmítnout nulovou hypotézu.,
specifické testy:
- ANOVA.
- Brunner Munzel Test (Zobecněný Wilcoxonův Test)
- Chi Square Test Normality
- Cochran-Mantel-Haenszel Test
- F-Test
- Granger Kauzality Test.
- Hotellingův Test T-Squared
- KPSS.
- jaký je Test pravděpodobnosti a poměru?
- Log rank test.
- MANCOVA
- sekvenční test pravděpodobnosti
- jak spustit Sign Test.
- T Test: jeden vzorek.
- T-Test: dva vzorky.
- Welch ‚ s ANOVA.
- Welchův Test na nerovné odchylky.,
- z-Test: jeden vzorek.
- z Test: dva proporce
- Wald Test.
- co je to akceptační oblast?
- Jak vypočítat Chebyshevovu větu.
- rozhodovací pravidlo.
- stupně volnosti.
- Directional Test
- false Discovery Rate
- jak vypočítat nejméně významný rozdíl.
- úrovně ve statistice.
- Jak vypočítat rozpětí chyby.
- Střední rozdíl (rozdíl v prostředcích)
- problém s vícenásobným testováním.
- co je Neyman-Pearson Lemma?
- jeden vzorek Střední Test.,
- REGWF
- jak najít velikost vzorku (obecné pokyny).
- Sig 2 (Tailed) což znamená ve výsledcích
- co je standardizovaná Statistika testů?
- jak najít standardní chybu
- standardizované hodnoty: Příklad.
- Jak vypočítat T-skóre.
- T-skóre vs. Z.skóre.
- testování jediného průměru.
- nerovnoměrné velikosti vzorku.
- jednotně nejsilnější testy.
- Jak vypočítat Z-skóre.
——————————————————————————
Potřebujete pomoci s úkoly nebo zkoušky otázka?, S Chegg studie, můžete získat krok za krokem řešení vašich otázek od odborníka v oboru. Vaše první 30 minut s Chegg tutor je zdarma!