Kumulativní četnost

• Příklad 1 – Diskrétní proměnné
• Příklad 2 – Spojité proměnné
• Další kumulativní četnost výpočtů

Kumulativní frekvence se používá k určení počtu pozorování, které leží nad (nebo pod) konkrétní hodnotu v datové sadě. Kumulativní frekvence se vypočítá pomocí tabulky rozložení frekvence, která může být vytvořena z kmenových a listových pozemků nebo přímo z dat.

kumulativní frekvence se vypočítá přidáním každé frekvence z tabulky distribuce frekvence do součtu jejích předchůdců., Poslední hodnota bude vždy rovna součtu všech pozorování, protože všechny frekvence budou již přidány k předchozímu součtu.

diskrétní nebo spojité proměnné

proměnné v jakémkoli výpočtu lze charakterizovat hodnotou, která jim byla přiřazena. Diskrétní proměnná se skládá ze samostatných nedělitelných kategorií. Mezi proměnnou a jejím sousedem nemohou existovat žádné hodnoty. Například, pokud byste měli sledovat třídní docházku registrovanou ze dne na den, můžete zjistit, že třída má 29 studentů na jeden den a 30 studentů na jiném., Není však možné, aby docházka studentů byla mezi 29 a 30 lety. (Mezi těmito dvěma hodnotami prostě není prostor pozorovat žádné hodnoty, protože neexistuje způsob, jak mít 29 a půl studentů.)

ne všechny proměnné jsou charakterizovány jako diskrétní. Některé proměnné (jako je čas, výška a hmotnost) nejsou omezeny na pevnou sadu nedělitelných kategorií. Tyto proměnné se nazývají spojité proměnné a jsou dělitelné do nekonečného počtu možných hodnot. Například čas lze měřit ve zlomkových částech hodin, minut, sekund a milisekund., Takže místo dokončení závodu za 11 nebo 12 minut může žokej a jeho kůň překročit cílovou čáru za 11 minut a 43 sekund.

je nezbytné znát rozdíl mezi těmito dvěma typy proměnných, aby bylo možné správně vypočítat jejich kumulativní frekvenci.

Příklad 1-diskrétní proměnné

celkový počet horolezců Lake Louise, Alberta byl zaznamenán během 30denního období. Výsledky jsou následující:

31, 49, 19, 62, 24, 45, 23, 51, 55, 60, 40, 35 54, 26, 57, 37, 43, 65, 18, 41, 50, 56, 4, 54, 39, 52, 35, 51, 63, 42.,e diskrétní proměnné:

• nastavit stonek a list děj, (viz oddíl stonku a listů pozemků) s další sloupce označené Frekvence, Maximální Hodnota a Kumulativní frekvence
• zjistit četnost pozorování pro každé kmenové
• najít horní hodnota u každé kmenové
• vypočítat kumulativní četnost přidáním čísla v Frekvence sloupce
• zaznamenejte všechny výsledky v grafu

vytvoření grafu pomocí y-osy (nebo svislé čáry) pro kumulativní frekvence a osa x (nebo horizontální linku) na počtu lidí, kteří horolezectví.,

odpovědi:

1. počet horolezců se pohybuje od 4 do 65. Za účelem vytvoření stopky a listu jsou data nejlépe seskupena do třídních intervalů 10.

   každý interval může být umístěn ve sloupci stonku. Čísla v tomto sloupci představují první číslo v intervalu třídy. (Například stonek 0 představuje interval 0-9, stonek 1 představuje interval 10-19 a tak dále.)

   sloupec listů uvádí počet pozorování, která leží v každém intervalu třídy., Například v Stem 2 (interval 20-29) jsou tři pozorování, 23, 24 a 26, reprezentována jako 3, 4 a 6.

   frekvenční sloupec uvádí počet pozorování nalezených v intervalu třídy. Například u stonku 5 bylo nalezeno devět listů (nebo pozorování); v stonku 1 jsou pouze dva.

   použijte frekvenční sloupec pro výpočet kumulativní frekvence.

   • nejprve přidejte číslo ze sloupce frekvence ke svému předchůdci. Například v Stem 0 máme pouze jedno pozorování a žádné předchůdce. Kumulativní frekvence je jedna.,
     1 + 0 = 1
   • v kmeni 1 však existují dvě pozorování. Přidejte tyto dva na předchozí kumulativní frekvenci (jednu) a výsledek je tři.
     1 + 2 = 3
   • ve Stem 2 Existují tři pozorování. Přidejte tyto tři k předchozí kumulativní frekvenci (tři) a celková (šest) je kumulativní frekvence pro Stem 2.
     3 + 3 = 6
   • pokračujte v těchto výpočtech, dokud nepřidáte všechna čísla ve sloupci frekvence.
   • zaznamenejte výsledky ve sloupci kumulativní frekvence.,

   sloupec horní hodnoty uvádí pozorování (proměnnou) s nejvyšší hodnotou v každém intervalu třídy. Například ve Stem 1 představují dvě pozorování 8 a 9 proměnné 18 a 19. Horní hodnota těchto dvou proměnných je 19.

   Tabulka 1.,>8 9

   
   

   2	19	1 + 2 = 3
   2	3 4 6	3	26	3 + 3 = 6
   3	1 5 5 7 9	5	39	6 + 5 = 11
   4	0 1 2 3 5 9	6	49	11 + 6 = 17
   5	0 1 1 2 4 4 5 6 7	9	57	17 + 9 = 26
   6	0 2 3 5	4	65	26 + 4 = 30

2. Since these variables are discrete, use the upper values in plotting the graph., Vykreslete body a vytvořte souvislou křivku nazvanou ogive.

   vždy označte graf kumulativní frekvencí-odpovídající počtu pozorování-na svislé ose.,bel vodorovné ose s jinou proměnnou (v tomto případě, celkové horolezec se počítá), jak je uvedeno níže:

   

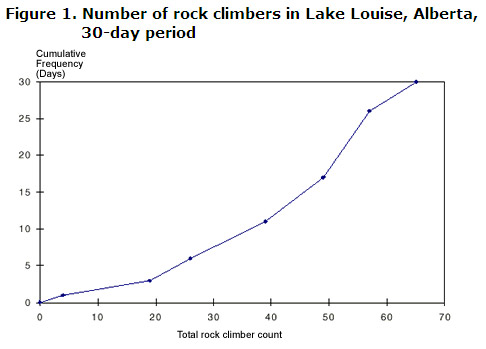
následující informace mohou být získány buď z grafu, nebo v tabulce:

• na 11 30 dnů, 39 lidí nebo méně, vylezl na skály kolem Lake Louise
• na 13 30 dní, 50 nebo více lidí, vylezl na skály kolem Lake Louise

Při kontinuální proměnná se používá, jak výpočet kumulativní četnosti a vykreslování grafu vyžadují trochu jiný přístup, než který se používá pro diskrétní proměnné.,

Příklad 2 – Spojité proměnné

Za 25 dní, hloubku sněhu na Whistler Mountain, B. C. byla měřena (na celé centimetry) a zaznamenal takto:

242, 228, 217, 209, 253, 239, 266, 242, 251, 240, 223, 219, 246, 260, 258, 225, 234, 230, 249, 245, 254, 243, 235, 231, 257.,

1. Použití spojitých proměnných výše:
   • nastavit frekvenci tabulky
   • najít četnosti pro každý interval
   • vyhledejte koncový bod pro každou třídu interval
   • vypočítat kumulativní četnost přidáním čísla v Frekvence sloupce
   • všechny výsledky v tabulce
2. Použít informace získané z frekvenční tabulky rozložení na pozemku kumulativní četnost graf.

odpovědi:

1. měření hloubky sněhu se pohybuje od 209 cm do 266 cm., Za účelem vytvoření tabulky rozložení frekvence jsou data nejlépe seskupena do třídních intervalů po 10 cm.

   ve sloupci hloubky sněhu je uveden každý interval třídy 10 cm od 200 cm do 270 cm.

   frekvenční sloupec zaznamenává počet pozorování, která spadají do určitého intervalu. Tento sloupec představuje pozorování ve sloupci Tally, pouze v číselné podobě.,

   Do Koncového bodu, sloupce, funkce, stejně jako Horní hodnota sloupec Cvičení 1, s tou výjimkou, že koncový bod je nejvyšší číslo v intervalu, bez ohledu na skutečnou hodnotu každého pozorování. Například v intervalu třídy 210-220 je skutečná hodnota obou pozorování 217 a 219. Místo použití 219 se však používá koncový bod 220.

   kumulativní frekvenční sloupec uvádí součet každé frekvence přidané ke svému předchůdci.

   Tabulka 2. Hloubka sněhu měřená na Whistler Mountain, B. C.,e2cd5a9″>

   
   

   5	240	11
   240 to < 250		7	250	18
   250 to < 260		5	260	23
   260 to < 270		2	270	25

2. Because the variable is continuous, the endpoints of each class interval are used in plotting the graph., Vynesené body jsou spojeny a tvoří ogive.

   vzpomeňte si, kumulativní četnost (počet pozorování) je označen na svislé ose y a nějaké jiné proměnné (hloubka sněhu) je uvedena na horizontální ose x, jak je znázorněno na Obrázku 2.,

   

následující informace mohou být získány buď z grafu, nebo v tabulce:

• žádná z 25 dnů měl hloubku sněhu méně než 200 cm
• jeden z 25 dní sníh měl hloubku menší než 210 cm
• dva z 25 dní sníh měl hloubku 260 cm nebo více

Další kumulativní četnost výpočtů

Další výpočet, který lze získat pomocí frekvenční distribuce je tabulka relativní četnosti rozložení. Tato metoda je definována jako procento pozorování klesajících v každém intervalu třídy., Relativní kumulativní frekvenci lze nalézt vydělením frekvence každého intervalu celkovým počtem pozorování. (Další informace naleznete v kapitole distribuce kmitočtů s názvem organizace dat.)

tabulka rozložení frekvence může být také použita pro výpočet kumulativního procenta. Tato metoda distribuce frekvence nám dává procento kumulativní frekvence, na rozdíl od procenta pouze frekvence.